代码随想录21 530.二叉搜索树的最小绝对差 | 501.二叉搜索树中的众数 | 236. 二叉树的最近公共祖先
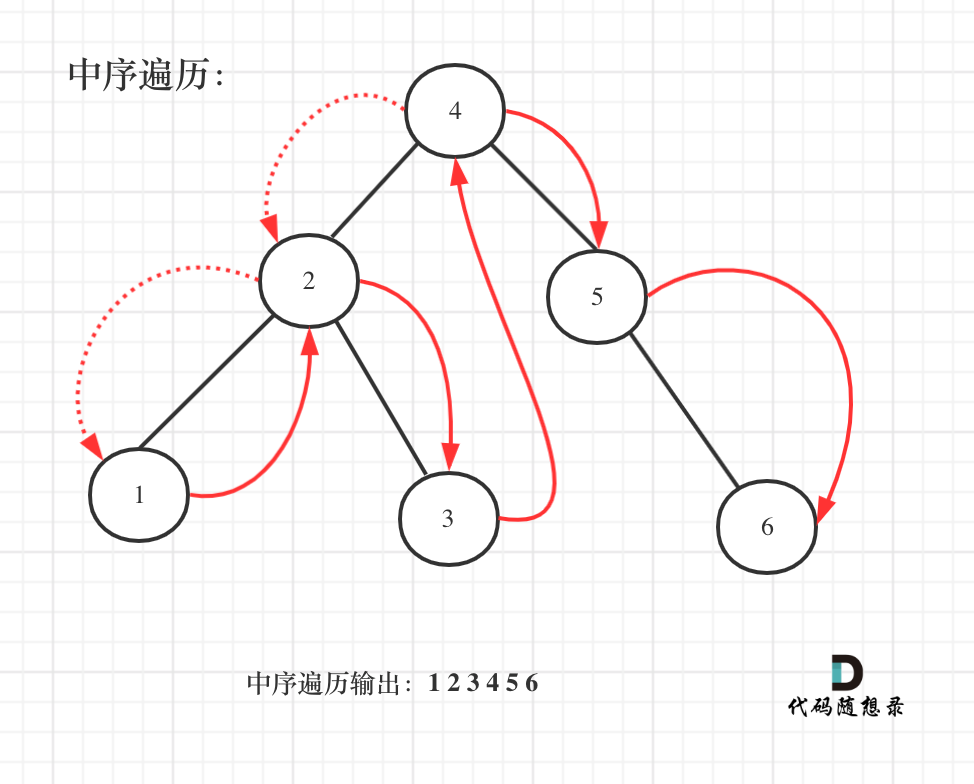
530. 二叉搜索树的最小绝对差
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
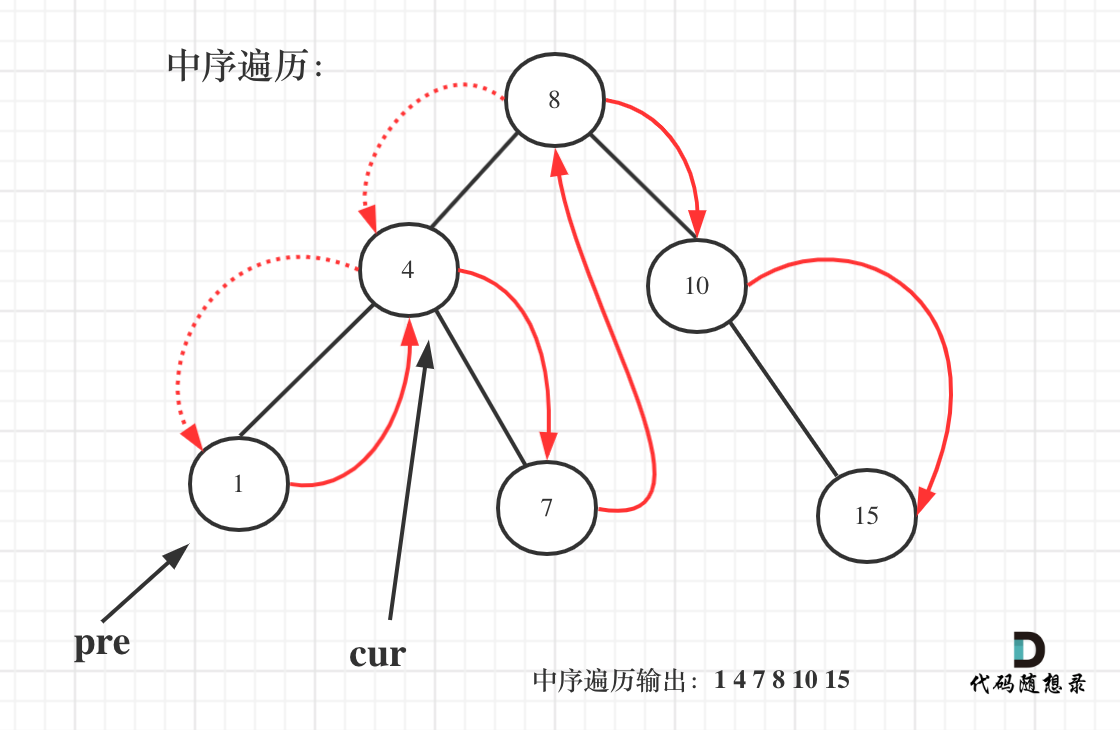
class Solution {
TreeNode pre;
int result = Integer.MAX_VALUE;
public int getMinimumDifference(TreeNode root) {
if (root == null) return 0;
helper(root);
return result;
}
private void helper(TreeNode root) {
if (root == null) return;
helper(root.left);
if (pre != null) {
result = Math.min(result, root.val - pre.val);
}
pre = root;
helper(root.right);
}
}
501. 二叉搜索树中的众数
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
class Solution { public int[] findMode(TreeNode root) { Map<Integer, Integer> map = new HashMap<>(); List<Integer> list = new ArrayList<>(); if (root == null) return list.stream().mapToInt(Integer::intValue).toArray(); searchBST(root, map); List<Map.Entry<Integer, Integer>> mapList = map.entrySet().stream().sorted((c1, c2) -> c2.getValue().compareTo(c1.getValue())).collect(Collectors.toList()); list.add(mapList.get(0).getKey()); for (int i = 1; i < mapList.size(); i++) { if (mapList.get(i).getValue() == mapList.get(i - 1).getValue()) { list.add(mapList.get(i).getKey()); } else { break; } } return list.stream().mapToInt(Integer::intValue).toArray(); } void searchBST(TreeNode cur, Map<Integer, Integer> map) { if (cur == null) return; map.put(cur.val, map.getOrDefault(cur.val, 0) + 1); searchBST(cur.left, map); searchBST(cur.right, map); } }
236. 二叉树的最近公共祖先
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。

输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3
class Solution { public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) { if (root == null || root == p || root == q) { return root; } TreeNode left = lowestCommonAncestor(root.left, p, q); TreeNode right = lowestCommonAncestor(root.right, p, q); if (left != null && right != null) return root; return left == null ? right : left; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号