代码随想录算法训练营Day6 | | 242.有效的字母异位词 ,349. 两个数组的交集 , 202. 快乐数 ,1. 两数之和

前置知识复习

哈希表

 

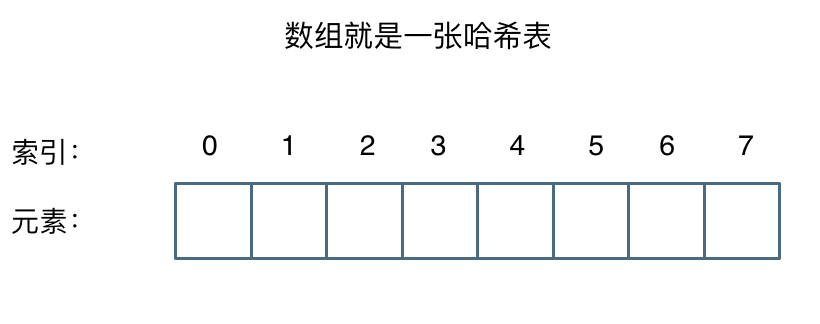
哈希函数

 

哈希碰撞

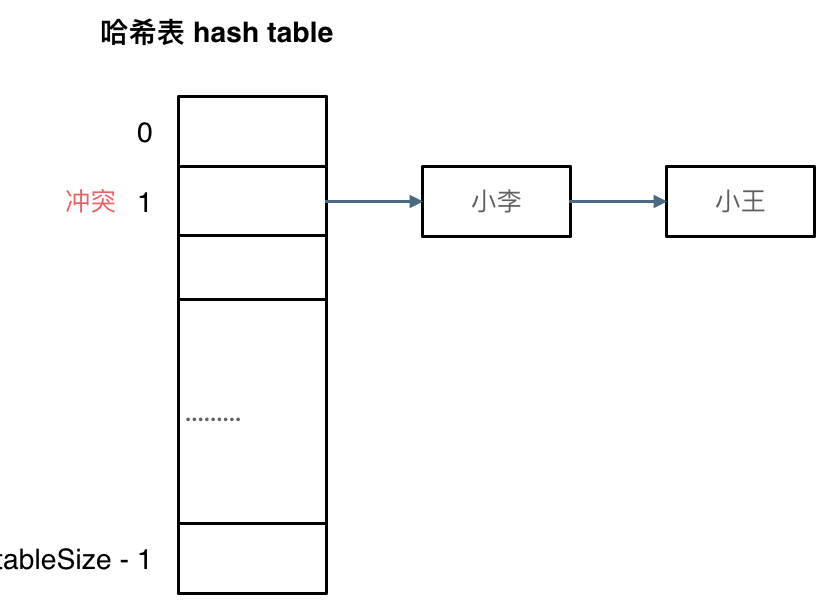
拉链法

  链法就是要选择适当的哈希表的大小，这样既不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间。

  

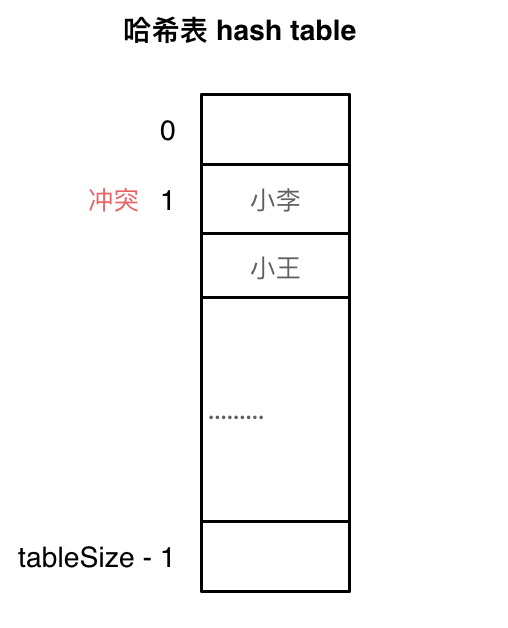
线性探测法

  一定要保证tableSize大于dataSize。 我们需要依靠哈希表中的空位来解决碰撞问题。

 

例题

242. 有效的字母异位词

给定两个字符串 s 和 t ，编写一个函数来判断 t 是否是 s 的字母异位词。

注意：若 s 和 t 中每个字符出现的次数都相同，则称 s 和 t 互为字母异位词。

示例 1:

输入: s = "anagram", t = "nagaram"
输出: true

算法
将s中包含字符的频率存在hashtable中，然后遍历t 如果最终hashtable对应值全是零说明匹配上了 反之则不然

class Solution {
    public boolean isAnagram(String s, String t) {
        int[] cnt = new int[26];
        for (char c : s.toCharArray()) {
            cnt[c - 'a']++;
        }
        for (char c1 : t.toCharArray()) {
            cnt[c1 - 'a']--;
        }

        for (int c : cnt) {
            if (c != 0) {
                return false;
            }
        }
        return true;
    }
}

给定两个数组 nums1 和 nums2 ，返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]
比较简单不赘述了

class Solution {
    public int[] intersection(int[] nums1, int[] nums2) {
        Set<Integer> set1 = new HashSet<>();
        Set<Integer> set2 = new HashSet<>();

        for (int num : nums1) {
            set1.add(num);
        }
        for (int num1 : nums2) {
            if (set1.contains(num1)) {
                set2.add(num1);
            }
        }
        return set2.stream().mapToInt(x -> x).toArray();
    }
}

202. 快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

算法 模拟题 计算出happy数 while loop  n / 10 n % 10 + n % 10 set去个重

 

class Solution {
    public boolean isHappy(int n) {
        HashSet<Integer> set = new HashSet<>();
        while (n!=1){
            if (set.contains(n)) {
                return false;
            } else {
                set.add(n);
                n = this.generateHappyNumber(n);
            }
        }
        return true;
    }

    private int generateHappyNumber(int n) {
        int sum = 0;
        while (n != 0) {
            sum += (n % 10) * (n % 10);
            n /= 10;
        } 
        return sum;
    }
}

two sum

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target  的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。
经典问题 扫一遍 map key -> nums[i] value -> i

class Solution {
    public int[] twoSum(int[] nums, int target) {
        int[] res = new int[]{-1, -1};
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            if (map.containsKey(target - nums[i])) {
                return new int[]{map.get(target - nums[i]), i};
            }
            map.put(nums[i], i);
        }
        return res;
    }
}