【算法4】3.3.红黑树
平衡查找树
理想情况下,我们希望能够保持二分查找树的平衡性。
在一棵含有 N 个结点的树中,我们希望树高为 \(log_2 N\)。
2-3 树
2-3 树由两种结点组成:
- 2- 结点:有一个键和两条链接
- 3- 结点:有两个键和三条链接
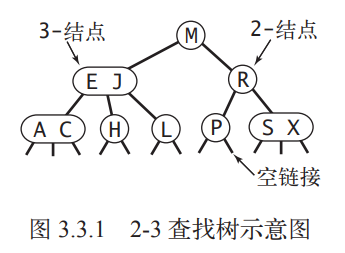
向一棵 2-3 树插入一个键值对:
- 如果查找结束于一个 2- 结点,那么直接将键值对插入该结点形成一个 3- 结点即可
- 如果查找结束于一个 3- 结点,那么需要临时构造一个 4- 结点,再将中键推入父节点。递归此过程直到遇到一个 2- 结点(树的高度不变)或分解根结点(树高度 +1)
红黑树
虽然 2-3 树能够在动态插入保持平衡性,但其直接实现需要维护两种类型的结点、
在不同类型结点间进行转换和复制信息、在结点中对每个键进行比较等,这会增加代码的复杂度和开销。
红黑树是一棵二叉查找树,它使用红色左连接及其连接的两个结点来表示 2-3 树的 3- 结点。

红黑树的另一种定义是含有红黑连接并满足以下条件的二叉查找树:
- 红色连接均为左连接
- 没有任何一个结点同时和两条红连接相连
- 该树是完美黑色平衡的,即任意空链接到根结点的路径上的黑链数量相同
红黑树实现
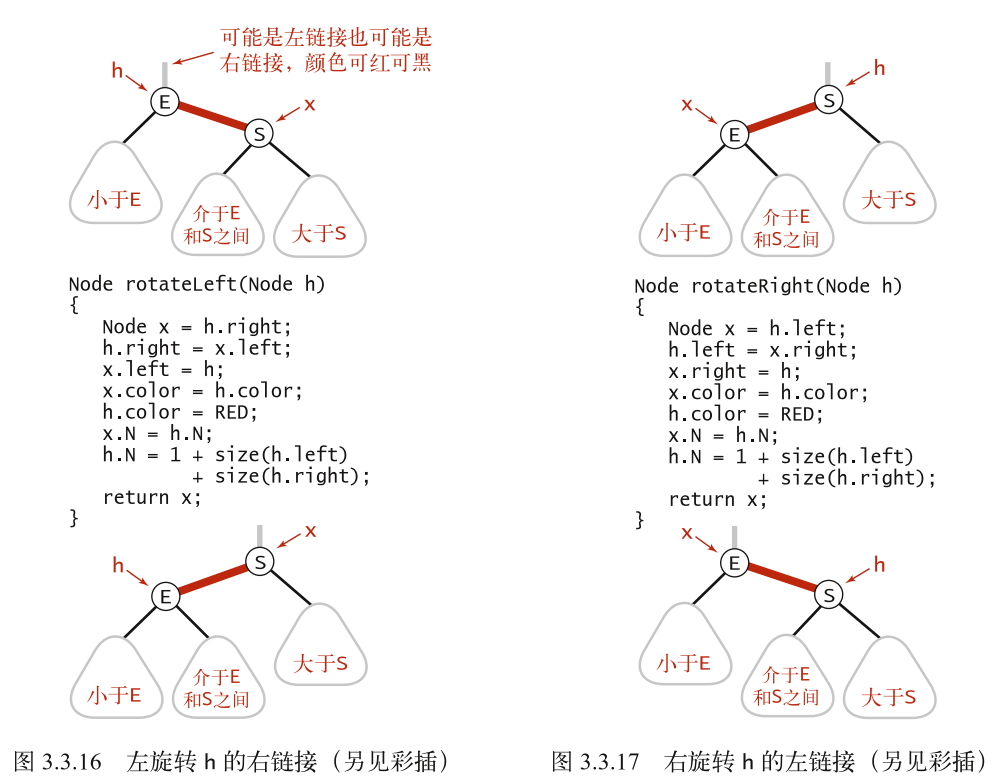
旋转和颜色变换
左旋转:将带有红色右连接的根结点转变成带有红色左连接的根结点
右旋转:将带有红色左连接的根结点转变成带有红色右连接的根结点
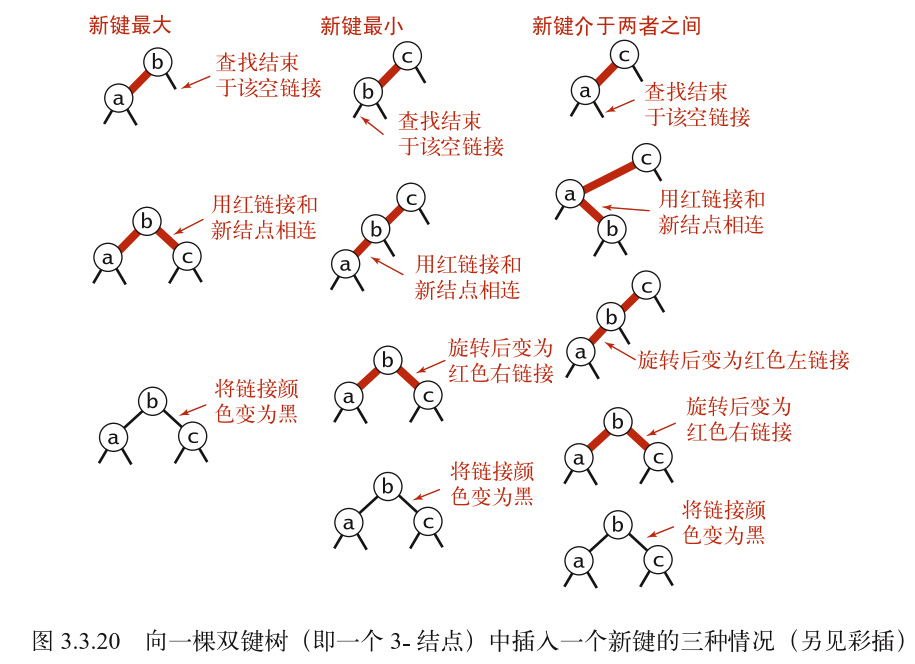
插入新结点时,我们总是使用红色连接将新结点与父结点连接。
向一个 2- 结点插入新键:
- 如果插入到左连接,则会直接形成一个 3- 结点
- 如果插入到右连接,则需要先进行左旋转才会形成一个正确的 3- 结点
向一个 3- 结点插入新键:
- 如果新键大于原树中的两个结点,则将新键插入到右连接。此时需要分解此临时的 4- 结点,即将两条红色连接变成黑色并将父结点的连接变成红色(对应到 2-3 将中键推入父结点并生成两个 2- 子结点)。
- 如果新键小于原树中的两个结点,则将新键连接到左子结点的左连接。此时会出现两条连续的红连接,需要对上层连接进行右旋转,得到第一种情况
- 如果新键介于原树种的两个结点,则将新增连接到左子结点的右连接。对下层连接进行左旋转会得到第二种情况
进行颜色变换后,根结点上的连接可能会变成红色,但根结点上不会再有其他结点,每次插入后需要将根结点上的连接重置成黑色。
对应到代码实现,查找会结束于一个 2- 结点,我们会用红色左/右连接插入新结点,然后依次执行以下步骤:
- 如果左连接是黑色且右连接是红色,进行左旋转(全红是要进行颜色变换)
- 如果左连接是红色且左子结点的左连接也是红色,进行右旋转
- 如果两个连接都是红色,执行颜色变换
代码实现
结点定义:
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node {
private K key;
private V value;
private boolean color; // 指向该结点连接的颜色
private Node left;
private Node right;
public Node(K key, V value, boolean color) {
this.key = key;
this.value = value;
this.color = color;
}
}
private boolean isRed(Node node) {
if (node == null) return BLACK;
return node.color;
}
旋转和颜色变换:
// 传入指向父结点连接
// 返回父节点,并在调用函数重置指向父结点的连接
// 左旋转:将红色右连接变成红色左连接
private Node rotateLeft(Node h) {
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
x.left.color = RED;
x.N = h.N;
h.N = size(h);
return x;
}
// 右旋转
private Node rotateRight(Node h) {
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
x.right.color = RED;
x.N = h.N;
h.N = size(h);
return x;
}
// 颜色变换
// 左右链表由红变黑,父连接变红
private void flipColors(Node h) {
h.left.color = BLACK;
h.right.color = BLACK;
h.color = RED;
}
private int size(Node node) {
if (node == null) {
return 0;
}
return size(node.left) + size(node.right) + 1;
}
插入算法:
// 插入算法
public void put(K key, V value) {
root = put(root, key, value);
root.color = BLACK;
}
private Node put(Node node, K key, V value) {
if (node == null) {
return new Node(key, value, 1, RED);
}
int cmp = node.key.compareTo(key);
if (cmp < 0) {
node.left = put(node.left, key, value);
} else if (cmp > 0){
node.right = put(node.right, key, value);
} else {
node.value = value;
}
if (!isRed(node.left) && isRed(node.right)) node = rotateLeft(node);
if (isRed(node.left) && isRed(node.left.left)) node = rotateRight(node);
if (isRed(node.left) && isRed(node.right)) flipColors(node);
node.N = size(node);
return node;
}



