博客作业--图
1.学习总结(2分)
1.1图的思维导图
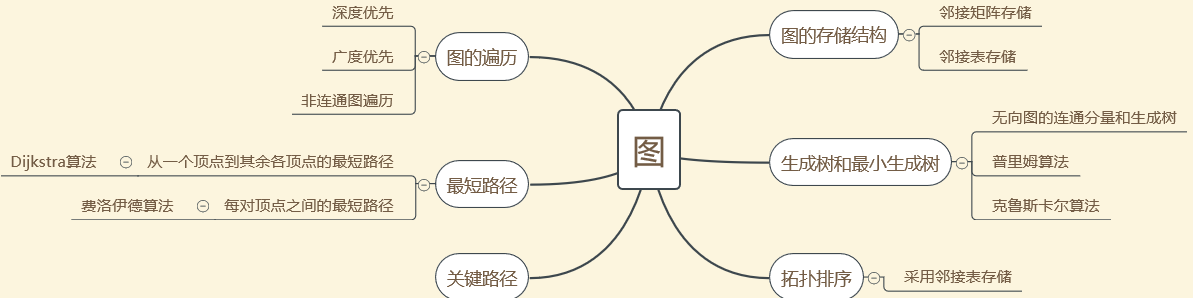
1.2 图结构学习体会
对于图的存储结构包括邻接表和邻接矩阵能够掌握,图的基本运算能够理解但是对于代码的实现还有欠缺,其他的运算包括最短路径和拓扑排序还是比较不懂。在运用图这种数据结构解决一些综合应用问题时还是比较棘手。
2.PTA实验作业(4分)
2.1 题目1:图着色问题
2.2 设计思路(伪代码或流程图)
- 使用回溯法将visited数组初始化为0;
- k=0;
- 依次观察每一种颜色,若顶点之间的着色不冲突则转下一步骤,否则继续搜索
- 若顶点全部着色,输出数组
- 若顶点是一个合法着色,则转处理下一个
- 否则重置顶点颜色
2.3 代码截图

2.4 PTA提交列表说明。
对于图着色时的合法判断语句实现出现不严谨的错误导致答案错误。
2.1 题目2:公路村村通
2.2 设计思路(伪代码或流程图)
- 用最小生成树来求解问题
- 由输入数据建立带权的无向图
- 建立边集
- 采用直接插入排序按权值递增排序
- 生成边数小于n时循环
- 当两顶点属于不同集合,该边是最小生成树
2.3 代码截图

2.4 PTA提交列表说明

本题主要参考了网上的代码,对于最小生成树的运用方法有些欠缺。
2.1 题目3:六度空间
2.2 设计思路
- 对图进行广度优先搜索
- 计算六度空间的个数
- 计算层数,等于6时跳出
- 得出每层中的顶点数
- 计算百分比
2.3 代码截图
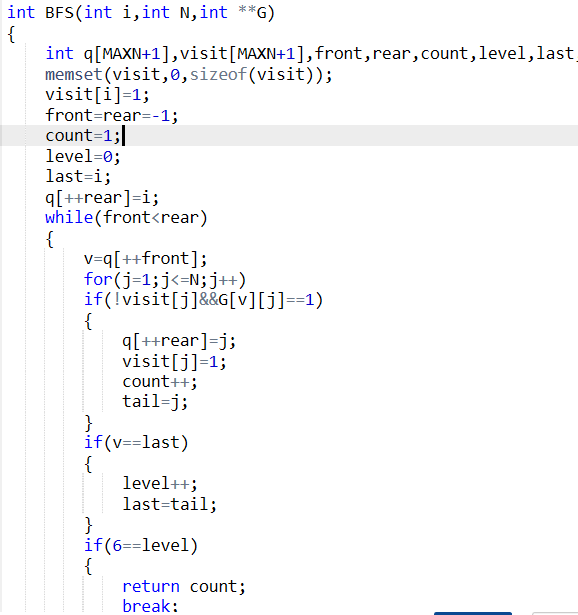
2.4 PTA提交列表说明

在进行图的广度搜索时判断条件出错导致程序错误,以及题目输出条件没看清楚导致错误。
3.截图本周题目集的PTA最后排名

3.2 我的总分:2.5
4. 阅读代码
#include <stdio.h>
#include <stdlib.h>
#define MAXN 10
#define INF = 1000
typedef struct struct_graph{
char vexs[MAXN];
int vexnum;//顶点数
int edgnum;//边数
int matirx[MAXN][MAXN];//邻接矩阵
} Graph;
int pathmatirx[MAXN][MAXN];//记录对应点的最小路径的前驱点,例如p(1,3) = 2 说明顶点1到顶点3的最小路径要经过2
int shortPath[MAXN][MAXN];//记录顶点间的最小路径值
void short_path_floyd(Graph G, int P[MAXN][MAXN], int D[MAXN][MAXN]){
int v, w, k;
//初始化floyd算法的两个矩阵
for(v = 0; v < G.vexnum; v++){
for(w = 0; w < G.vexnum; w++){
D[v][w] = G.matirx[v][w];
P[v][w] = w;
}
}
//这里是弗洛伊德算法的核心部分
//k为中间点
for(k = 0; k < G.vexnum; k++){
//v为起点
for(v = 0 ; v < G.vexnum; v++){
//w为终点
for(w =0; w < G.vexnum; w++){
if(D[v][w] > (D[v][k] + D[k][w])){
D[v][w] = D[v][k] + D[k][w];//更新最小路径
P[v][w] = P[v][k];//更新最小路径中间顶点
}
}
}
}
printf("\n初始化的D矩阵\n");
for(v = 0; v < G.vexnum; v++){
for(w = 0; w < G.vexnum; w++){
printf("%d ", D[v][w]);
}
printf("\n");
}
printf("\n初始化的P矩阵\n");
for(v = 0; v < G.vexnum; v++){
for(w = 0; w < G.vexnum; w++){
printf("%d", P[v][w]);
}
printf("\n");
}
v = 0;
w = 3;
//求 0 到 3的最小路径
printf("\n%d -> %d 的最小路径为:%d\n", v, w, D[v][w]);
k = P[v][w];
printf("path: %d", v);//打印起点
while(k != w){
printf("-> %d", k);//打印中间点
k = P[k][w];
}
printf("-> %d\n", w);
}
int main(){
int v, w;
Graph G;
printf("请输入顶点数:\n");
scanf("%d", &G.vexnum);
printf("请输入初始矩阵值:\n");
for(v = 0; v < G.vexnum; v++){
for(w = 0; w < G.vexnum; w++){
scanf("%d", &G.matirx[v][w]);
}
}
printf("\n输入的矩阵值:\n");
for(v = 0; v < G.vexnum; v++){
for(w = 0; w < G.vexnum; w++){
printf("%d ", G.matirx[v][w]);
}
printf("\n");
}
short_path_floyd(G, pathmatirx, shortPath);
}
弗洛伊德(Floyd)算法求图的最短路径
基本思想:
弗洛伊德算法定义了两个二维矩阵:
- 矩阵D记录顶点间的最小路径
例如D[0][3]= 10,说明顶点0 到 3 的最短路径为10; - 矩阵P记录顶点间最小路径中的中转点
例如P[0][3]= 1 说明,0 到 3的最短路径轨迹为:0 -> 1 -> 3。


