647. Palindromic Substrings（马拉车算法）

问题

求一个字符串有多少个回文子串

Input: "abc"
Output: 3
Input: "aaa"
Output: 6

思路和代码（1）——朴素做法

用dp的基本思想“子问题求解”，但是因为没有重叠子问题，没必要用dp数组或者矩阵来存储中间结果。
直接遍历每个字符，然后以该字符为中心向两边扩张来判断是否回文串，是的话就总数加1。
这时要考虑两种情况，一种是以单字符为中心来扩张即aba这种，另一种是以双字符为中心来扩张即abba。
对于每个字符s[i]要遍历两次扩张，一次以s[i]为中心来扩张，一次以s[i]和s[i+1]为中心来扩张。因此需要遍历2n次（n为字符串长度）。又考虑到最后一个字符s[n-1]后面已经没有字符了，不需要考虑以两个字符为中心的情况，所以实际是遍历2n-1次。
可以用两个指针left和right，单字符为中心的扩张时left和right都初始指向s[i]，双字符为中心的扩张时left指向s[i]，right指向s[i+1]。

时间复杂度O(n^2)，空间复杂度O(1)

class Solution(object):
    def countSubstrings(self, s):
        """
        :type s: str
        :rtype: int
        """
        n = len(s)
        res = 0
        for i in range(2*n-1):
            left = i/2
            right = left + i%2
            while(left >= 0 and right < n and s[left]==s[right] ):
                res += 1
                left -= 1
                right += 1
        return res

思路和代码（2）——Manacher算法

使用马拉车算法，算法根据回文串的对称特点利用之前的信息计算，可以在线性时间内找出所有回文串。

“原字符串”转为“#字符串”
前面说了回文串分为单字符中心和双字符中心，为了可以统一按单字符中心处理。首先在原字符中插入字符'#'，例如aaa经过插入处理后得到"#a#a#a#"，这样遍历到第一个a时其实是以a为单字符中心，遍历到第二个#时就是以aa为双字符中心。第一个#和最后一个#的意义在于补全第一个字符和最后一个字符的“回文串身份”，因为单个字符也算回文串。

镜像计算
我们用p[i]表示以i为中心的回文串半径，p[i]初始化为0。正常情况，我们根据扩张的方法来判断半径是否增加。
特殊情况，如果字符s[i]处于某个已知的“以id为中心，以mx为右边界”的回文串中（此时mx > i），我们称这个回文串为id回文串，此时可以利用id为中心对称过去的镜像索引来简化计算，我们称镜像索引为j。然后有两种情况。

如果p[j]<mx-i，说明i的半径没有超出mx的边界而且等于j的半径，此时p[i]=[j]=p[2*id-1]，这个p[i]值是确定的。

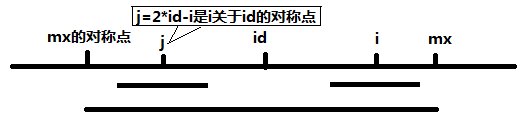
如果p[j]>=mx-i，说明i的半径至少扩张到了mx，mx之后的部分要继续扩张。此时p[i]值不是确定的，但是我们让p[i]=mx-i，因为半径为mx-i是至少的，至于半径是否继续增加取决于mx后面的部分，我们在扩张步骤计算。

简化以上两种情况可以得到：如果mx > i，那么p[i] = min(p[2*id-1], mx-i)

扩张
根据上面的说明，只有在mx >i 以及 p[j] < mx-i的情况下可以通过镜像计算来直接获得半径，其它情况还是要继续扩张。扩张的计算很简单，在当前半径的基础上扩张，判断s[i+p[i]+1]和s[i-p[i]-1]是否相等，相等则半径p[i]加1。

更新id回文串
遍历过程中，如果发现有右边界更大的回文串，则覆盖这个回文串。

“#字符串”的回文个数->“原字符串”的回文个数：
上面计算的半径p[i]会因为#的插入而增多，所以要根据“#字符串”的半径计算一下，得到“原字符串”的半径。我们把所有半径加起来就可以计算出回文字串的数量。

举个双字符为中心的例子，#a#a#，中间#的半径为a#，要转为半径a，2要转为1，直接除以2就得到了。

举个单字符为中心的例子，#a#a#b#a#a#，b的半径#a#a#，要转为半径aa，5要转为2，但是考虑b本身也是一个回文串，实际上是5要转为3，这个时候需要加1之后除以2（这里跟半径的定义有关，我这里的定义中b这个单字符的半径为0。如果定义的b的半径为1，这里的计算就不是加1而是减1了）。

综合来看，直接加1除以2就可以了，因为/会向下取整。

时间复杂度O(n)，空间复杂度O(1)

class Solution(object):
    def countSubstrings(self, s):
        """
        :type s: str
        :rtype: int
        """
        s = '#' + '#'.join(s) + '#'
        n = len(s)
        p = [0]*n
        id = mx = res = 0
        for i in range(1,n-1):
            if(mx > i):
                p[i] = min(mx-i, p[2*id-i])
            while i+p[i]+1 < n and i-p[i]-1 >=0 and s[i+p[i]+1] == s[i-p[i]-1]:
                p[i] += 1
            if(i + p[i] > mx):
                id = i
                mx = i + p[i]
            res += (p[i]+1)/2
        return res