论文笔记:IRGAN——A Minimax Game for Unifying Generative and Discriminative Information
2017 SIGIR
简单介绍
IRGAN将GAN用在信息检索(Information Retrieval)领域,通过GAN的思想将生成检索模型和判别检索模型统一起来,对于生成器采用了基于策略梯度的强化学习来训练,在三种典型的IR任务上(四个数据集)得到了更显著的效果。
生成式和判别式的检索模型
生成式检索模型(query -> document)认为query和document之间存在潜在的生成过程,其缺点在于很难利用其它相关的信息,比如链接数,点击数等document和document之间的相关数据。
判别式检索模型(query+document -> relevance)同时考虑query和document作为特征,预测它们的相关性,其缺点在于缺乏获取有用特征的方法。
GAN
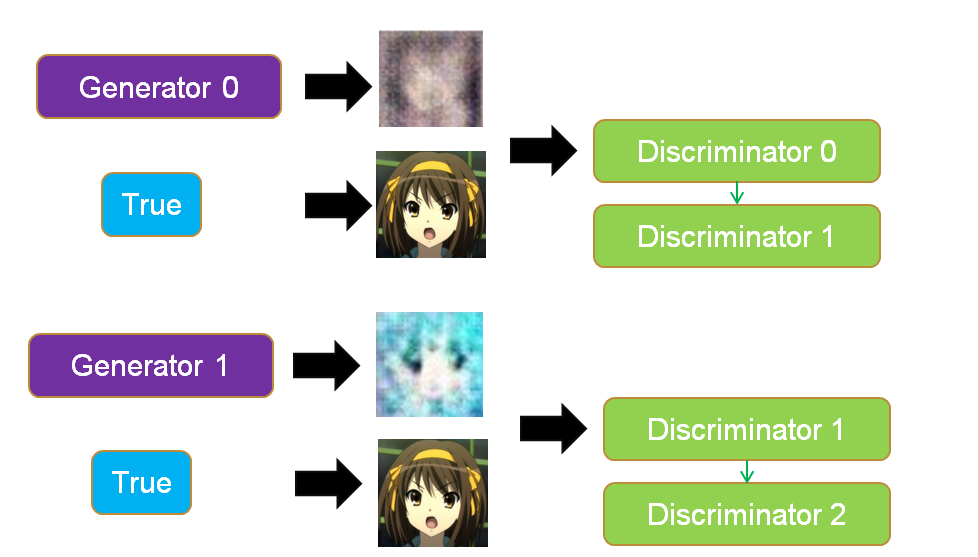
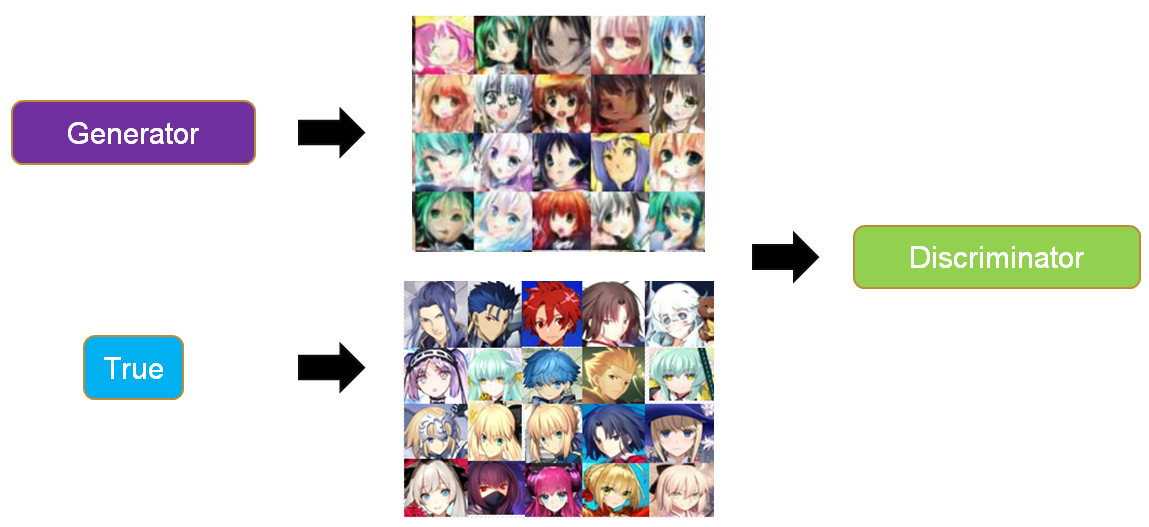
GAN里面的生成器和判别器通过相互博弈来完成工作,举例来说,我们要生成动漫人物头像,如下两个图所示。
- 训练判别器:初代的生成器Generator0会生成很模糊的动漫头像,这个时候我们把Generator0产生的头像作为0标签,真实的头像作为1标签丢入到初代的判别器Discriminator0中训练,得到新一代判别器Discriminator1,这个判别器能够辨认真实头像和Generator0产生的假头像,如果输入是一个真实头像,Discriminator1会输出1,如果输入是一个Generator0生成的头像,Discriminator1会输出0。
- 训练生成器:然后,我们训练Generator0,目标是使得Discriminator1判断生成器生成的头像为真实头像(输出标签为1),以这个为目标训练得到的Generator1能够成功骗过Discriminator1。对于Discriminator1,如果输入是一个Generator1生成的头像,它会输出1。
- 迭代博弈:上面两个步骤就完成了一次博弈,接着会不断迭代这个博弈,Discriminator1会进化成Discriminator2能够成功分辨Generator1产生的是假头像(输出0标签),然后Generator1为了骗过Discriminator2又会进化成Generator2。不断迭代这个过程,最后就能生成一些逼真的动漫人物头像。
IRGAN
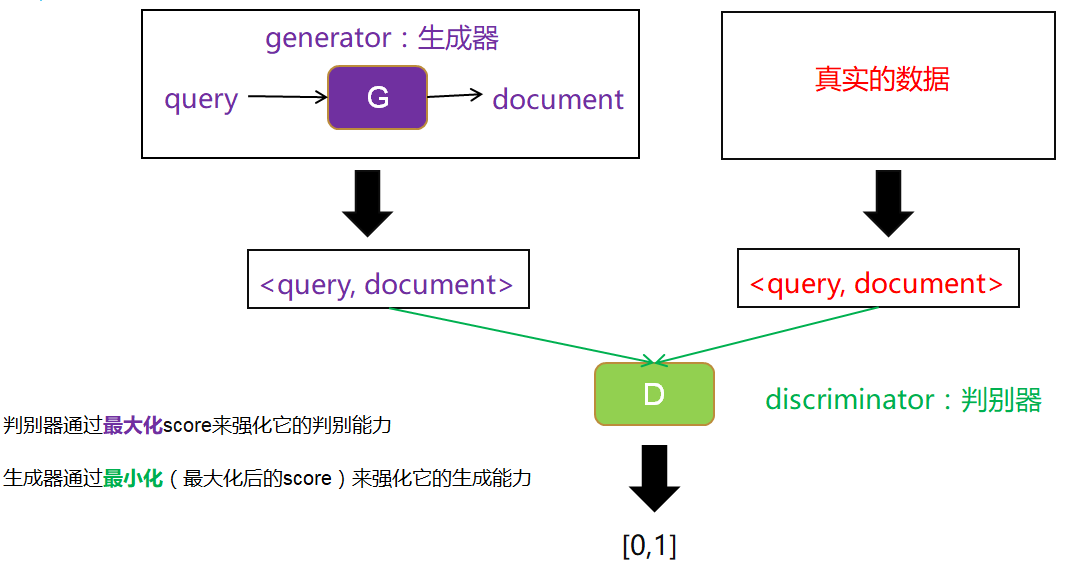
- 可以利用GAN的思想,把两种检索模型结合起来,克服它们的缺点。如下图所示。
- 以生成式检索模型作为生成器,输入query,我们选取相关的document,构成数据对,作为生成数据。
- 以判别式检索模型作为判别器,用一个打分score来表示判别器的判别能力,判别器越能区分生成数据和真实数据(即输入生成数据时输出0,输入真实数据时输出1),则判别能力越强。
- 根据生成器生成的固定数据和真实数据,训练判别器。然后固定判别器,训练生成器使得判别器的判别能力最小化(即输入生成数据时也输出1)。这样完成一次博弈,迭代多次博弈不断训练。
从极大似然法(MLE)到GAN再到IRGAN
- 传统的生成问题:给定一个数据集D,我们构建一个模型,模型产生的数据分布q(x)可以拟合真实的数据分布p(x),我们希望真实的数据在我们学到的模型上有一个很高的概率密度。
- 最小化KL散度:如下式所示,其实这个过程就是在最小化交叉熵。因为真实数据分布不变,信息熵不变,可以看作是在最小化相对熵(KL散度)。这几个熵我在另一篇博文信息熵,交叉熵和相对熵中有介绍。
\[\max_{q} \frac {1}{|D|} \sum_{x \in D} log \ q(x) \approx \max_{q} E_{x \sim q(x)} [log \ q(x)] = \min_q \int_{x} p(x) \ log \frac {1}{q(x)}
\]
- 不对称问题:这样一个广为使用方法有个不对称的问题,对于KL散度,当p(x)>0而q(x)趋近于0时会产生一个高损失,这没有问题,但是当q(x)>0而p(x)趋近于0时候,损失却趋近于0,这与我们的目的不相符。
\[\underbrace{\int_{x} p(x) \ log \frac {1}{q(x)}}_{\text{交叉熵}} - \underbrace{\int_{x} p(x) \ log \frac {1}{p(x)}}_{\text{信息熵}} = \underbrace{\int_{x} p(x) \ log \frac {p(x)}{q(x)})}_{相对熵KL(p||q)}
\]
- 不一致问题:还有一个缺点就是,我们实际做的事情和我们希望的事情并不一致,我们实际做的是让真实的数据在我们学习的模型上有一个很高的概率密度,也就是\(\max_q E_{x \sim p(x)}[log \ q(x)]\)(实际的训练评估中我们通过\(\max_{q} \frac {1}{|D|} \sum_{x \in D} log \ q(x)\) 来approximate这个式子)。但是我们希望做的事情是让生成的数据接近真实数据,也就是生成的数据在真实的分布上有一个很高的概率密度,也就是\(\max_q E_{x \sim q(x)}[log \ p(x)]\),但是这件事情我们是做不到的,因为我们并不知道真实数据的分布,我们没法计算p(x),如果知道真实数据的分布我们就不用做这件事了。当然,q(x)等于p(x)时这两个式子就是一样的。
- GAN:上面提到的一个难点是我们没有办法计算p(x),不知道真实数据的分布长什么样,但是在GAN里面可以构建一个判别器来判别一个数据是真实的还是生成的。同时GAN最小化的不是KL散度,而是JS散度,这就解决了不对称的问题。
- 从MLE到GAN:MLE就是模型已定,参数未知,找出一组参数使得模型产生出观测数据的概率最大。用GAN里面的Generator(可以不局限于特定模型比如高斯分布)可以得到一个general的模型。利用GAN里面的Discriminator可以调整模型使得观测数据的概率最大。
- 从GAN到IRGAN:IRGAN就是把GAN的技术用到信息检索中,IRGAN和GAN的不同点在于IRGAN生成器是输入query然后从已有的document中选取,而GAN是用随机噪音进行生成的。因为IRGAN生成的数据是离散的(需要对documents进行采样),所以需要使用基于策略梯度的强化学习来训练生成器。
公式
- 最小化最大化:前面提到,整个训练就是生成器和判别器博弈的过程,如下图中的式子,先进行一个最大化训练一个判别能力强的判别器,然后做一个最小化来训练一个能骗过判别器的生成器。不断迭代这个过程。
![]()
2. **JS散度**:对式子进行最大化后(训练判别器)得到的这个式子其实是一个JS散度,衡量生成数据和真实数据的分布。然后对JS散度进行最小化(训练生成器)就可以使生成数据逼近真实数据。 
3. **训练判别器**:最大化这个式子,使用sample的方法,发现其实就是一个逻辑回归的二分类问题。 
4. **训练生成器**:因为IRGAN里面最后是从document池中进行采样,可能softmax概率改变一点点,采样的结果并不会产生变化,这样难以进行梯度的传递更新,所以使用基于策略梯度的强化学习来训练。 
5. **目标函数的改进**:训练生成器的时候,考虑到目标函数在一开始下降地比较慢,做了一下修改。于是最后得到的策略梯度也发生了变化,奖赏项变成了判别器输出的log,这也很直观,强化学习要让奖赏越来越大,这里刚好就是让判别器的输出越大越好(接近1,让判别器以为生成的数据是真实的)。后面考虑到log使得训练不稳定,于是把log也去掉了。最后为了让奖赏有正有负,做了一个乘2减1的修正。 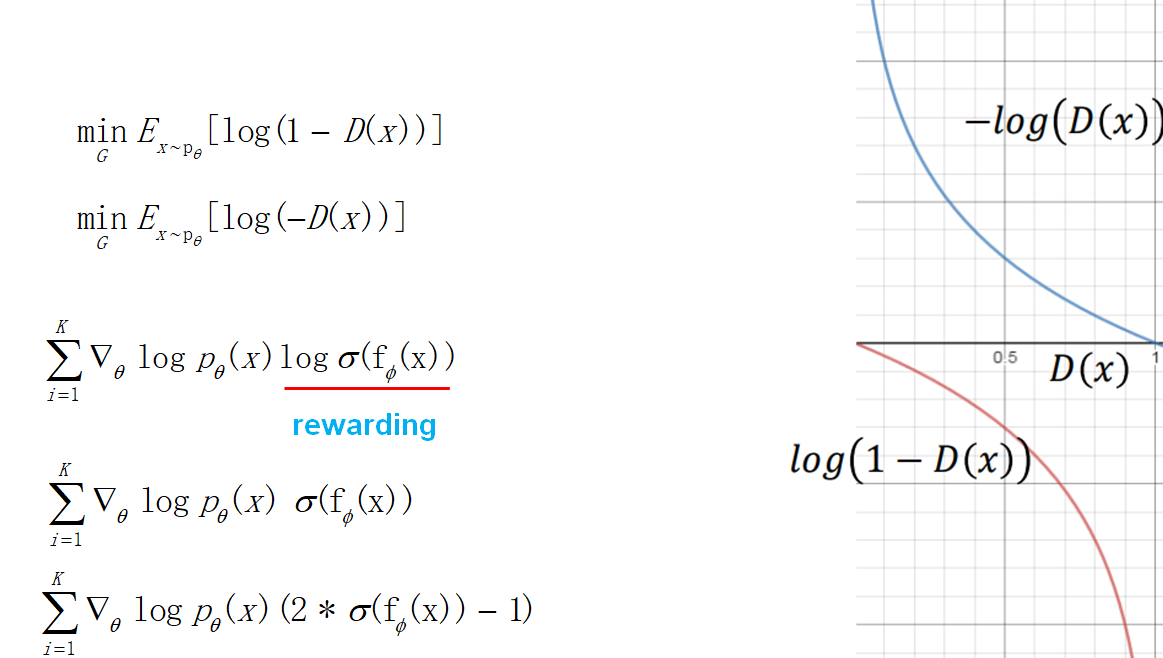
实验
如下几个图所示,其中s(x)表示生成器和判别器的公式。





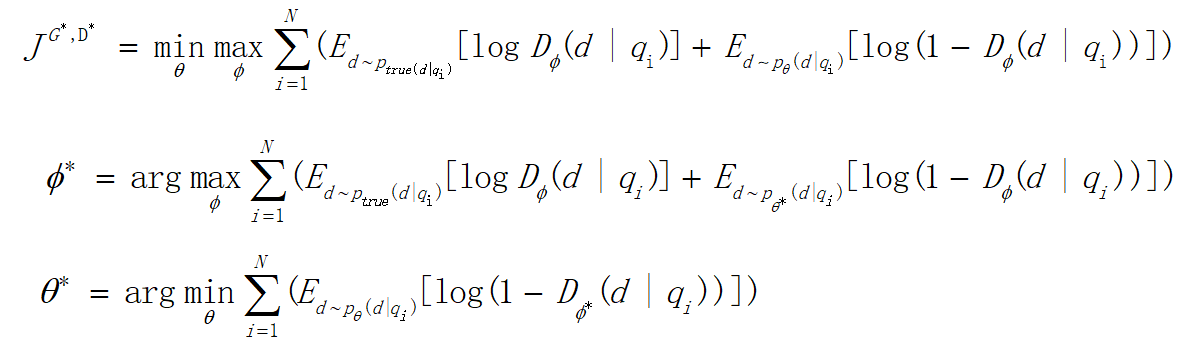

 浙公网安备 33010602011771号
浙公网安备 33010602011771号