论文笔记：多标签学习综述（A review on multi-label learning algorithms）

2014 TKDE(IEEE Transactions on Knowledge and Data Engineering)
张敏灵，周志华

简单介绍
传统监督学习主要是单标签学习，而现实生活中目标样本往往比较复杂，具有多个语义，含有多个标签。本综述主要介绍了多标签学习的一些相关内容，包括相关定义，评价指标，8个多标签学习算法，相关的其它任务。

论文大纲

1. 相关定义：学习任务，三种策略
2. 评价指标：基于样本的评价指标，基于标签的评价指标
3. 学习算法：介绍了8个有代表性的算法，4个基于问题转化的算法和4个基于算法改进的算法
4. 相关任务：多实例学习，有序分类，多任务学习，数据流学习

相关定义

1. 学习任务
   \(X = \mathbb{R}^{d}\)表示d维的输入空间，\(Y=\{y_1, y_2, ..., y_q\}\)表示带有q个可能标签的标签空间。
   训练集$D = {(x^i, y^i)| 1 \leq i \leq m} \(，m表示训练集的大小，上标表示样本序数，有时候会省略。 \)x^i \in X\(，是一个d维的向量。\)y^i \subseteq Y\(，是\)Y\(的一个标签子集。 任务就是要学习一个多标签分类器\)h(\cdot )\(，预测\)h(x) \subseteq Y\(作为x的正确标签集。 常见的做法是学习一个衡量x和y相关性的函数\)f(x, y_j)\(，希望\)f(x, y_{j1}) > f(x, y_{j2})\(，其中\)y_{j1} \in y, y_{j2} \notin y\(。 \)h(x)\(可以由\)f(x)\(衍生得到，\)h(x) = {y_j | f(x,y_j) > t(x), y_j \in Y}\(。 \)t(x)\(扮演阈值函数的角色，把标签空间对分成相关的标签集和不相关的标签集。 阈值函数可以由训练集产生，可以设为常数。当\)f(x, y_j)$返回的是一个概率值时，阈值函数可设为常数0.5。

2. 三种策略
   多标签学习的主要难点在于输出空间的爆炸增长，比如20个标签，输出空间就有\(2^{20}\)，为了应对指数复杂度的标签空间，需要挖掘标签之间的相关性。比方说，一个图像被标注的标签有热带雨林和足球，那么它具有巴西标签的可能性就很高。一个文档被标注为娱乐标签，它就不太可能和政治相关。有效的挖掘标签之间的相关性，是多标签学习成功的关键。根据对相关性挖掘的强弱，可以把多标签算法分为三类。

• 一阶策略：忽略和其它标签的相关性，比如把多标签分解成多个独立的二分类问题（简单高效）。
• 二阶策略：考虑标签之间的成对关联，比如为相关标签和不相关标签排序。
• 高阶策略：考虑多个标签之间的关联，比如对每个标签考虑所有其它标签的影响（效果最优）。

评价指标
可分为两类

• 基于样本的评价指标（先对单个样本评估表现，然后对多个样本取平均）
• 基于标签的评价指标（先考虑单个标签在所有样本上的表现，然后对多个标签取平均）

每类又可分为用于分类任务和用于排序任务的指标，具体指标如下图所示

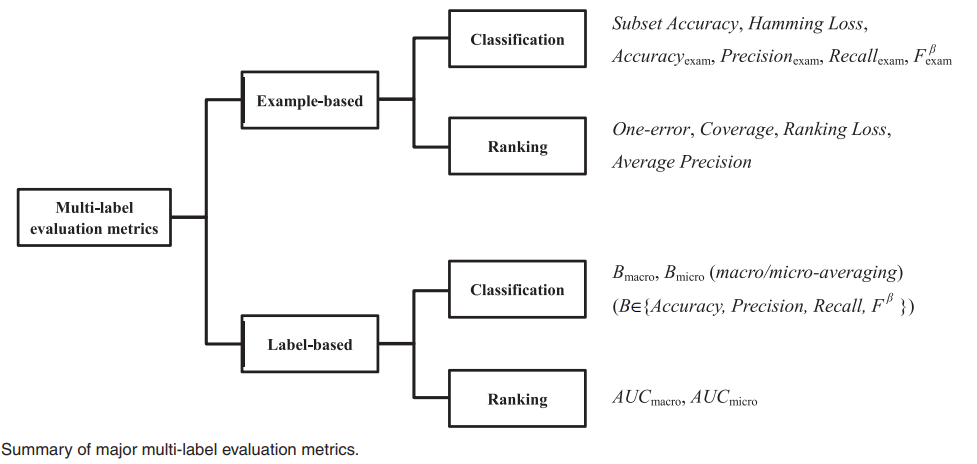
下面对图中的每个指标进行介绍。

基于样本的评价指标

1. Subset Accuracy（衡量正确率，预测的样本集和真实的样本集完全一样才算正确。）

\[\frac{1}{p}\sum_{i=1}^{p} 1\{h(x^i)=y^i\} \]

其中p表示测试集的样本大小，\(1\{\pi\}\)表示\(\pi\)为真时返回1，否则返回0。

2. Hamming Loss（衡量的是错分的标签比例，正确标签没有被预测以及错误标签被预测的标签占比）

\[\frac{1}{p}\sum_{i=1}^{p}\frac{1}{q}\left | h(x^i)\Delta y^i \right | \]

其中\(\Delta\)表示两个集合的对称差，返回只在其中一个集合出现的那些值。

3. Accuracy, Precision, Recall, F值（单标签学习中准确率，精准率，召回率，F值的天然拓展）

\[Accuracy(h) = \frac{1}{p}\sum_{i=1}^{p}\frac{\left | h(x^i)\cap y^i \right |} {\left | h(x^i)\cup y^i \right |} \]

\[Precision(h) = \frac{1}{p}\sum_{i=1}^{p}\frac{\left | h(x^i)\cap y^i \right |} {\left | h(x^i) \right |} \]

\[Recall(h) = \frac{1}{p}\sum_{i=1}^{p}\frac{\left | h(x^i)\cap y^i \right |} {\left | y^i \right |} \]

\[F^{\beta}(h) = \frac{(1+\beta^2) \cdot Precision(h) \cdot Recall(h)}{\beta^2 \cdot Precision(h) \cdot Recall(h)} \]

4. One-error（度量的是：“预测到的最相关的标签” 不在 “真实标签”中的样本占比。值越小，表现越好）

\[one-error(f) = \frac{1}{p}\sum_{i=1}^{p} 1\{ [arg \; \mathop {max}\limits_{y_j \in Y} \; f(x^i, y_j)] \notin y^i\} \]

5. Coverage（度量的是：“排序好的标签列表”平均需要移动多少步，才能覆盖真实的相关标签集）

\[coverage(f) = \frac{1}{p}\sum_{i=1}^{p} \mathop {max}\limits_{y_j \in y^i} \; rank_f(x^i, y_j) - 1 \]

其中$ rank_f(x^i, y_j) $ 表示用\(f(\cdot, \cdot)\) 对\(Y\)中的所有标签（注意是对\(Y\)中所有标签）进行降序排序，给个排名，最后返回的是\(y_j\)标签在这个排序列表中的一个排名，排名越大，相关性越小。而 \(\mathop {max}\limits_{y_j \in y^i}\)表示取到，真实标签\(y^i\)中的标签在上面这个排名中最大的，那个排名。
如果真实标签\(y^i\)被完全预测正确的话，取到的值是$\left | y^i \right | \(，\)y^i\(中的排名就是从1到\)\left | y^i \right | \(。 如果\)y^i\(中有一个标签\)y_j\(没有被预测正确，那么取的值就是那个标签\)y_j\(在\)Y\(中的排名，因为预测正确的那些都是排名最小（相关性最大）的那些标签，这个\)y_j\(肯定是大于\)\left | y^i \right | $的。

6. Ranking Loss（度量的是：反序标签对的占比，也就是不相关标签比相关标签的相关性还要大的情况）

\[ rloss(f) = \frac{1}{p}\sum_{i=1}^{p} \frac{1}{ \left | y^i \right | \left | \overline{y^i}\right | } \left | \{ (y_{j1}, y_{j2}) \; | \; f(x^i, y_{j1}) \leq f(x^i, y_{j2}) \; , \; (y_{j1}, y_{j2}) \in (y^i \times \overline{y^i}) \}\right | \]

其中\(\overline{y^i}\)为\(y^i\)在\(Y\)上的补集。\(y_{j1}\)从相关的标签集\(y^i\)中取，\(y_{j2}\)从不相关的标签集$ \overline{y^i}$中取，两两组合形成标签对。

7. Average Precision（度量的是：比特定标签更相关的那些标签的排名的占比）

\[avgprec(f) = \frac{1}{p}\sum_{i=1}^{p} \frac{1}{ \left | y^i \right | } \sum_{y_{j1} \in y^i}\frac{\left | \{ y_{j2} \; | \; rank_f(x^i, y_{j2}) \leq rank_f(x^i, y_{j1}) \; , \; y_{j2} \in y^i\} \right |}{rank_f(x^i, y_{j1})} \]

基于标签的评价指标

1. Macro-averaging

\[B_{macro}(h)= \frac{1}{q}\sum_{j=1}^{q}B(TP_j,\;FP_j,\; TN_j,\; FN_j) \]

2. Micro-averaging

\[B_{micro}(h)= B(\sum_{j=1}^{q}TP_j,\; \sum_{j=1}^{q}FP_j,\; \sum_{j=1}^{q}TN_j,\; \sum_{j=1}^{q}FN_j) \]

其中\(TP_j,\;FP_j,\; TN_j,\; FN_j\)为单个标签下传统二分类的四个数量特征，真正例，假正例，真负例，假负例。
$B \in { Accuracy, Precision, Recall, F^\beta } $ 表示对四个数量特征进行相关运算得到常规的二分类指标。
macro是先对单个标签下的数量特征计算得到常规指标，再对多个标签取平均。
micro是先对多个标签下的数量特征取平均，再根据数量特征计算得到常规指标。

3. AUC-macro（度量的是：“排序正确”的数据对的占比，macro是先对单个标签计算，再平均）
   （这里的“排序正确”指的是根据\(f(\cdot,\cdot)\)函数，对于相关标签的打分会大于不相关标签的打分

\[AUC_{macro} = \frac{1}{q} \sum_{j=1}^{q} \frac{\left | \{ ({x}',{x}'')\;|\; f({x}',y_j) \geq f({x}'',y_j) \; , \; ({x}',{x}'') \in Z_j \times \overline{Z_j} \}\right |}{\left | Z_j \right | \left | \overline{Z_j} \right |} \]

其中\(Z_j = \{x^i \;|\; y_j \in y^i, 1 \leq i \leq p \}\)表示的是含有\(y_j\)标签的样本数量
其中\(\overline{Z_j} = \{x^i \;|\; y_j \notin y^i, 1 \leq i \leq p \}\)表示的是不含\(y_j\)标签的样本数量。

4. AUC-micro（度量的是：“排序正确”的数据对的占比，micro是直接把多个标签考虑在内来计算占比）

\[AUC_{micro} = \frac{\left | \{ ({x}', {x}'', {y}', {y}'')\;|\; f({x}',{y}') \geq f({x}'',{y}'') \; , \; ({x}',{y}') \in S^+ \; , \; ({x}'',{y}'') \in S^- \}\right |}{\left | S^+ \right | \left | S^- \right |} \]

其中\(S^+= \{(x^i, y_j) \;|\; y_j \in y^i, 1 \leq i \leq p \}\)表示的是相关的样本标签对
其中\(S^- = \{(x^i, y_j) \;|\; y_j \notin y^i, 1 \leq i \leq p \}\)表示的是不相关的样本标签对

学习算法
可分为两类（具体算法如下图所示）

• 问题转换的方法：把多标签问题转为其它学习场景，比如转为二分类，标签排序，多分类
• 算法改编的方法：通过改编流行的学习算法去直接处理多标签数据，比如改编懒学习，决策树，核技巧。
  

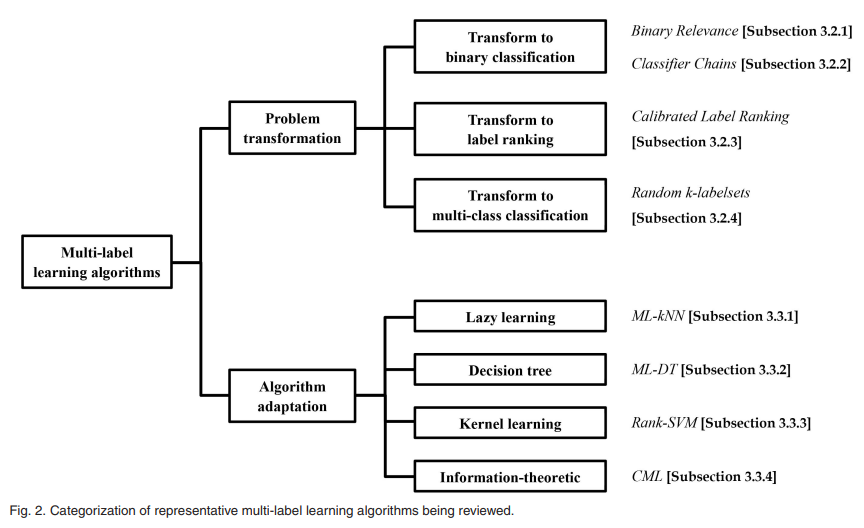
下面对图中的每个算法进行介绍。
Binary Relevance
把多个标签分离开来，对于q个标签，建立q个数据集和q个二分类器来进行预测。
这是最简单最直接的方法，是其它先进的多标签算法的基石。
没有考虑标签之间的关联性，是一个一阶策略（first-order）

Classifier Chains
首先按特定的顺序（这个顺序是自己决定的）对q个标签排个序，得到\(y_{\tau(1)}\succ y_{\tau(2)} \succ ...\succ y_{\tau(q)}\)。对于第j个标签\(y_{\tau(j)}\)构建一个二分类的数据集

\[D_{\tau(j)}=\{ ([x^i, pre^i_{\tau(j)}], 1\{ y_{\tau(j)} \in y^i \}) \; | \; 1 \leq i \leq m\} \\ where \ pre^i_{\tau(j)}=(1\{ y_{\tau(1)} \in y^i \},...,1\{ y_{\tau(j-1)} \in y^i \})^T\]

第j个标签构建的二分类数据集中，\(x^i\)会concat上前j-1个标签值。
以这样chain式的方法构建q个数据集，训练q个分类器。
在预测阶段，由于第j个分类器需要用到前j-1个分类器预测出的标签集，所以需要顺序调用这q个分类器来预测。

1. 显然算法的好坏会受到顺序\(\tau\)的影响，可以使用集成的方式，使用多个随机序列，对每个随机序列使用一部分的数据集进行训练。
2. 虽然该算法把问题分解成多个二分类，但由于它以随机的方式考虑了多个标签之间的关系，所以它是一个高阶策略（high-order）。
3. 该算法的一个缺点是丢失了平行计算的机会，因为它需要链式调用来进行预测

Calibrated Label Ranking
算法的基本思想是把多标签学习问题转为标签排序问题，该算法通过“成对比较”来实现标签间的排序。
对q个标签，可以构建q(q-1)/2个标签对，所以可以构建q(q-1)/2个数据集。

\[ D_{jk} = \{ (x_i, \psi (y^i, y_j, y_k)) \; | \; \phi (y^i, y_j) \neq \phi (y^i, y_k), 1 \leq i \leq m \} \\ where \ \psi (y^i, y_j, y_k)) = \left\{\begin{matrix} +1, & if \ \phi (y^i, y_j) = +1 \ and \ \phi (y^i, y_k) = -1\\ -1, & if \ \phi (y^i, y_j) = -1 \ and \ \phi (y^i, y_k) = +1 \end{matrix}\right. \\ \phi (y^i, y_j) = \left\{\begin{matrix} +1 & if \ y_j \in y^i\\ -1 & else \end{matrix}\right.\]

1. 只有带有不同相关性的两个标签\(y_j\)和\(y_k\)的样本才会被包含在数据集\(D_{jk}\)中，用该数据集训练一个分类器，当分类器返回大于0时，样本属于标签\(y_j\)，否则属于标签\(y_k\)。
2. 可以看到，每个样本\(x^i\)会被包含在\(\left | y^i \right | \left | \overline{y^i} \right |\)个分类器中。
3. 在预测阶段，根据分类器，每个样本和某个标签会产生一系列的投票，根据投票行为来做出最终预测。
4. 前面构造二分类器的方法使用one-vs-rest的方式，本算法使用one-vs-one，缓和类间不均衡的问题。
5. 缺点在于复杂性高，构建的分类器个数为q(q-1)/2，表现为二次增长。
6. 考虑两个标签之间的关联，是二阶策略（second-order）

Random k-Labelsets
算法的基本思想是把多标签学习问题转为多分类问题。把\(2^q\)个可能的标签集，映射成\(2^q\)个自然数。
映射函数记为\(\sigma _Y\)，则原数据集变为\(D^+_Y = \{ (x^i, \sigma_Y(y^i)) \ | \ 1 \leq i \leq m \}\)。
所对应的新类别记为 $ \Gamma(D^+_Y) = { \sigma_Y(y^i) \ | \ 1 \leq i \leq m}\(，显然\) \left | \Gamma(D^+_Y) \right | \leq min(m, 2^{|Y|})$。
这样来训练一个多分类器，最后根据输出的自然数映射回标签集的算法称为LP（Label Powerest）算法，它有两个主要的局限性

1. LP预测的标签集是训练集中已经出现的，它没法泛化到未见过的标签集
2. 类别太大，低效

为了克服LP的局限性，Random k-Labelsets使用的LP分类器只训练Y中的一个长度为k的子集，然后集成大量的LP分类器来预测。
\(Y^k\)表示\(Y\)的所有的长度为k的子集，\(Y^k(l)\)表示随机取的一个长度为k的子集，这样就可以进行收缩样本空间，得到如下样本集和标签集。

\[D^+_{Y^k(l)}= \{ (x^i, \sigma_{Y^k(l)}(y^i \cap Y^k(l) )) \ | \ 1 \leq i \leq m \} \]

\[\Gamma(D^+_{Y^k(l)})= \{ \sigma_{Y^k(l)}(y^i \cap Y^k(l) ) \ | \ 1 \leq i \leq m \} \]

更进一步，我们随机取n个这样的子集：\(Y^k(l_r), 1 \leq r \leq n\)来构造n个分类器做集成。
最后预测的时候需要计算两个指标，一个为标签j能达到的最大投票数，一个为实际投票数。

\[\tau(x, y_j) = \sum_{r=1}^{n} 1\{ y_j \in Y^k(l_r)\} \]

\[\mu (x, y_j) = \sum_{r=1}^{n} 1\{ y_j \in \sigma_{Y^k(l)}^{-1}(g^+_{Y^k(l)}(x) )\} \]

其中$ \sigma_{Y^k(l)}(\cdot)\(表示从自然数映射回标签集的函数，\)g^+(\cdot)$表示分类器学习到的函数。最后预测的时以0.5为阈值进行预测，得到标签集。

\[y = \{ y_j \ | \ \mu (x, y_j) \ / \ \tau(x, y_j) > 0.5\ , \ 1 \leq j \leq q\} \]

因为是随机长度为k的子集，考虑了多个标签之间的相关性，所以是高阶策略（high-order）。

Multi-Label k-Nearest Neighbor（ML-KNN）
用\(N(x)\)表示x的\(k\)个邻居，则\(C_j = \sum_{(x,y) \in N(x)} 1\{y_j \in y\}\)表示样本x的邻居中带有标签\(y_j\)的邻居个数。 用\(H_j\)表示样本x含有标签\(y_j\)，根据后验概率最大化的规则，有

\[y = \{y_j \ | \ P(H_j \ | \ C_j)\ / \ P(\urcorner H_j \ | \ C_j) > 1 \ , \ 1 \leq j \leq q \} \]

根据贝叶斯规则，有

\[\frac{P(H_j \ | \ C_j)} {P(\urcorner H_j\ | \ C_j)} = \frac {P(H) \cdot P(C_j \ | \ H_j)} {P(\urcorner H) \cdot P(C_j \ | \ H_j)} \]

先验概率\(P(H_j), P(\urcorner H_j)\)可以通过训练集计算得到，表示样本带有或不带有标签\(y_q\)的概率

\[P(H_j) = \frac { s + \sum_{i=1}^{m} 1\{ y_j \in y^i \} } {s \times 2 + m} \\ P(\urcorner H_j) = 1 - P(H_j) \ \ (1 \leq j \leq q)\]

其中s是平滑因子，s为1时则使用的是拉普拉斯平滑。
条件概率的计算需要用到两个值

\[\kappa_j[r] = \sum_{i=1}^{m} 1\{ y_j \in y^i \} \cdot 1\{ \delta_j(x^i) = r \} \ \ \ \ (0 \leq r \leq k) \\ \tilde{\kappa}_j[r] = \sum_{i=1}^{m} 1\{ y_j \notin y^i \} \cdot 1\{ \delta_j(x^i) = r \} \ \ \ \ (0 \leq r \leq k) \\ where \ \ \delta_j(x^i) = \sum_{(x^*,y^*) \in N(x^i)} 1 \{y_j \in y^*\}\]

\(\kappa_j[r]\)表示“含有标签\(y_j\)而且r个邻居也含有标签\(y_j\)的”样本的个数。
\(\tilde{\kappa}_j[r]\)表示“不含有标签\(y_j\)但是r个邻居含有\(y_j\)的”样本的个数。
根据这两个值，可以计算相应的条件概率

\[P(C_j \ | \ H_j) = \frac{s+\kappa_j[C_j]} {s \times (k+1) + \sum_{r=0}^{k} \kappa_j[r]} \ \ (1 \leq j \leq q, 0 \leq C_j \leq k) \\ P(C_j \ | \ \urcorner H_j) = \frac{s+\tilde{\kappa}_j[C_j]} {s \times (k+1) + \sum_{r=0}^{k} \tilde{\kappa}_j[r]} \ \ (1 \leq j \leq q, 0 \leq C_j \leq k) \]

这两个条件概率表示的是，样本带有或不带有标签\(y_j\)的条件下，它有\(C_j\)个邻居带有标签\(y_j\)的概率。

1. 由上述的条件概率，先验概率则可以根据贝叶斯规则和后验概率最大化，计算出样本的标签集
2. 需要注意的是该方法不是KNN和独立二分类的简单结合，因为算法中还使用了贝叶斯来推理邻居信息
3. 没有考虑标签之间的相关性，是一阶策略（first-order）

Multi-Label Decision Tree（ML-DT）
使用决策树的思想来处理多标签数据，数据集T中，使用第l个特征，划分值为\(\vartheta\)，计算出如下信息增益：

\[IG(T, l, \vartheta ) = MLEnt(T) - \sum_{\rho \in \{-, +\} } \frac{|T^{\rho }|} {\left | T \right |} \cdot MLEnt(T^{\rho}) \\ where \ \ T^- = \{ (x^i, y^i) \ | \ x_{il} \leq v, 1 \leq i \leq n\} \\ where \ \ T^+ = \{ (x^i, y^i) \ | \ x_{il} \gt v, 1 \leq i \leq n\} \]

递归地构建一颗决策树，每次选取特征和划分值，使得上式的信息增益最大。
其中式子中的熵的公式可以按如下计算（为了方便计算，假定标签之间独立）。

\[MLEnt(T) = \sum_{j=1}^{q} -p_j log_2p_j - (1-p_j)log_2(1-p_j) \\ where \ \ p_j= \frac {\sum_{i=1}^{n} 1\{ y_j \in y^i \}} {n}\]

1. 新样本到来时，向下遍历决策树的结点，找到叶子结点，若\(p_j\)大于0.5则表示含有标签\(y_j\)
2. 该算法不是决策树和独立二分类的简单结合（如果是的话，应该构建q棵决策树）
3. 没有考虑标签的相关性，是一阶策略（first-order）

Ranking Support Vector Machine（Rank-SVM）
使用最大间隔的思想来处理多标签数据。
Rank-SVM考虑系统对相关标签和不相关标签的排序能力。
考虑最小化\(x^i\)到每一个“相关-不相关”标签对的超平面的距离，来得到间隔。

\[\min_{(x^i, y^i) \in D} \min_{(y_j, y_k) \in y^i \times \overline{y^i}} \frac{ \langle w_j-w_k,x^i \rangle +b_j-b_k}{\left \| w_j - w_k\right \|} \]

像SVM一样对w和b进行缩放变换后可以对式子进行改写，然后最大化间隔，再调换分子分母进行改写，得到：

\[ \begin{matrix} \min_{w} & \max_{1 \leq j < k \leq q} {\left \| w_j - w_k\right \|^2}\\ subject\ to: & \; \langle w_j - w_k, x^i \rangle + b_j - b_k \geq 1 \\ & (1 \leq i \leq m, \ \ (y_i,y_k) \in y^i \times \overline{y^i}) \end{matrix}\]

为了简化，用sum操作来近似max操作

\[ \begin{matrix} \min_{w} & \sum_{j=1}^q {\left \| w_j \right \|^2}\\ subject\ to: & \; \langle w_j - w_k, x^i \rangle + b_j - b_k \geq 1 \\ & (1 \leq i \leq m, \ \ (y_i,y_k) \in y^i \times \overline{y^i}) \end{matrix} \]

跟SVM一样，为了软间隔最大化，引入松弛变量，得到下式：

\[ \begin{matrix} \min_{w, \Xi } & \sum_{j=1}^q {\left \| w_j \right \|^2} + C \sum_{i=1}^m \frac {1}{\left | y^i \right | \left | \overline{y^i} \right | } \sum_{(y_i,y_k) \in y^i \times \overline{y^i})} \xi _{ijk} \\ subject\ to: & \; \langle w_j - w_k, x^i \rangle + b_j - b_k \geq 1 - \xi _{ijk}\\ & \xi _{ijk} > 0 \ (1 \leq i \leq m, \ \ (y_i,y_k) \in y^i \times \overline{y^i}) \end{matrix} \\\]

其中\(\Xi = \{ \xi_{ijk} \ | \ 1 \leq i \leq m, \ (y_i,y_k) \in y^i \times \overline{y^i} \}\)

1. 跟SVM一样，最终的式子是一个二次规划问题，通常调用现有的包来解。
2. 对于非线性问题则使用核技巧来解决。
3. 由于定义了”相关-不相关“标签对的超平面，这是个二阶策略（second-order）

Collective Multi-Label Classifier（CML）
该算法的核心思想最大熵原则。用\((x,y),\)表示任意的一个多标签样本，其中\(y = (y_1, y_2, ..., y_q) \in \{-1, +1\}^q\)。
算法的任务等价于学习一个联合概率分布\(p(x,y)\)，用\(H_p(x,y)\)表示给定概率分布\(p\)时\((x,y)\)的信息熵。
最大熵原则认为熵最大的模型是最好的模型。

\[ \begin{matrix} &\max_{p} H_p(x,y) \\ &subject \ to: E_p[f_k(x,y)] = F_k \ (k \in K) \end{matrix} \]

其中\(f_k(x,y)\)是一个特征函数，描述\(x\)和\(y\)之间的一个事实\(k\)，满足这个事实时返回1，否则返回0。
约束做的是希望这个分布上，特征函数的期望能够等于一个我们希望的值\(F_k\)，这个值通常通过训练集来估计。
解这个优化问题，会得到

\[p(y|x) = \frac{1}{Z_{\Lambda}(x) } exp(\sum_{k \in K} \lambda_k \cdot f_k(x,y)) \]

其中\(\Lambda = \{ \lambda_k | k \in K \}\)表示一系列的权重。$Z_{\Lambda} = \sum_y exp(\sum_{k \in K} \lambda_k \cdot f_k(x,y)) \(作为规范化因子。 假设有一个高斯先验\)\lambda_k \sim N(0, \varepsilon^2)\(，就可以通过最大化以下这个log后验概率来求得参数\)\Lambda$。

\[ \begin{matrix} l(\Lambda | D) & = log P(D|\Lambda) + log P(\Lambda) \\ & = log \prod_{(x,y) \in D} p(y|x) + log P(\Lambda) \\ & = log(\prod_{(x,y) \in D} p(y|x)) - \sum_{k \in K} \frac {\lambda^2}{2 \varepsilon^2} \\ \end{matrix}\]

1. 这是个凸函数，可以调用现成的无约束优化方法比如BFGS直接求解。求得参数就可以得到要学习的概率分布\(p(y|x)\)。
2. 对于一系列约束K，分为两个部分
3. \(K_1 = \{ (l,j) | 1 \leq l \leq d, 1 \leq j \leq q\}\)，有\(d \cdot q\)个约束，特征函数为

\[f_k(x,y) = x_l \cdot 1 \{ y_j == 1 \} , \ \ k = (l,j) \in K_1 \]

4. $K_2 = { (j_1, j_2, b_1, b_2) | 1 \leq j_1 < j_2 \leq q, \ \ b_1, b_2 \in { -1, +1 } } $，有\(4 \cdot \binom{q}{2}\)个约束，特征函数为

\[f_k(x,y) = 1 \{ y_{j1} = b_1 \} \cdot 1 \{ y_{j2} = b_2 \}, \ \ k = (j_1, j_2, b_1, b_2) \in K_2 \]

5. 由于K约束中考虑了标签对之间的关联，该算法是个二阶策略（second-order）。

相关任务

1. 多实例学习（Multi-instance learning）：每个样本由多个实例和一个标签组成，多个实例中至少一个为正，认为该样本为正。和多标签学习的输出空间模糊相反，多实例学习是输入空间模糊。
2. 有序分类（Ordinal classification）：对于每个标签，不再是简单地判断是还是否，而是改成一系列的等级排序，把\(y_j = \{-1,+1\}\)替换成\(y_j = \{m_1, m_2, ..., m_k\}, \ where \ m_1 < m_2 < ... < m_k\)
3. 多任务学习（Multi-task learning）：同时训练多个任务，相关任务之间的训练信息会帮助其它任务。比如目标定位既要识别有没有目标（分类问题）又要定位出目标的位置（回归问题）。
4. 数据流学习（Data streams classification）：真实世界的目标是在线生成和实时产生的，如何处理这些数据就是数据流学习要做的事。一个关键的挑战就是“概念漂移”（目标变量的统计特性随着时间的推移以不可预见的方式变化），一般处理方式有：当一大批新数据到来时更新分类器；维持一个检测器来警惕概念漂移；假定过去数据的影响会随着时间而衰减。

总结

1. 论文主要介绍了多标签学习的一些概念定义，策略，评价指标，以及8个有代表性的算法，其中对多种评价指标和多个算法都做了清晰的分类和详细的阐述。
2. 尽管挖掘标签关联性的想法被应用到许多算法中，但是仍然没有一个正式的机制。有研究表示多标签之间的关联可能是非对称的（我对你的影响和你对我的影响是不同的），局部的（不同样本之间的标签相关性不同，很少关联性是所有样本都满足的）。
3. 但是不管怎么说，充分理解和挖掘标签之间的相关性，是多标签学习的法宝。尤其是巨大输出空间场景下。