论文笔记:空间变换网络(Spatial Transformer Networks)
2015, NIPS
**Max Jaderberg, Karen Simonyan, Andrew Zisserman, Koray Kavukcuoglu **
Google DeepMind
为什么提出(Why)
- 一个理想中的模型:我们希望鲁棒的图像处理模型具有空间不变性,当目标发生某种转化后,模型依然能给出同样的正确的结果
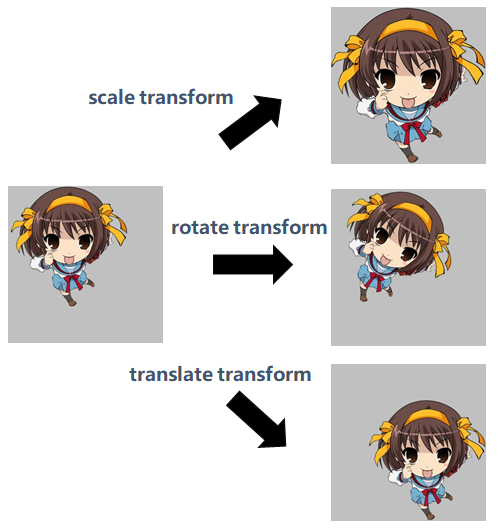
- 什么是空间不变性:举例来说,如下图所示,假设一个模型能准确把左图中的人物分类为凉宫春日,当这个目标做了放大、旋转、平移后,模型仍然能够正确分类,我们就说这个模型在这个任务上具有尺度不变性,旋转不变性,平移不变性
- CNN在这方面的能力是不足的:maxpooling的机制给了CNN一点点这样的能力,当目标在池化单元内任意变换的话,激活的值可能是相同的,这就带来了一点点的不变性。但是池化单元一般都很小(一般是2*2),只有在深层的时候特征被处理成很小的feature map的时候这种情况才会发生
- Spatial Transformer:本文提出的空间变换网络STN(Spatial Transformer Networks)可以使得模型具有空间不变性。
STN是什么(What)
- STN对feature map(包括输入图像)进行空间变换,输出一张新的图像。
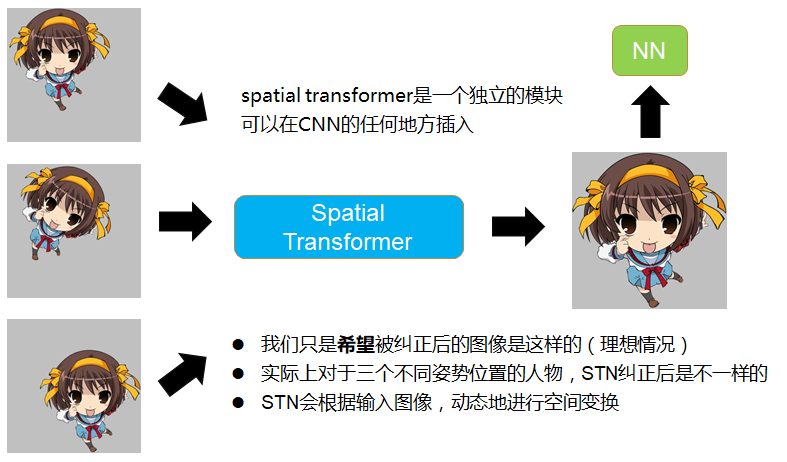
- 我们希望STN对feature map进行变换后能把图像纠正到成理想的图像,然后丢进NN去识别,举例来说,如下图所示,输入模型的图像可能是摆着各种姿势,摆在不同位置的凉宫春日,我们希望STN把它纠正到图像的正中央,放大,占满整个屏幕,然后再丢进CNN去识别。
- 这个网络可以作为单独的模块,可以在CNN的任何地方插入,所以STN的输入不止是输入图像,可以是CNN中间层的feature map
STN是怎么做的(How)
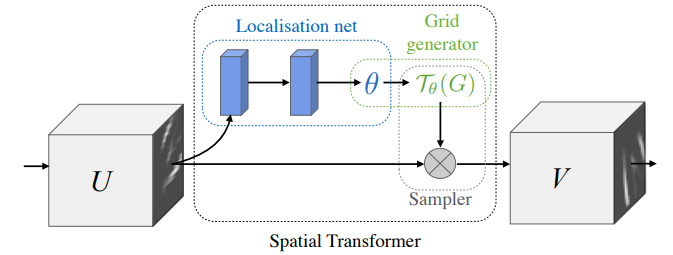
- 如下图所示,STN的输入为U,输出为V,因为输入可能是中间层的feature map,所以画成了立方体(多channel),STN主要分为下述三个步骤
- Localisation net:是一个自己定义的网络,它输入U,输出变化参数\(\Theta\),这个参数用来映射U和V的坐标关系
- Grid generator:根据V中的坐标点和变化参数\(\Theta\),计算出U中的坐标点。这里是因为V的大小是自己先定义好的,当然可以得到V的所有坐标点,而填充V中每个坐标点的像素值的时候,要从U中去取,所以根据V中每个坐标点和变化参数\(\Theta\)进行运算,得到一个坐标。在sampler中就是根据这个坐标去U中找到像素值,这样子来填充V
- Sampler:要做的是填充V,根据Grid generator得到的一系列坐标和原图U(因为像素值要从U中取)来填充,因为计算出来的坐标可能为小数,要用另外的方法来填充,比如双线性插值。
下面针对每个模块阐述一下
(1) Localisation net
这个模块就是输入U,输出一个变化参数\(\Theta\),那么这个\(\Theta\)具体是指什么呢?
我们知道线性代数里,图像的平移,旋转和缩放都可以用矩阵运算来做
举例来说,如果想放大图像中的目标,可以这么运算,把(x,y)中的像素值填充到(x',y')上去,比如把原来(2,2)上的像素点,填充到(4,4)上去。
\(\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}2 &0\\0&2\end{bmatrix}\begin{bmatrix}x\\y\end{bmatrix}+\begin{bmatrix}0\\ 0\end{bmatrix}\)
如果想旋转图像中的目标,可以这么运算(可以在极坐标系中推出来,证明放到最后的附录)
\(\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}cos \Theta & -sin \Theta\\ sin \Theta& cos\Theta\end{bmatrix} \begin{bmatrix}x\\ y\end{bmatrix}+\begin{bmatrix}0\\ 0\end{bmatrix}\)
这些都是属于仿射变换(affine transformation)
\(\begin{bmatrix}x^{'}\\ y^{'}\end{bmatrix}=\begin{bmatrix}a & b \\ c& d\end{bmatrix} \begin{bmatrix}x\\ y\end{bmatrix}+\begin{bmatrix}e\\ f\end{bmatrix}\)
在仿射变化中,变化参数就是这6个变量,\(\Theta = \{a,b,c,d,e,f\}\)(此\(\Theta\)跟上述旋转变化里的角度\(\Theta\)无关)
这6个变量就是用来映射输入图和输出图之间的坐标点的关系的,我们在第二步grid generator就要根据这个变化参数,来获取原图的坐标点。
(2) Grid generator
有了第一步的变化参数,这一步是做个矩阵运算,这个运算是以目标图V的所有坐标点为自变量,以$ \Theta $为参数做一个矩阵运算,得到输入图U的坐标点。
其中$ {(x_{i}{t},y_{i})}\(记为输出图V中的第i个坐标点,V中的长宽可以和U不一样,自己定义的,所以这里用i来标识第几个坐标点 \) {(x_{i}{s},y_{i})}$记为输入图U中的点,这里的i是从V中对应过来的,表示V中的第i的坐标点映射的U中坐标,i跟U没有关系
(3) Sampler
由于在第二步计算出了V中每个点对应到U的坐标点,在这一步就可以直接根据V的坐标点取得对应到U中坐标点的像素值来进行填充,而不需要经过矩阵运算。需要注意的是,填充并不是直接填充,首先计算出来的坐标可能是小数,要处理一下,其次填充的时候往往要考虑周围的其它像素值。填充根据的公式如下。
其中n和m会遍历原图U的所有坐标点,\(U_{nm}\)指原图U中某个点的像素值,k()为取样核,两个\(\phi\)为参数,\((x_{i}^{s},y_{i}^{s})\)表示V中第i个点要到U图中找的对应点的坐标,表示的坐标是U图上的,k表示使用不同的方法来填充,通常会使用双线性插值,则会得到下面的公式
举例来说,我要填充目标图V中的(2,2)这个点的像素值,经过以下计算得到(1.6,2.4)
如果四舍五入后直接填充,则难以做梯度下降。
我们知道做梯度下降时,梯度的表现就是权重发生一点点变化的时候,输出的变化会如何。
如果用四舍五入后直接填充,那么(1.6,2.4)四舍五入后变成(2,2)
当\(\Theta\)(我们求导的时候是需要对\(\Theta\)求导的)有一点点变化的时候,(1.6,2.4)可能变成了(1.9,2.1)四舍五入后还是变成(2,2),输出并没有变化,对\(\Theta\)的梯度没有改变,这个时候没法用梯度下降来优化\(\Theta\)
如果采用上面双线性插值的公式来填充,在这个例子里就会考虑(2,2)周围的四个点来填充,这样子,当\(\Theta\)有一点点变化的时,式子的输出就会有变化,因为$(x_{i}{s},y_{i}) $的变化会引起V的变化。注意下式中U的下标,第一个下标是纵坐标,第二个下标才是横坐标。
(4) STN小结
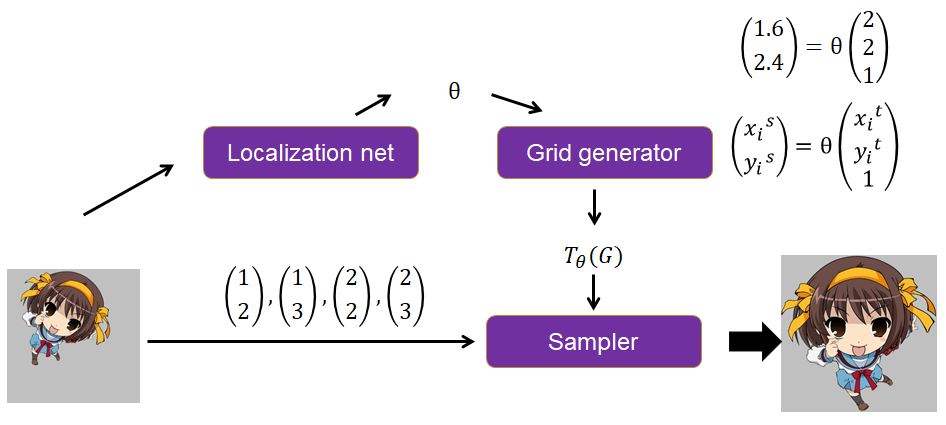
简单总结一下,如下图所示
- Localization net根据输入图,计算得到一个\(\Theta\)
- Grid generator根据输出图的坐标点和\(\Theta\),计算出输入图的坐标点,举例来说想知道输出图上(2,2)应该填充什么坐标点,则跟\(\Theta\)运算,得到(1.6,2.4)
- Sampler根据自己定义的填充规则(一般用双线性插值)来填充,比如(2,2)坐标对应到输入图上的坐标为(1.6,2.4),那么就要根据输入图上(1.6,2.4)周围的四个坐标点(1,2),(1,3),(2,2),(2,3)的像素值来填充。
【实验】Distorted MNIST

【实验】SVHN: Street View House Numbers

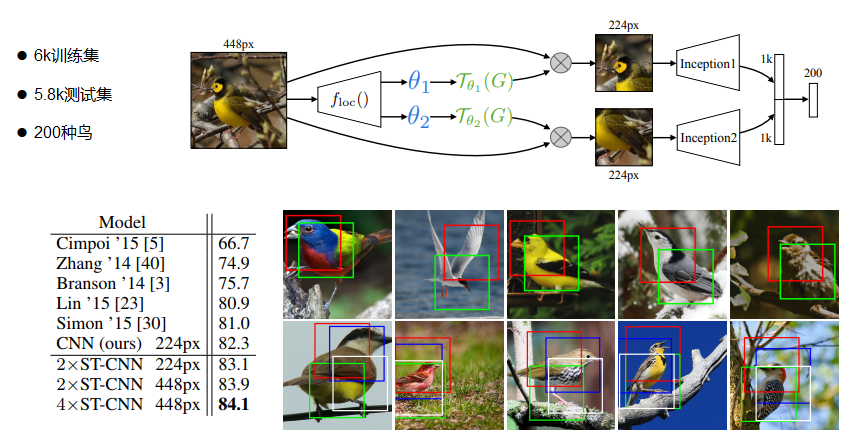
【 实验】CUB-200-2011 birds dataset
【附录】旋转的矩阵运算
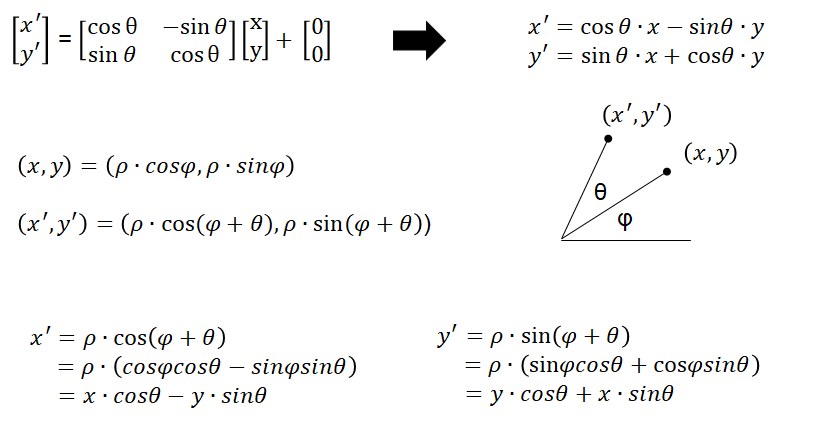



 浙公网安备 33010602011771号
浙公网安备 33010602011771号