拉格朗日对偶性

0 前言

本文承接上一篇博文拉格朗日乘子法和KKT条件http://www.cnblogs.com/liaohuiqiang/p/7805954.html，讲讲拉格朗日对偶性的问题。

在约束优化问题中，常常用拉格朗日对偶性来将原始问题转为对偶问题，通过解对偶问题的解来得到原始问题的解。

 

1 为什么要利用对偶？

首先要明确，对偶问题的解不一定直接等于原问题的解（弱对偶），但是，对偶问题有两点性质。

1.1 满足某些条件时，对偶问题直接等于原问题的解（强对偶）

1.2 无论原始问题是否是凸的，对偶问题都是凸优化问题

显然，在某些情况下，直接对对偶问题求解可以得到原问题的解，而且对偶问题是凸优化，易于求解。所以利用对偶来求解是很有用的。

 

1 原始问题

考虑原始的优化问题如下

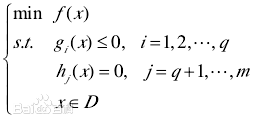
先定义拉格朗日函数$ L(x, \alpha , \beta ) = f(x) + \sum _{i=1}^q \alpha_i g_i(x) + \sum _{j=q+1}^m \beta_j h_j(x) $

考虑函数$$\Theta_P(x) = \max_{\alpha, \beta: \alpha_i\geqslant 0}L(x, \alpha , \beta ) $$

显然满足约束时函数等于f(x)，不满足约束时函数等于正无穷，容易得到$ \Theta_P(x) = \begin{Bmatrix}f(x), x\ satisfy\ constraints\\ {+ \infty, others }\end{Bmatrix} $

极小化该函数得到的$$\min_x  \Theta_P(x) =\min_x \max_{\alpha, \beta: \alpha_i\geqslant 0}L(x, \alpha , \beta ) $$和原始的优化问题是等价。

同时，我们定义原始问题的最优值为$$ p^*=\min_x  \Theta_P(x) $$

 

2 对偶问题

考虑函数$$\Theta_D(\alpha , \beta) = \min_x L(x, \alpha , \beta ) $$

极大化该函数得到$$\max_{\alpha, \beta: \alpha_i\geqslant 0} \Theta_D(\alpha ,\beta) =\max_{\alpha, \beta:\alpha_i\geqslant 0}\min_x L(x, \alpha , \beta ) $$我们把这个极大化问题视为对偶问题。

同时，我们定义对偶问题的最优值为$$ d^*=\max_{\alpha, \beta: \alpha_i\geqslant 0} \Theta_D(\alpha ,\beta) $$

 

3 原始问题和对偶问题的关系

可以得知$ d^*\leqslant p^* $，因为p是先求最大的一块区域然后在这块区域求最小，d是先求最小的一块区域然后在这块区域求最大，最大里面的最小，总会比最小里面的最大要大（或等于）。

$ d^*\leqslant p^* $，称为弱对偶，对于所有优化问题都成立，这个时候我们可以得到原始问题的一个下界。

如果$  d^*= p^* $，称为强对偶，满足某些条件才成立，这时可以用解对偶问题替代原始问题。那么满足什么样的条件可以得到强对偶呢？

如果原问题是一个凸优化，并且不等式约束g(x)是严格可行的，即存在x对所有i有$ g_i(x)<0 $，那么强对偶成立。这里需要注意的是，这里的条件只是强对偶成立的一种情况，对于非凸的问题也有可能是强对偶。

强对偶成立时，将拉格朗日函数分别对原变量x和对偶变量α和β分别求导，令导数等于零（还需要满足KKT条件），即可求解对偶问题的解，也就求得了原问题的解。

 

4 对偶求解和拉格朗日乘子法求解

对于拉格朗日乘子法求解，当原问题是凸优化的时候，考虑满足KKT的条件，对于拉格朗日函数求导等于0即可得到解。

对于对偶问题求解，转换为对偶函数求解，为了得到原始问题的解，要求强对偶，而在强对偶（不一定满足原问题凸优化）的情况下，考虑满足KKT的条件，对于拉格朗日函数求导等于0即可得到解。

当原问题是凸优化的时候，强对偶和KKT条件是互为充要条件的。