李航-统计学习方法-笔记-12：总结

10种统计学习方法特点的概括总结

本书共介绍了10种主要的统计学习方法：感知机，KNN，朴素贝叶斯，决策树，逻辑斯谛回归与最大熵模型，SVM，提升方法，EM算法，隐马尔可夫模型，条件随机场（CRF）。

适用问题

感知机，KNN，朴素贝叶斯，决策树，逻辑斯谛回归与最大熵模型，SVM，提升方法是分类方法。

原始的感知机，SVM以及提升方法是针对二分类的，可以将它们扩展到多类。

感知机，KNN，朴素贝叶斯，决策树是简单的分类方法，具有模型直观，方法简单，实现容易等特点。

逻辑斯底回归与最大熵模型，SVM和boosting是更复杂但更有效的分类方法，往往分类准确率更高。

EM算法是含有隐变量的概率模型的一般学习算法，可用于生成模型的非监督学习。

隐马和CRF是主要的标注方法。通常CRF标注准确率更高。

模型

朴素贝叶斯和隐马是概率模型。感知机，KNN，SVM，boosting是非概率模型。决策树，逻辑斯谛回归与最大熵模型，条件随机场既可以看作概率模型，也可以看作非概率模型。

朴素贝叶斯和隐马是生成模型。其它算法（除了EM算法）是判别模型。EM算法是一般方法，不具有具体模型（不属于生成模型也不属于判别模型）。

感知机是线性模型。逻辑斯谛回归，最大熵模型，CRF是对数线性模型。KNN，决策树，SVM，boosting使用的是非线性模型。

学习策略

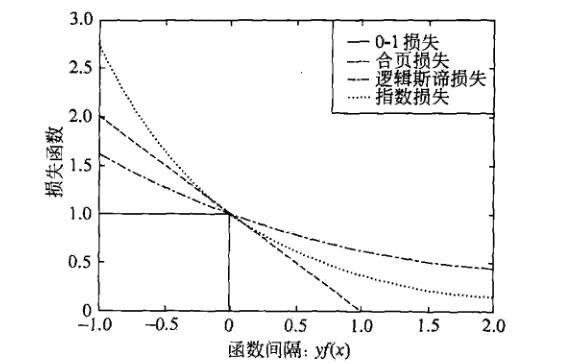
二分类学习中，SVM，逻辑斯谛回归与最大熵模型，提升方法各自使用合页损失，逻辑斯谛损失函数，指数损失函数。

\[[1-yf(x)]_+ \]

\[\log [1+exp(-yf(x))] \]

\[exp(-yf(x)) \]

这3种损失都是0-1损失的上界，具有相似的形状。可认为三种模型使用不同的代理损失表示分类损失。

定义如下结构风险

\[\min_{f \in H} \frac{1}{N} \sum_{i=1}^N L(y_i, f(x_i)) + \lambda J(f) \]

SVM用\(L_2\)范数表示模型复杂度。
原始的逻辑斯谛回归与最大熵模型没有正则化项，可以给它们加上\(L_2\)范数。
提升方法没有显式的正则化项，通过通过早停止（early stopping）的方法达到正则化的效果。

概率模型的学习可以形式化为极大似然估计或贝叶斯估计的极大后验概率估计。这时，学习的策略是极小化（正则化的）对数似然损失。对数似然损失可以写成

\[- \log P(y \ | \ x) \]

学习算法

统计学习的问题有了具体形式后，就成了最优化问题。有时，最优化问题比较简单，解析解存在，最优解可以由公式简单计算。但多数情况下，最优化问题没有解析解，需要数值计算或启发式的方法求解。

朴素贝叶斯和隐马的监督学习，最优解即极大似然估计值，可由概率计算公式直接计算。

感知机，逻辑斯谛回归与最大熵模型，CRF的学习用梯度下降法，拟牛顿法，这些都是一般的无约束优化问题的解法。

SVM学习，可解凸二次规划的对偶问题，有SMO等方法。

决策树是基于启发式算法的典型例子。可以认为特征选择，生成，剪枝是启发式进行正则化的极大似然估计。

boosting利用学习的模型是加法模型，损失函数是指数函数的特点，启发式地从前向后逐步学习模型，以达到逼近优化目标函数的目的。

EM算法是一种迭代的求解含因变量概率模型参数的方法，它的收敛性可以保证，但不能保证收敛到全局最优。

SVM，逻辑斯谛回归与最大熵模型，CRF是凸优化问题，全局最优解保证存在。而其它学习问题则不是凸优化问题。

启发式：解决问题时基于直觉或经验构造的算法。它是相对于最优化算法提出的。

复杂的最优化问题往往存在很大的问题空间，要话费大量时间精力才能求得答案。

启发式方法则是在有限的搜索空间内，大大减少尝试的数量，在可接受花费下给出问题的可行解，可行解与最优解的偏离程度一般不能被预计。