李航-统计学习方法-笔记-6：逻辑斯谛回归与最大熵模型

逻辑斯谛回归（logistic regression）是统计学习中的经典分类方法。最大熵模型是概率模型学习的一个准则，将其推广到分类问题得到最大熵模型（maximum entropy model）。逻辑斯谛回归模型与最大熵模型都属于对数线性模型。

逻辑斯谛回归

逻辑斯谛分布 ：设\(X\)是连续随机变量，\(X\)服从逻辑斯谛分布，则具有以下分布函数和密度函数。其中\(\mu\)为位置参数，\(\gamma>0\)为形状参数。

\[F(x) = P( X \leqslant x) = \frac{1}{1 + e^{-(x-\mu)/\gamma}} \]

\[f(x) = F'(x)= \frac{e^{-(x-\mu)/\gamma}}{\gamma (1 + e^{-(x-\mu)/\gamma})^2} \]

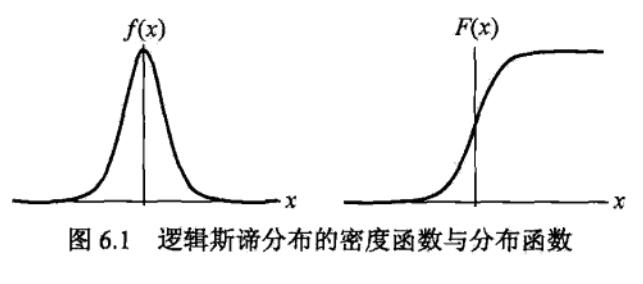
\(F(x)\)属于logistic函数，其图形是一条S形曲线，该曲线以点\((\mu, \frac{1}{2})\)为中心对称。

\[F(\mu+x) + F(\mu-x) = 2 \times \frac{1}{2} \]

曲线在中心附近增长速度较快，在两端增长速度较慢。形状参数\(\gamma\)的值越小，曲线在中心附近增长越快。

\(\mu=0, \gamma=1\)时，\(F(x)\)变成sigmoid函数。

二项逻辑斯谛回归模型（binomial logistic regression model）
是一种分类模型，由条件概率分布\(P(Y | X)\)表示，形式化为参数化的logistic分布。这里，随机变量\(X\)取值为实数，随机变量\(Y\)取值为1或0。

\[P(Y=1 \ | \ x) = \frac{exp(w \cdot x)}{1 + exp(w \cdot x)} \]

\[P(Y=0 \ | \ x) = \frac{1}{1 + exp(w \cdot x)} \]

logistic回归比较两个条件概率值的大小，将实例\(x\)分到概率值较大的那一类。

考虑logistic回归模型的特点。一个事件的几率（odds）是指该事件发生的概率与该事件不发生的概率的比值。若事件发生概率为\(p\)，则该事件的几率是\(\frac{p}{1-p}\)，对数几率是\(\log \frac{p}{1-p}\)，对logistic回归而言：

\[\log \frac{P(Y=1 \ | \ x)}{1 - P(Y=1 \ | \ x)} = w \cdot x \]

输出\(Y=1\)的对数几率是由输入\(x\)的线性函数表示的模型。

考虑对输入\(x\)进行分类的线性函数\(w \cdot x\)，通过logistic回归模型可将其转为概率。

\[P(Y=1 \ | \ x) = \frac{exp(w \cdot x)}{1 + exp(w \cdot x)} \]

这时，线性函数的值接近正无穷，概率值越接近1，线性函数的值越接近负无穷，概率值越接近0（如图6.1）。这样的模型就是logistic回归模型。

模型参数估计
学习logistic回归模型时，可以应用极大似然估计法估计模型参数。
设\(P(Y = 1 \ | \ x) = \pi(x), P(Y = 0 \ | \ x) = 1 - \pi(x)\)。

似然函数为$$\prod_{i=1}^{N} [\pi(x_i)]^{y_i} [1 - \pi(x_i)]^{1 - y_i}$$

对数似然函数为$$\begin{split} L(w) &= \sum_{i=1}^{N} [y_i \log \pi(x_i) + (1 - y_i) \log(1 - \pi(x_i))] \ &= \sum_{i=1}^{N} [y_i \log \frac{ \pi(x_i)}{(1 - \pi(x_i))} + \log(1 - \pi(x_i)) ] \ &= \sum_{i=1}^{N} [y_i (w \cdot x_i) - \log(1 + exp(w \cdot x_i)) ]\end{split}$$

（将上式第一行取反，即为交叉熵损失函数）

对\(L(w)\)求极大，得到\(w\)的估计值\(\hat{w}\)。问题变成以对数似然函数为目标的最优化问题，logistic回归学习中通常采用梯度下降法及拟牛顿法。

多项逻辑斯谛回归（multi-nominal logistic regression model）
推广到多分类，假设离散型随机变量\(Y\)的取值集合是\(\{1, 2, ..., K\}\)，那么多项logistic回归模型是

\[P(Y = k \ | \ x) = \frac{exp(w_k \cdot x)}{1 + \sum_{k=1}^{K-1}exp(w_k \cdot x)}, k = 1, 2, ..., K-1 \]

\[P(Y = K \ | \ x) = \frac{1}{1 + \sum_{k=1}^{K-1}exp(w_k \cdot x)} \]

最大熵模型

最大熵原理
最大熵原理是概率模型学习的一个准则，认为在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。

通常用约束条件来确定概率模型的集合，所以最大熵原理可表述为“在满足约束条件的模型集合中选取熵最大的模型”。

\[H(P) = - \sum_{x} P(x) \log P(x), \\ 0 \leqslant H(P) \leqslant \log |X| \]

\(|X|\)是\(X\)的取值个数，当且仅当\(X\)是均匀分布时，不等式右边的等号成立，熵最大。

最大熵原理认为要选择的概率模型首先必须满足已有的事实，即约束条件。在没有更多信息的情况下，那些不确定的部分是“等可能的”，等概率表示了对事实的无知。因为没有更多信息，这种判断是合理的，“等可能”不易操作，可通过“熵最大”来表示。

最大熵模型
最大熵原理是统计学习的一般原理，将它应用到分类得到最大熵模型。

给定训练数据，可以确定联合分布\(P(X, Y)\)的经验分布和边缘分布\(P(X)\)的经验分布，分别以\(\tilde{P}(X, Y)\)和\(\tilde{P}(X)\)表示

\[\tilde{P}(X = x, Y = y) = \frac{v(X=x, Y=y)}{N} \]

\[\tilde{P}(X = x) = \frac{v(X=x)}{N} \]

其中\(v(X=x, Y=y)\)表示训练数据中样本\((x, y)\)出现的频数，\(v(X=x)\)表示训练数据中输入\(x\)出现的频数，\(N\)表示训练样本容量。

用特征函数\(f(x, y)\)描述\(x\)和\(y\)之间的某一事实，它是一个二值函数（一般地，特征函数可以是任意实值函数）。

\[f(x, y) = \left\{\begin{matrix} 1, & x与y满足某一事实\\ 0, & 否则 \end{matrix}\right.\]

特征函数\(f(x, y)\)关于经验分布\(\tilde{P}(X, Y)\)的期望值，用\(E_{\tilde{P}}(f)\)表示。

\[E_{\tilde{P}}(f) = \sum_{x, y} \tilde{P}(x, y) \ f(x, y) \]

特征函数\(f(x, y)\)关于模型\(P(Y \ | \ X)\)与经验分布\(\tilde{P}(X)\)的期望值，用\(E_{P}(f)\)表示。

\[E_P(f) = \sum_{x, y} \tilde{P}(x) \ P(y \ | \ x) \ f(x, y) \]

如果模型能够获取训练数据中的信息，那么就可以假设这里两个期望值相等，即

\(E_P(f) = E_{\tilde{P}}(f), \tag{6.10}\)
或

\[\sum_{x, y} \tilde{P}(x) \ P(y \ | \ x) \ f(x, y) = \sum_{x, y} \tilde{P}(x, y) \ f(x, y), \tag{6.11} \]

将式(6.10)或式(6.11)作为模型学习的约束条件，假如有\(n\)个特征函数\(f_i(x, y), i=1, 2, ..., n\)，那么就有n个约束条件。

最大熵模型的定义
假设满足所有约束条件的模型集合为：

\[\mathcal{C} \equiv \{P \in \mathcal{P} \ | \ E_P(f_i) = E_{\tilde{P}}(f_i), i = 1, 2, ..., n\} \]

定义在条件概率分布\(P( Y \ | \ X)\)上的条件熵为：

\[H(P) = - \sum_{x, y} \tilde{P}(x) \ P( y \ | \ x) \log P(y \ | \ x) \]

则模型集合\(\mathcal{C}\)中条件熵\(H(P)\)最大的模型称为最大熵模型。式中的对数为自然对数。

最大熵模型的学习

最大熵模型的学习等价于以下约束最优化问题：

\[\max_{P \in \mathcal{C}} H(P) = - \sum_{x, y} \tilde{P}(x) \ P( y \ | \ x) \log P(y \ | \ x) \]

\[\begin{split} s.t. \ \ & E_P(f_i) = E_{\tilde{P}} (f_i), \ \ i = 1, 2, ..., n \\ & \sum_y P( y \ | \ x) = 1\end{split}\]

按照最优化问题的习惯，将求最大值问题改写为等价的求最小值问题：

\[\min_{P \in \mathcal{C}} - H(P) = \sum_{x, y} \tilde{P}(x) \ P( y \ | \ x) \log P(y \ | \ x) \]

\[\begin{split} s.t. \ \ & E_P(f_i) - E_{\tilde{P}} (f_i) = 0, \ \ i = 1, 2, ..., n \\ & \sum_y P( y \ | \ x) = 1\end{split}\]

定义拉格朗日函数\(L(P, w)\)：

\[\begin{split} L(P, w) = &- H(P) + w_0 (1 - \sum_y P( y \ | \ x)) +\\ & \sum_{i=1}^{n} w_i (E_P(f_i) - E_{\tilde{P}} (f_i)) \end{split} \tag{6.17}\]

最优化的原始问题为：

\[\min_{P \in \mathcal{C}} \max_{w} L(P, w), \tag{6.18} \]

对偶问题是：

\[\max_{w} \min_{P \in \mathcal{C}} L(P, w), \tag{6.19} \]

由于拉格朗日函数\(L(P, w)\)是\(P\)的凸函数，原始问题(6.18)的解与对偶问题(6.19)的解是等价的。这样，可以通过求解对偶问题(6.19)来求解原始问题(6.18)。

首先求解对偶问题(6.19)内部的极小化问题\(\min_{P \in \mathcal{C}} L(P, w)\)，得到的函数是\(w\)的函数，将其记作：

\[\Psi(w) = \min_{P \in \mathcal{C}} L(P, w) = L(P_w, w), \tag{6.20} \]

\(\Psi(w)\)称为对偶函数，同时，将其解记作

\[P_w = \arg \min_{P \in \mathcal{C}} L(P, w) = P_w( y \ | \ x) \]

具体地，求\(L(P, w)\)对\(P( y \ | \ x)\)的偏导数，另偏导数等于0，解得

\[P( y \ | \ x) = exp(\sum_{i=1}^{n} w_i \ f_i(x, y) + w_0 - 1) = \frac{exp(\sum_{i=1}^{n} w_i \ f_i(x, y))}{exp( w_0 - 1)} \]

由于$ \sum_y P( y \ | \ x) = 1$，得

\[P_w( y \ | \ x) = \frac{exp(\sum_{i=1}^{n} w_i \ f_i(x, y))}{Z_w(x)}, \tag{6.22} \]

\[Z_w(x) = \sum_y exp(\sum_{i=1}^{n} w_i \ f_i(x, y)), \tag{6.23} \]

之后求解对偶问题(6.19)外部的极大化问题\(\max_w \Psi(w)\)，将其解记为\(w^*\)，即\(w^* = \arg \max_w \Psi(w)\)，可以应用最优化算法求解得到\(w^*\)，代入\(P_w( y \ | \ x)\)得到\(P_{w^*}( y \ | \ x)\)，即学习到的最优模型（最大熵模型）。

极大似然估计

从以上最大熵模型学习中可以看出，最大熵模型是由式(6.22)、式(6.23)表示的条件概率分布。下面证明对偶函数的极大化等价于最大熵模型的极大似然估计。

已知训练数据的经验概率分布\(\tilde{P}(X, Y)\)，条件概率分布\(P(Y \ | \ X)\)的对数似然函数表示为

\[L_{\tilde{P}}(P_w) = \log \prod_{x, y} P( y \ | \ x)^{\tilde{P}(x, y)} = \sum_{x, y} \tilde{P}(x, y) \log P( y \ | \ x) \]

当条件概率分布$ P( y \ | \ x)\(是最大熵模型(6.22)和(6.23)时，对数似然函数\)L_{\tilde{P}}(P_w)$为：

\[\begin{split}L_{\tilde{P}}(P_w) &= \sum_{x, y} \tilde{P}(x, y) \log P( y \ | \ x) \\ &= \sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n} w_i \ f_i(x, y) - \sum_{x, y} \tilde{P}(x, y) \log Z_w(x) \\ &= \sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n} w_i \ f_i(x, y) - \sum_{x} \tilde{P}(x) \log Z_w(x)\end{split} \]

再看对偶函数\(\Psi(w)\)，由式(6.17)及式(6.20)可得

\[\begin{split} \Psi(w) =& \sum_{x, y} \tilde{P}(x) \ P_w( y \ | \ x) \log P_w(y \ | \ x) \\ &+ \sum_{i=1}^{n} w_i (\sum_{x, y} \tilde{P}(x, y) \ f_i(x, y) - \sum_{x, y} \tilde{P}(x) \ P_w( y \ | \ x) \ f_i(x, y)) \\ =& \sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n} w_i \ f_i(x, y) + \sum_{x, y} \tilde{P}(x) \ P_w( y \ | \ x) (\log P_w(y \ | \ x) - \sum_{i=1}^{n} w_i f_i(x, y)) \\ =& \sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n} w_i \ f_i(x, y) - \sum_{x, y} \tilde{P}(x) \ P_w( y \ | \ x) \log Z_w(x) \\ =& \sum_{x, y} \tilde{P}(x, y) \sum_{i=1}^{n} w_i \ f_i(x, y) - \sum_{x} \tilde{P}(x) \log Z_w(x) \\ \end{split}\]

可以发现\(L_{\tilde{P}}(P_w) = \Psi(w)\)，对偶函数等价于对数似然函数，证明最大熵模型学习中的对偶函数极大化等价于最大熵模型的极大似然估计。

这样，最大熵模型的学习问题转换为具体求解对数似然函数极大化或对偶函数极大化的问题。

\[P_w( y \ | \ x) = \frac{exp(\sum_{i=1}^{n} w_i \ f_i(x, y))}{Z_w(x)} \]

\[Z_w(x) = \sum_y exp(\sum_{i=1}^{n} w_i \ f_i(x, y)) \]

最大熵模型表现为以上形式，与logistic回归模型有类似的形式，它们又称对数线性模型。

模型学习的最优化算法

logistic回归模型，最大熵模型的学习以似然函数为目标函数的最优化问题，通常通过迭代算法求解。从最优化观点看，这时的目标函数具有很好的性质，它是光滑的凸函数，因此多种最优化方法都使用，保证能找到全局最优解。

常用的方法有改进的迭代尺度法，梯度下降法，牛顿法或拟牛顿法。牛顿法或拟牛顿法一般收敛速度更快。