排序算法系列之快速排序 (5)
一、普通快速排序
- 快速排序把原数组划分为2个数组,其中左边第一个数组的元素都比选定的关键字小,右边的第二个数组都比选定的关键字大;
- 快速排序采用的是分治的思想:把一个规模大而复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。
- 快速排序的关键在于:选择边界关键值,使得每个左边的数都小于关键值,每个右边的数都大于关键值,快速排序是选择n个关键值的过程.
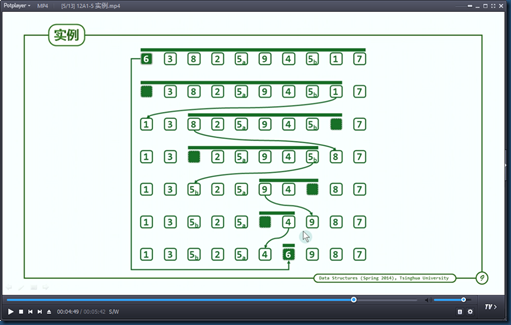
- 快速排序理解:
- 在第一轮排序过程中,原数组的全部数据是一个无序数组M,无序数组最左侧元素i,最右侧元素j,想象左右分别为L和R的有序空数组;
- 选择首位元素值为边界关键字boundKey,然后从无序数组j最右侧依次向左遍历,
- 如果找到大于边界数值boundKey的值,则j -- (表示右侧有序数组R添加了一个元素,中间无序数组M减少了一个元素)
- 直到找到一个元素,使得data[j] < boundKey,此时boundKey为data[i = 0] = boundKey的值,两个数据交换 data[j] <==> data[i],这时候,选定的边界关键字到了j的位置,而比boundKey小的值到了data[i]的位置;
- 一次交换以后,反过来从靠近i的右侧元素i+1位置开始跟 在data[j] 位置的boundKey进行数值比较,如果data[i] 小于BoundKey,则i ++(表示左侧有序数组L添加了一个元素,中间无序数组减少了一个元素)
- 直到找到data[i] > BoundKey,此时boundKey在位置data[j]上,把data[j] <==>data[i] 互换,这时候,选定的关键字到了i的位置,而比boundKey大的值data[i]已经移动到了data[j]上
- 左右循环一次以后,i和j都向中间压缩,直到 i = j 的时候,边界关键字 boundKey左边的值data[0] –> data[i] 都比boundKey小,右侧的值 data[j] –> data[n]都比boundKey大,满足要求;
- 此时boundKey位置已经确定,使用分治的思维,把[0] –> data[i -1] 到data[j +1] –> data[n] 看做两个全新的无序数组,把它们分别进行各自的选择关键值,各自又拆分成新的两个数组进行快速排序
- 直到子数组的元素subArray.count = 1 的时候,不能进行再拆分,分治结束,把全部子数组按顺序排列起来,就是原数组排序后的结果
代码如下:
#region QuickSort快速排序 /// <summary> /// 快速排序 /// </summary> /// <param name="datas"></param> public void QuickSort<T>(T[] datas) where T:IComparable<T> { QRecursionSort(datas, 0, datas.Length - 1); } // 快速排序内部递归函数 :(无序数组,快排起始位置,快排结束位置)// private void QRecursionSort<T>(T[] datas, int iBeginPos, int iEndPos) where T :IComparable<T> { if (datas == null || iBeginPos >= iEndPos || iEndPos >= datas.Length && iBeginPos < 0) return; if (iBeginPos < iEndPos) { int boundPos = QSplit(ref datas, iBeginPos, iEndPos); QRecursionSort(datas, iBeginPos, boundPos - 1); QRecursionSort(datas, boundPos + 1, iEndPos); } } /******************************************************** *函数名称:Split *参数说明:datas 无序数组; * iBegin为datas需要快速排序的起始位置 * iEnd为datas需要快速排序的结束位置 *函数返回:分割后的分割数位置 *说明: 以iBegin处的数值value作为分割数, 使其前半段小于value,后半段大于value *********************************************************/ private int QSplit <T>(ref T[] datas, int iBegin, int iEnd) where T:IComparable<T> { T boundData = datas[iBegin]; // 默认选择子数组第一个数作为边界值进行比较 while (iBegin < iEnd) // 循环切割数组,使得比边界值小的数放数组左边,比边界值大的数放数组右边 { while (iEnd > iBegin && datas[iEnd].CompareTo(boundData) >= 0 ) { iEnd--; } if (iEnd != iBegin) { datas[iBegin] = datas[iEnd]; // 把后方查找到的小与边界值的数据存放在数组首位(边界值之前) iBegin++; while (iBegin < iEnd && datas[iBegin].CompareTo(boundData) <= 0) { iBegin++; } if (iBegin != iEnd) { datas[iEnd] = datas[iBegin]; iEnd--; } } } datas[iEnd] = boundData; return iEnd; } #endregion
- 快速排序还有个缺点就是不稳定性:
- 选择关键字很重要,如果刚好原数组是一个几乎排序好的数组,第一个值恰好是最小或者最大的数,那么就会导致拆分的数组左侧为0或者很小,而右侧很大(反之亦然),那么事件复杂度将会导致T(n) = T(1) + T(n-1) + Θn (其中Θn为最后一次把subArray叠加起来的常数次数),最后导致复杂度为T(n) = O(n)²,那么我们应该怎么解决呢?
- 解决的关键是关键字,我们可以随机选取关键字,就可能会避免这种问题;
public void QuickSortRandom<T>(T[] datas, int beginPos, int endPos) where T : IComparable<T> { if (datas == null || beginPos >= endPos || endPos >= datas.Length && beginPos < 0) return; if (beginPos < endPos) { int boundPos = SplitRandom(ref datas,beginPos,endPos); QuickSortRandom<T>(datas, beginPos, boundPos - 1); QuickSortRandom<T>(datas, boundPos + 1, endPos); } } private int SplitRandom<T>(ref T[] datas, int beginPos, int endPos) where T : IComparable<T> { int lowest = beginPos; int highest = endPos; T boundData = datas[lowest]; //随机快速排序关键在于边界锚点的选定 while (lowest < highest) { // 如果数据比边界锚点大,右侧(小)R序列+1个元素,highest下表左移,中间无序数组元素-1 for (; highest > lowest && datas[highest].CompareTo(boundData) >= 0; ) { highest--; } if (highest != lowest) { datas[lowest] = datas[highest]; lowest++; // 如果数据比边界锚点小,左侧(小)L序列+1个元素,lowest下表左移,中间无序数组元素+1 for (; lowest < highest && datas[lowest].CompareTo(boundData) <= 0; ) { lowest++; } if (lowest != highest) { datas[highest] = datas[lowest]; datas[lowest] = boundData; highest--; } } } datas[highest] = boundData; return highest; }