排序算法系列之选择排序 (2)

一、选择排序

1. 选择排序原理:在长度为nd 数组中,找到位置不适合的元素,直接放入最终合适的位置上,也就是依次在未排序数组中找到最小元素,,直到最后一个元素位置(剩下的最后一个元素n-2最大,无需操作)
2. 每轮从无序数组中找到的最小数据,依次放入到从data[0]到data[n-2]中;
3. 优点:赋值次数少
4. 缺点:忽略了数据已经在适合的位置上,不需要交换的情况

public  void SelectionSort<T>(T[] datas) where T: IComparable<T>  
    {
        int mins;
        int tamp;

        for (int i = 0, j, index; i < datas.Count() - 1; i++)
        {
            mins = datas[i];
            index = i;
            for (j = i; j < datas.Count(); j++)
            {
                if (datas[j] < mins)
                {
                    mins = datas[j];  // 无谓的数据交换,抛弃
                    index = j;
                }
            }
            tamp = mins;
            datas[index] = datas[i];
            datas[i] = mins;
        } 
    }

/// <summary>
    /// 选择排序 ：从左到右找到数据中最小的数,进行多次,每次最小的分别与第一,第二...个元素进行直接交换,直到最n-2(最后一次不需要排序)
    /// </summary>
    public  void SelectionSort<T>(T[] datas) where T: IComparable<T>  
    {
        if (datas == null) return;

        for (int i = 0,j,least; i < datas.Count()-1; i++)
        {
            for ( j = i+1,least = i; j < datas.Count(); j++)
            {
                if (datas[j].CompareTo(datas[least]) < 0)
                {
                    least = j;
                }
            }
            if (least != i)
            {
                Swap(ref datas[i],ref datas[least]);
            }
        }
    }

 

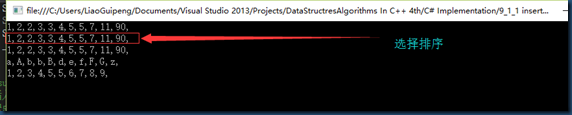
测试数据:

int[] selectionDatas = { 5, 7, 3, 5, 2, 11, 90, 4, 2, 1, 3 };

        program.SelectionSort(selectionDatas);
        DebugExtension.DebugArray(selectionDatas);

 

排序结果: