汉诺塔问题递归算法的设计
汉诺塔问题的描述是:设有三根标号为A,B,C的柱子上,在A柱上放着n个盘子,每一个都比下面的略小一点,要求把A柱上的盘子全部移动到C柱上,规则是:一次只能移动一个盘子;移动的过程中大盘只能放在小盘下面;在移动过程中盘子可以放在A,B,C的任意一个柱子上。
递归方法求解:一个盘子的汉诺塔问题可直接移动(递归出口)。n个盘子的汉诺塔问题可递归表示为如下的子问题求解的形式,首先把上边的n-1个盘子从A柱移动到B柱,然后把最下边的一个盘子从A柱移动到C柱,最后把移到B柱的n-1个盘子再移到C柱。
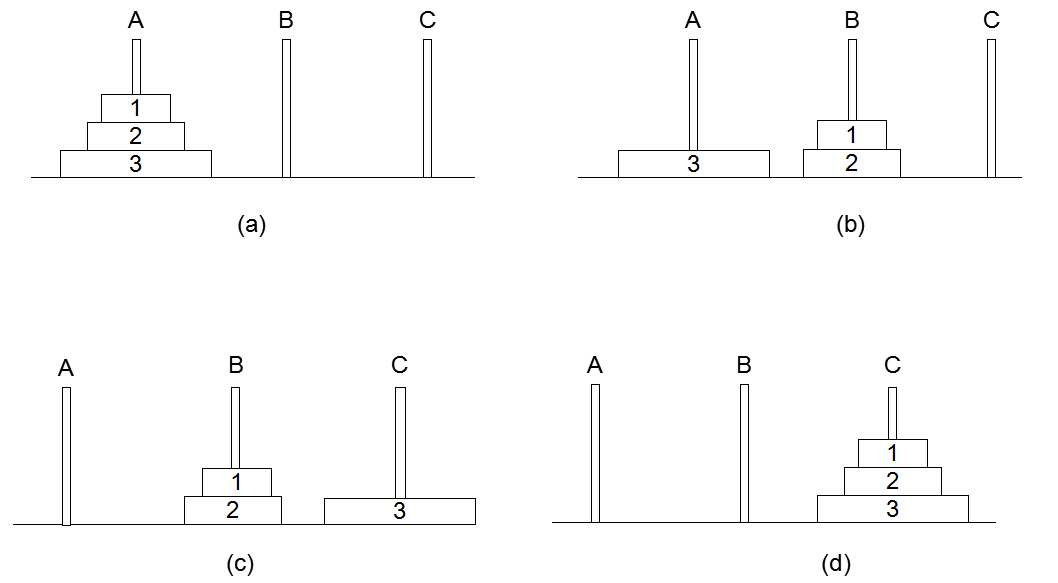
如下图所示,n个盘子从上到下标号为1,2,3,4,……,n
1 package tower; 2 3 public class Tower { 4 public static void moveDish(int n, char from, char temp, char to) { 5 if (n == 1) { 6 System.out.println( "1 号 : " +"from " +from +" to "+ to); 7 } else { 8 moveDish(n - 1, from, to, temp); 9 System.out.println(n + " 号 : "+ "from " + from + " to " + to); 10 moveDish(n - 1, temp, from, to); 11 } 12 } 13 14 public static void main(String []args){ 15 moveDish(3, 'A', 'B', 'C'); 16 } 17 }