判断线性无关的办法，以及线性相关或者线性无关的笔记截图

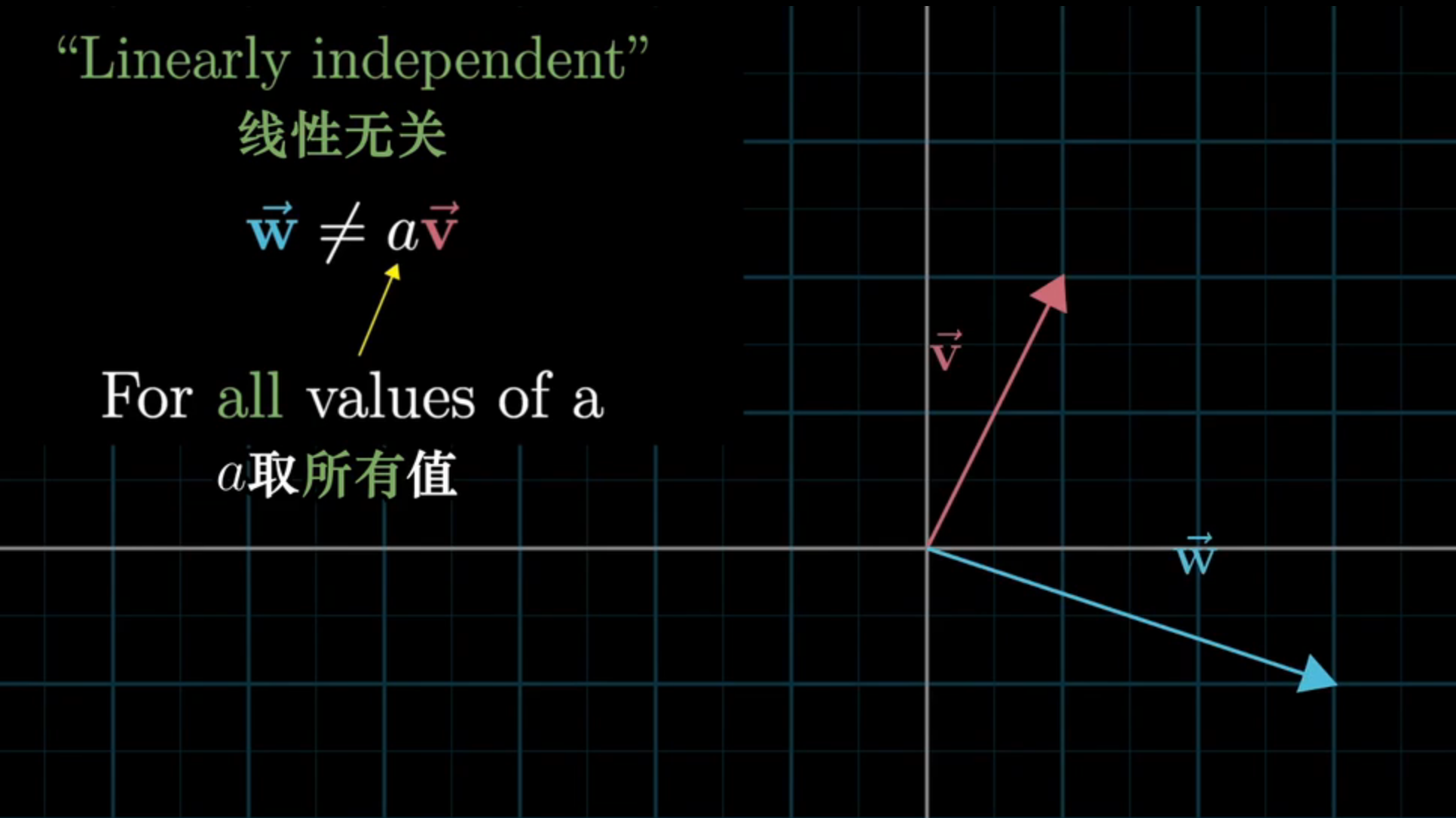
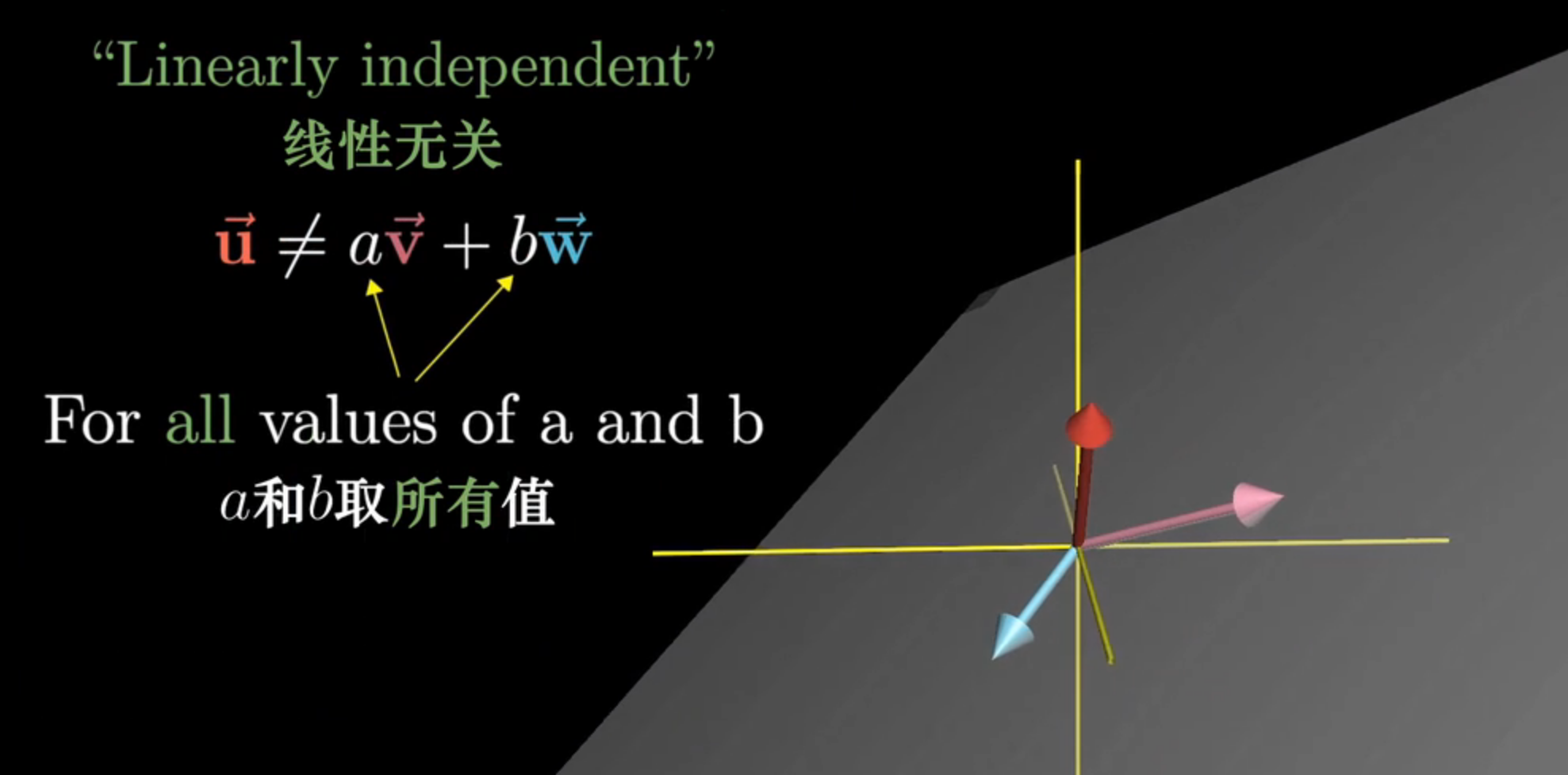
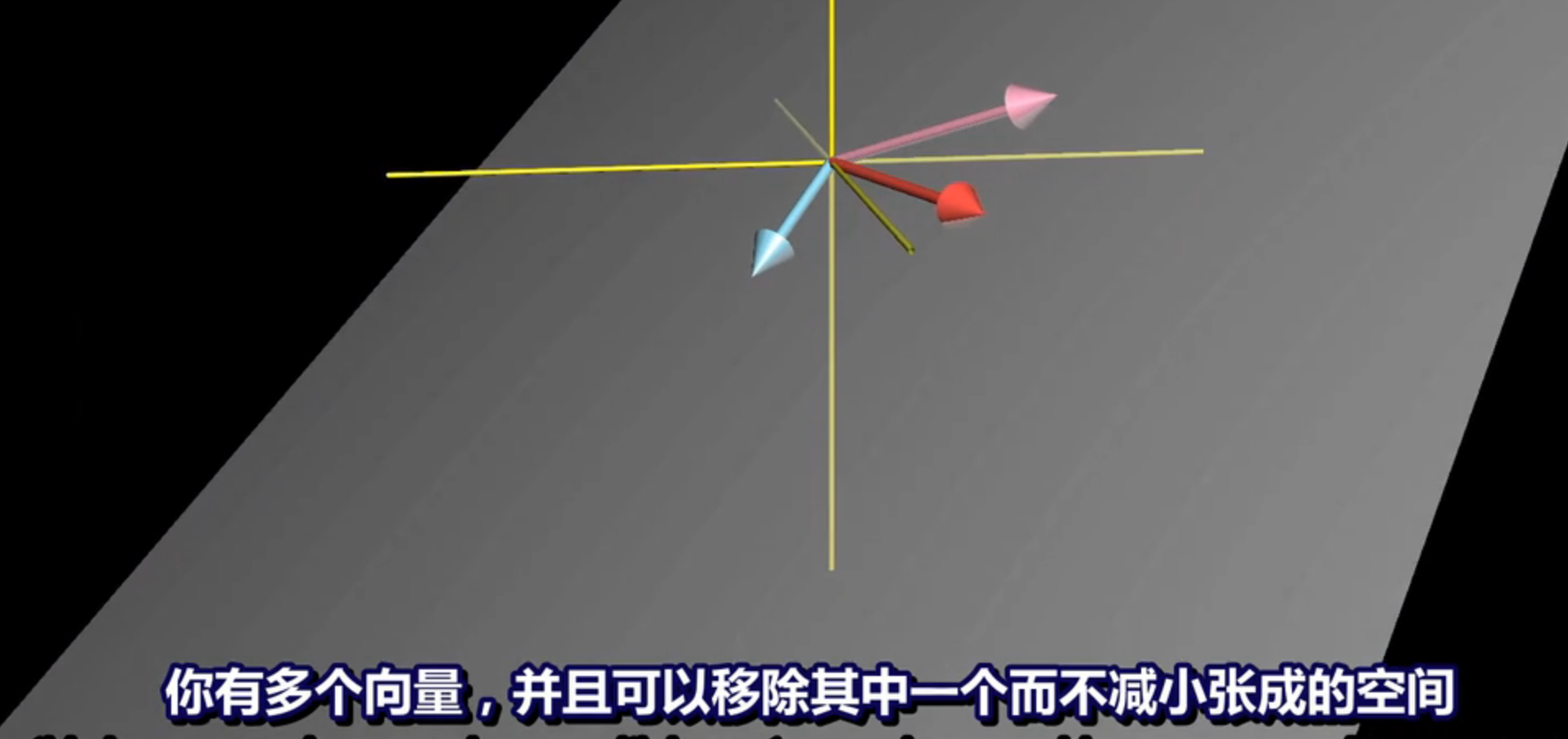
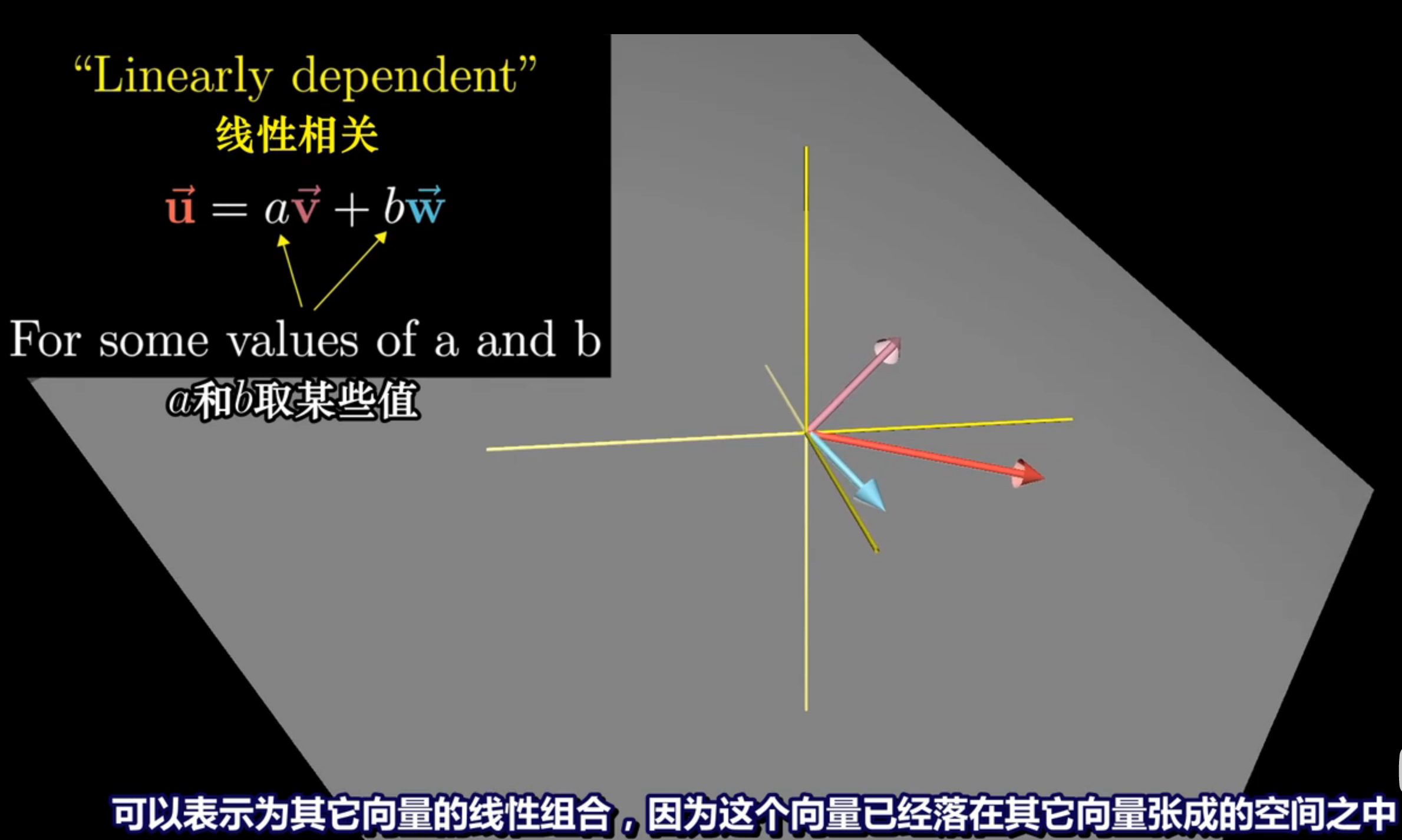
线性无关性是向量组中一个非常重要的概念。如果一个向量组是线性无关的，那么它的每个向量都不能表示成其余向量的线性组合，而只能表示成自身的线性组合。

有很多方法来判断一个向量组是否线性无关，其中一种常用的方法是：检查向量组的行列式是否为零。

具体来说，一个向量组\(v_1,v_2,\ldots,v_n\)是线性无关的，当且仅当它们构成的矩阵的行列式不等于零，即：

\[\det\begin{pmatrix}v_1 & v_2 & \cdots & v_n \end{pmatrix} \neq 0 \]

如果行列式为零，则向量组线性相关，否则线性无关。

例如，对于向量组\({\bf v_1} = \begin{pmatrix}1 \\ 0 \\ 0 \end{pmatrix}, {\bf v_2} = \begin{pmatrix}0 \\ 1 \\ 0 \end{pmatrix},{\bf v_3} = \begin{pmatrix}0 \\ 0 \\ 1 \end{pmatrix}\)，可以构造如下的行列式：

\[\det\begin{pmatrix}{\bf v_1} & {\bf v_2} & {\bf v_3}\end{pmatrix} = \det\begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}=1\cdot 1\cdot 1 =1 \]

因此，可以得出结论，向量组\({\bf v_1, v_2, v_3}\)是线性无关的。

需要注意的是，此方法只适用于有限维向量空间中的向量组。在无限维向量空间中，有时需要使用其他的方法来判断向量组的线性无关性。

---

---

---

---

---

除了行列式法之外，还有其他的方法来判断向量组是否线性无关。其中一个方法是利用向量组的线性表示来判断它们是否线性无关。

假设有向量组\(v_1,v_2,\ldots,v_n\)，则对于任意的实数\(c_1,c_2,\ldots,c_n\)，如果以下线性方程组：

\[c_1{\bf v_1}+c_2{\bf v_2}+\cdots+c_n{\bf v_n} = {\bf 0} \]

只有\(c_1=c_2=\cdots=c_n=0\)时有解，则向量组\(v_1,v_2,\ldots,v_n\)是线性无关的。否则，如果存在\(c_1,c_2,\ldots,c_n\)中至少有一个不为零，使得该线性方程组有解，则向量组\(v_1,v_2,\ldots,v_n\)是线性相关的。

例如，在向量空间\(\mathbb{R}^3\)中，假设向量组\({\bf v_1}=\begin{pmatrix}1\\0\\0\end{pmatrix}, {\bf v_2}=\begin{pmatrix}2\\1\\0\end{pmatrix}, {\bf v_3}=\begin{pmatrix}4\\-1\\1\end{pmatrix}\)，判断这个向量组是否线性无关。

对于任意的\(c_1,c_2,c_3\)，线性方程组\(c_1{\bf v_1}+c_2{\bf v_2}+c_3{\bf v_3}={\bf 0}\)可以写成矩阵方程组的形式：

\[\begin{pmatrix}1 & 2 & 4 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}c_1 \\ c_2 \\ c_3\end{pmatrix}=\begin{pmatrix}0 \\ 0 \\ 0\end{pmatrix} \]

通过高斯消元法或矩阵求逆的方法，可以求出该矩阵的逆矩阵：

\[\begin{pmatrix}1 & 2 & 4 \\ 0 & 1 & -1 \\ 0 & 0 & 1 \end{pmatrix}^{-1}=\begin{pmatrix}1 & -2 & -2 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix} \]

因此，如果\(c_1{\bf v_1}+c_2{\bf v_2}+c_3{\bf v_3}={\bf 0}\)，则有:

\[\begin{pmatrix}c_1 \\ c_2 \\ c_3\end{pmatrix}=\begin{pmatrix}1 & -2 & -2 \\ 0 & 1 & 1 \\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix}0 \\ 0 \\ 0\end{pmatrix}={\bf 0} \]

因此，向量组\({\bf v_1,v_2,v_3}\)是线性无关的。

---

---

---

另外还有一种3b1b up所讲的