数理统计笔记
常见的分布函数
二项分布

几何分布

超几何分布

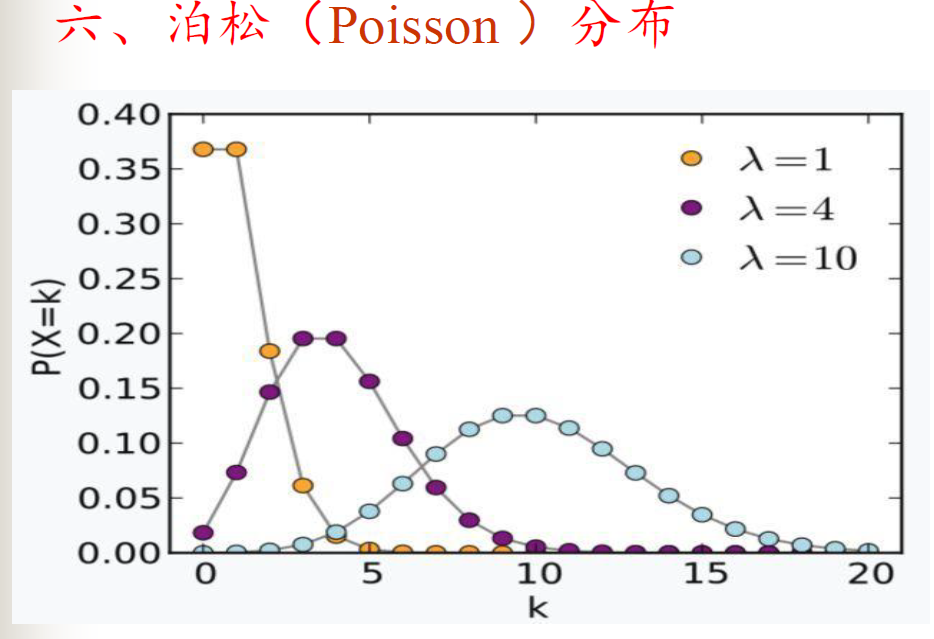
泊松分布

均匀分布

指数分布

正态分布

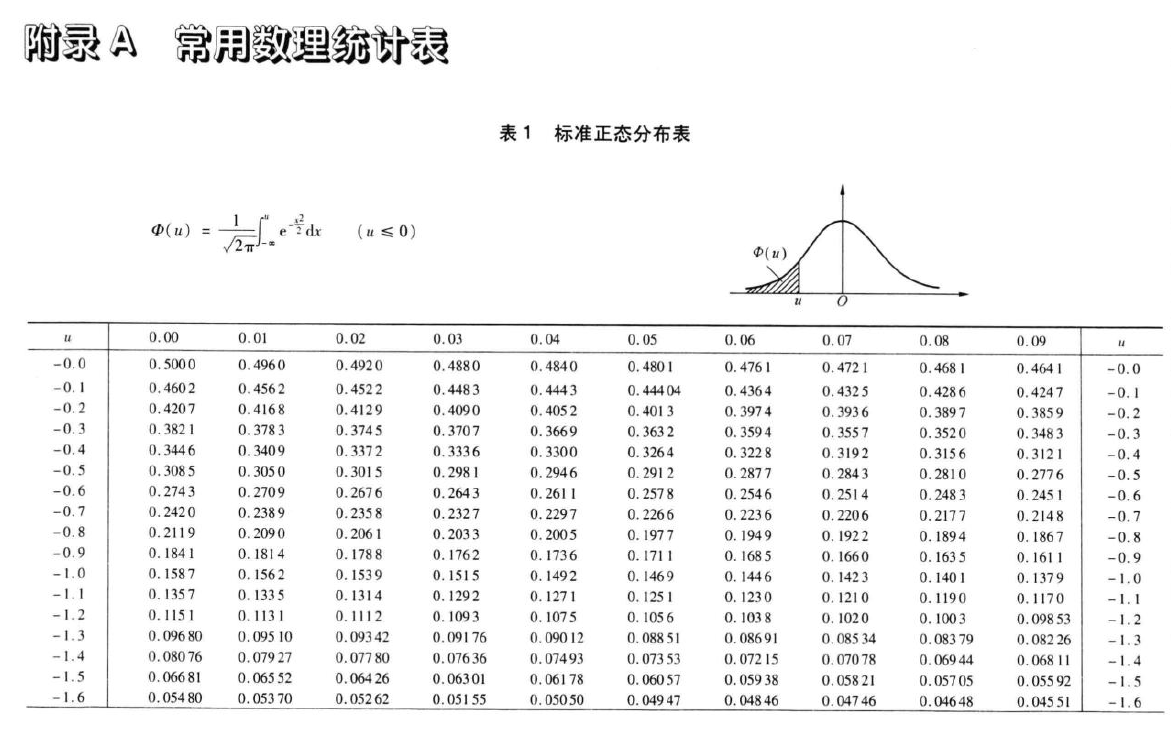
标准正态分布


二项分布和泊松分布之间的关系
泊松分布可以看作是二项分布的一种极限形式。当考虑一个二项分布问题,如果试验次数𝑛非常大,而每次试验成功的概率𝑝非常小,但乘积𝑛𝑝(期望值)保持在一个有限的常数𝜆,这时二项分布就可以近似为泊松分布。这意味着,在大量独立的伯努利试验中,如果每次试验成功的概率很小,关注的是成功次数而不是每次试验的具体结果时,泊松分布提供了一个更简便的模型。
在上述极限情况下,泊松分布的参数𝜆实际上等于二项分布中成功次数的期望值𝑛𝑝。这表明泊松分布中的事件发生率𝜆可以直接通过二项分布的参数𝑛和𝑝来确定
二项分布、泊松分布、正态分布的特性
其中的二项分布B和泊松分布P具有可加性

正态分布之和的特性

常用函数的期望与方差

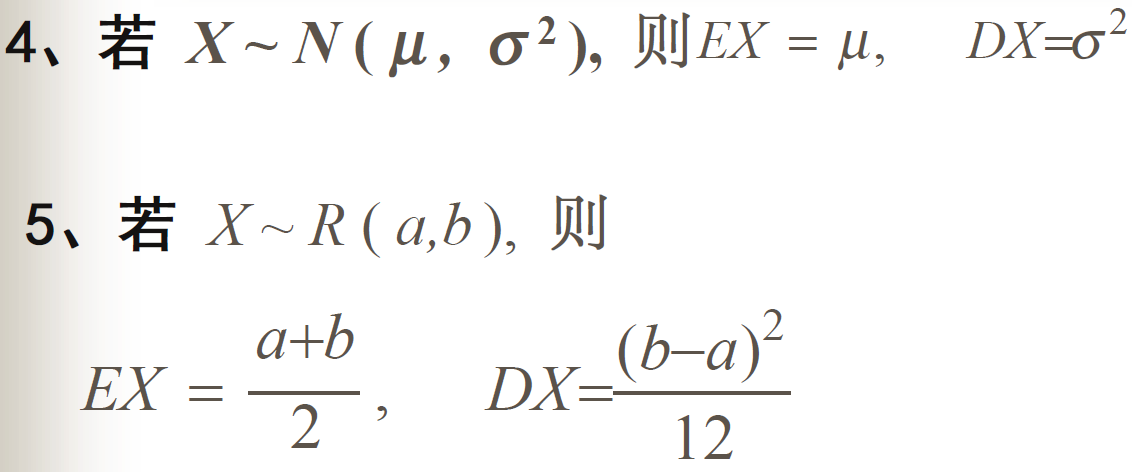
常用分布函数
正态分布

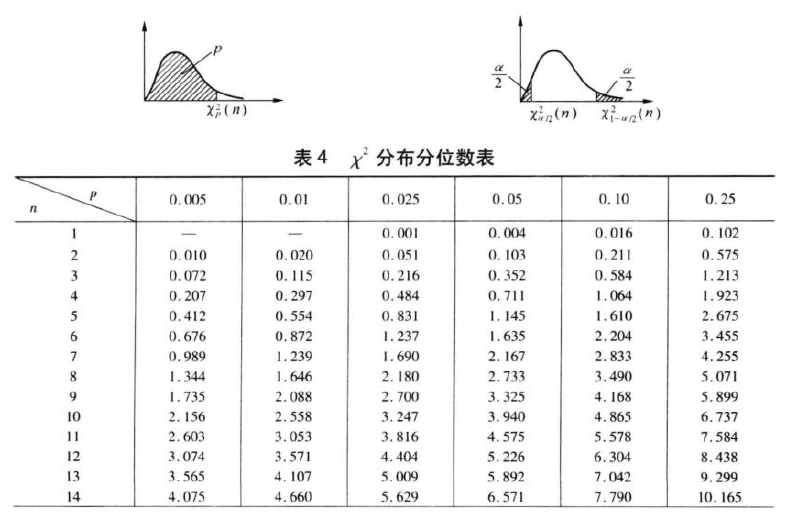
卡方分布
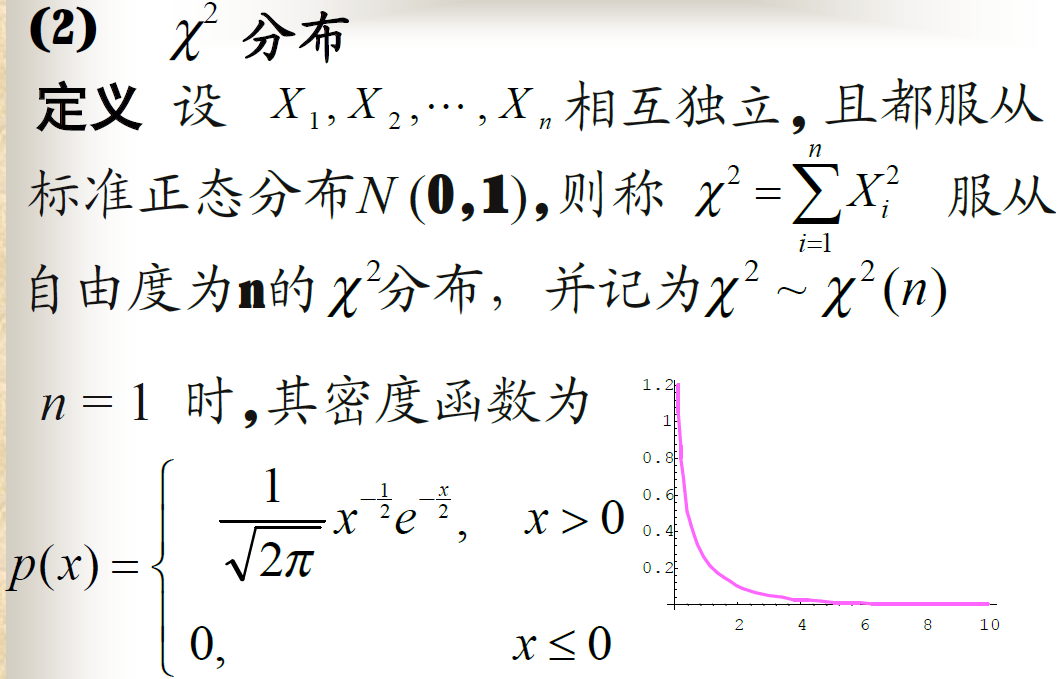
卡方分布的性质

t分布

t分布的性质

F分布

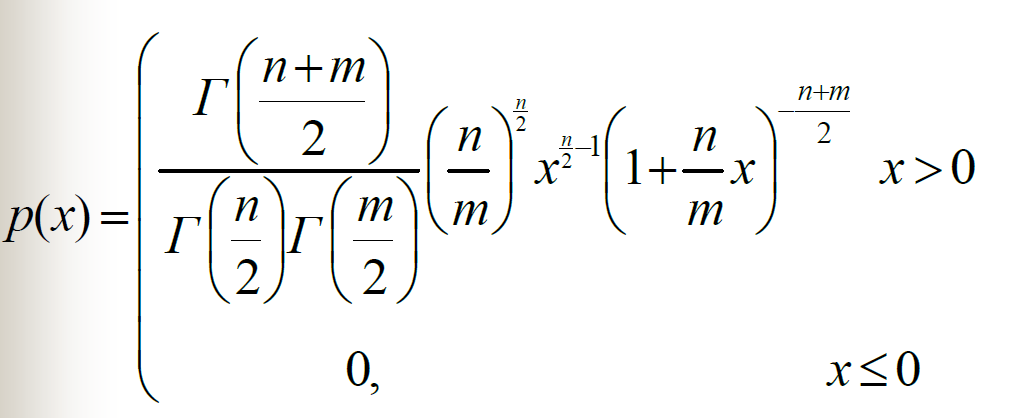
F分布的性质

经典题目
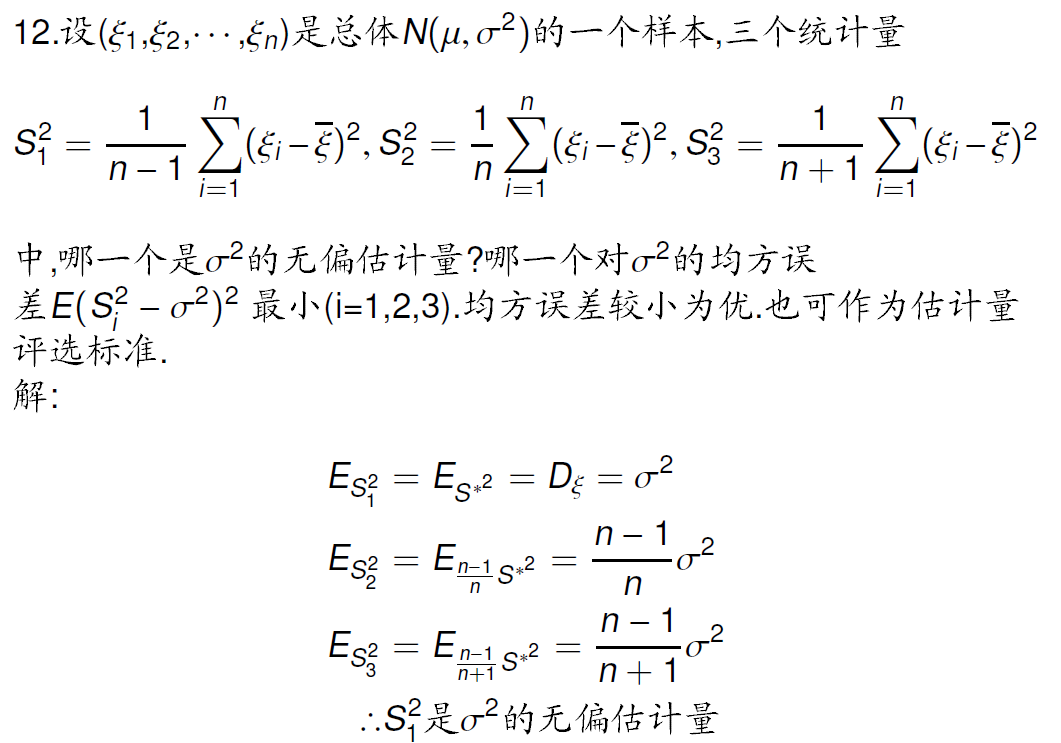
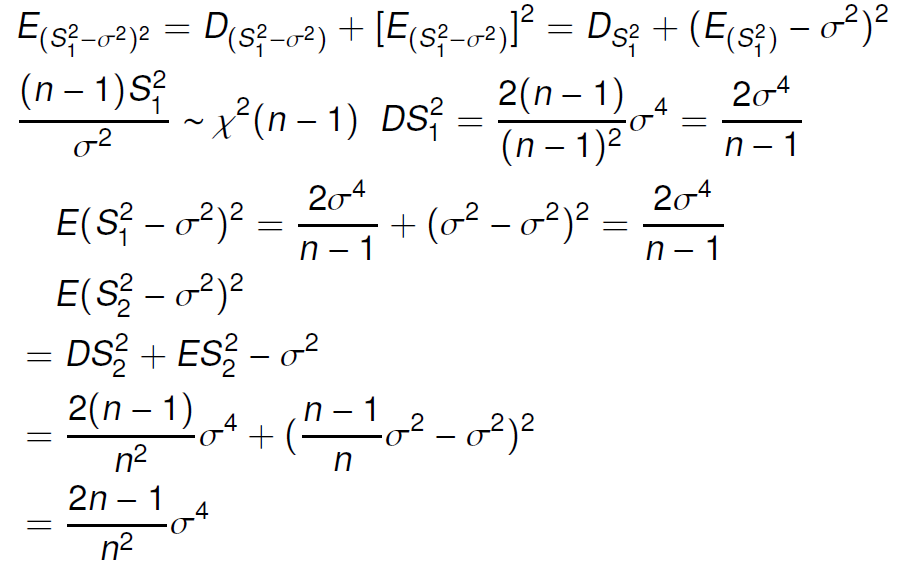

分布函数与密度函数
分布函数的定义
分布函数是指随机变量小于一个数值x的概率,准确来说分布函数应该叫做累计分布函数

通常分布函数采用大写字母F来表示,P表示x点发生的概率
从而可以得出以下的性质

分布函数与密度函数的关系



变量的独立性

独立的变量相加的方差运算

两个变量和的分布

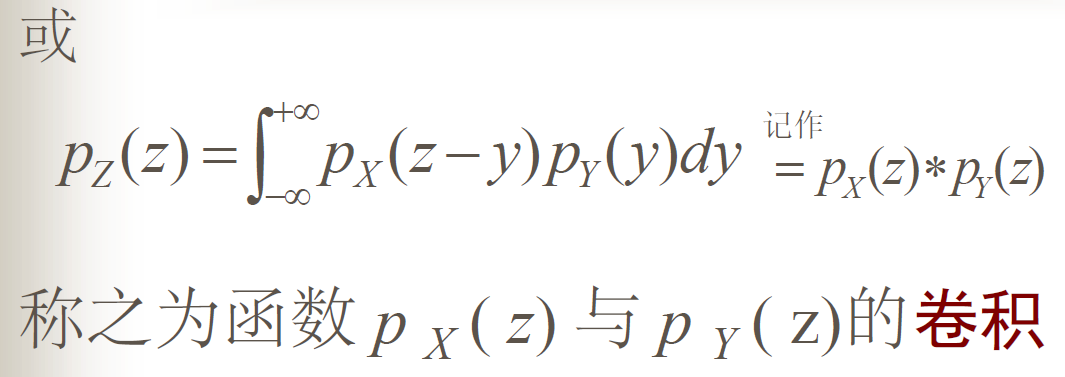
变量和的分布运算方式与卷积类似

K阶原点矩与K阶中心距

原点距可以看成数据点到原点的距离
中心距则是数据到达数据中心点的距离
极差

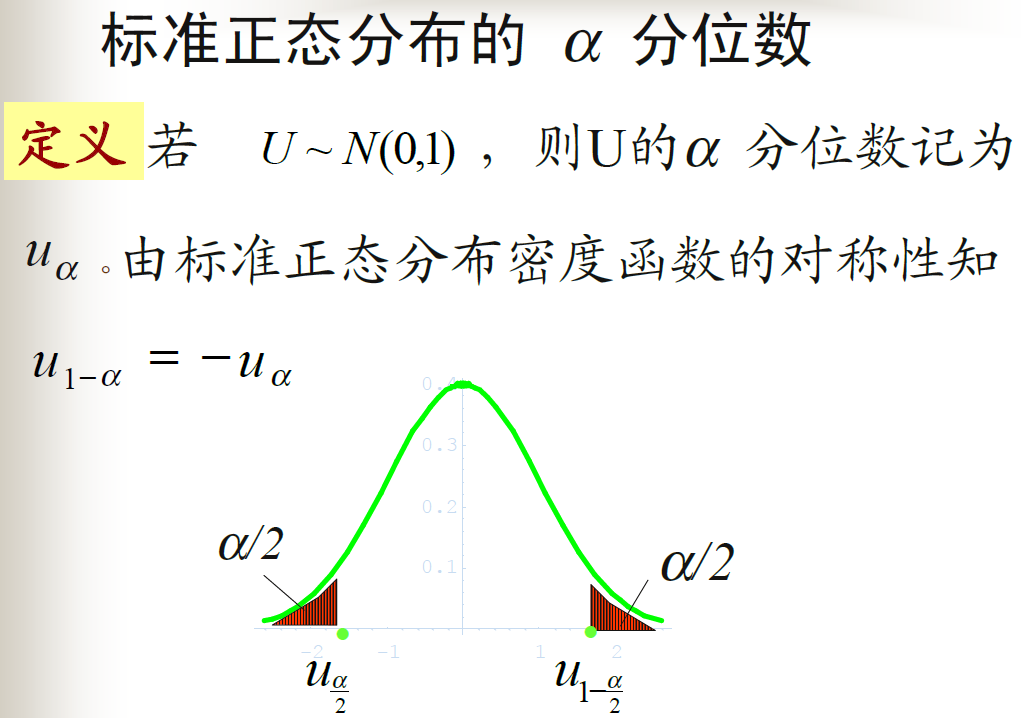
分位数

抽样分布
正态总体的抽样分布

可以看出,抽样后的样本均值符合正态分布,抽样的均值等于总体均值,方差等于总体方差的1/n。
需要注意样本方差与卡方分布的系数中,卡方分布的自由度是n-1


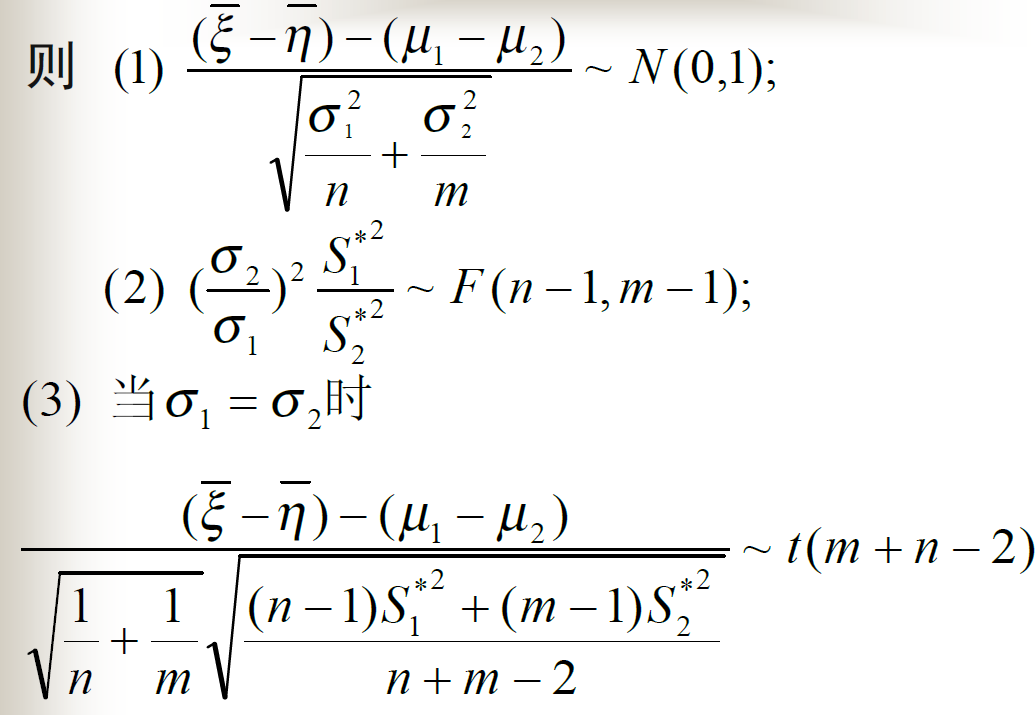

样本均值
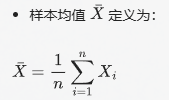
样本无偏方差
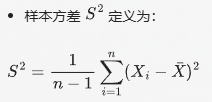
样本均值的期望
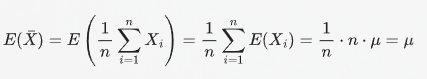
无偏方差的期望


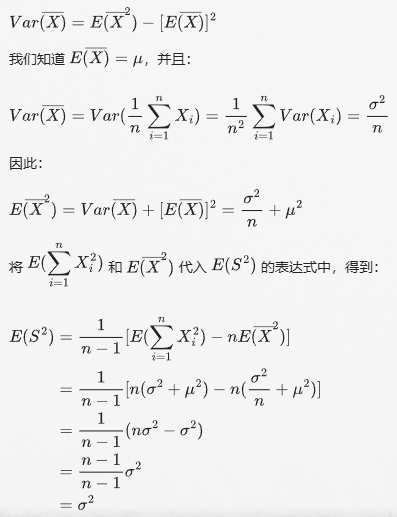
点估计方法
矩法
矩估计是数理统计中一种常用的参数估计方法,它基于总体的矩(如均值、方差等)与参数之间的关系来进行估计。矩估计的基本思想是利用样本矩来估计相应的总体矩,进而通过总体矩与参数的关系来估计未知参数。这种方法直观、简便,并且适用于多种类型的分布。


极大似然估计
极大似然估计(Maximum Likelihood Estimation, MLE)是一种常用的参数估计方法,其核心思想是寻找一组参数值,使得观察到的数据出现的似然性(即概率)最大。换句话说,极大似然估计选择使数据观测值出现概率最大的参数值作为估计值。

顺序统计量法


评价估计量地标准
- 无偏性
- 有效性
- 相合性
无偏性

有效性




相合性

置信区间



单侧置信区间

正态总体参数的置信区间
方差已知,均值的置信区间


方差未知,均值的置信区间

均值已知,方差的置信区间

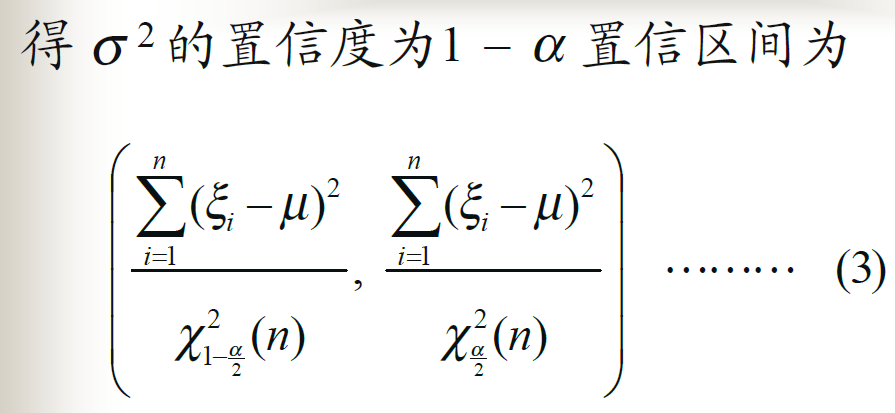
均值未知,方差的置信区间
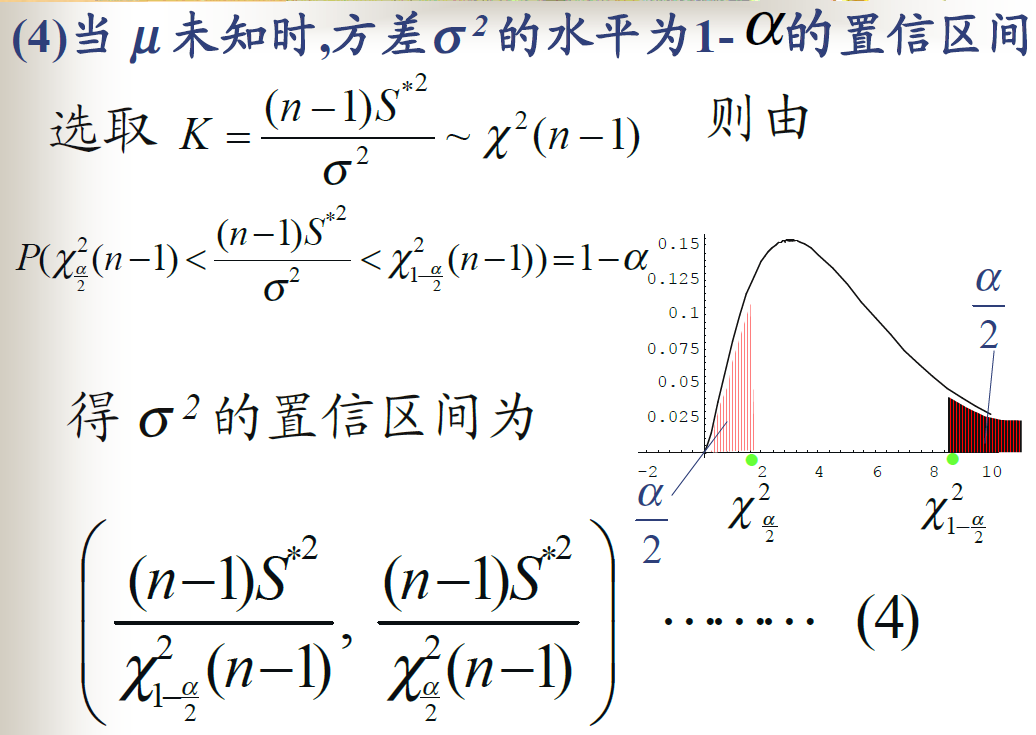
两个正态总体的情况

方差已知,均值的置信区间

方差未知,均值的置信区间


均值已知,方差比的置信区间

均值未知,方差比的置信区间

正态总体均值与方差的联合区间估计


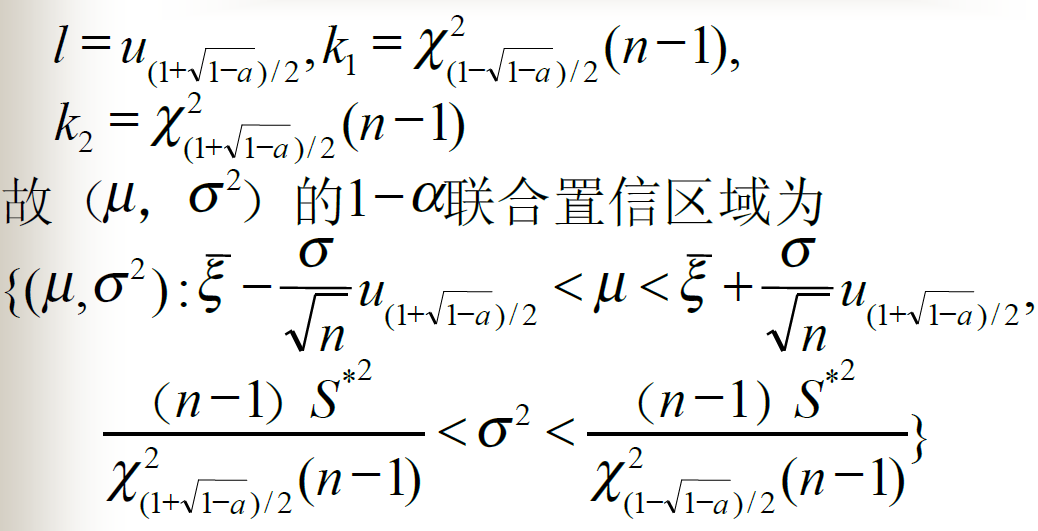
0-1分布的参数区间估计

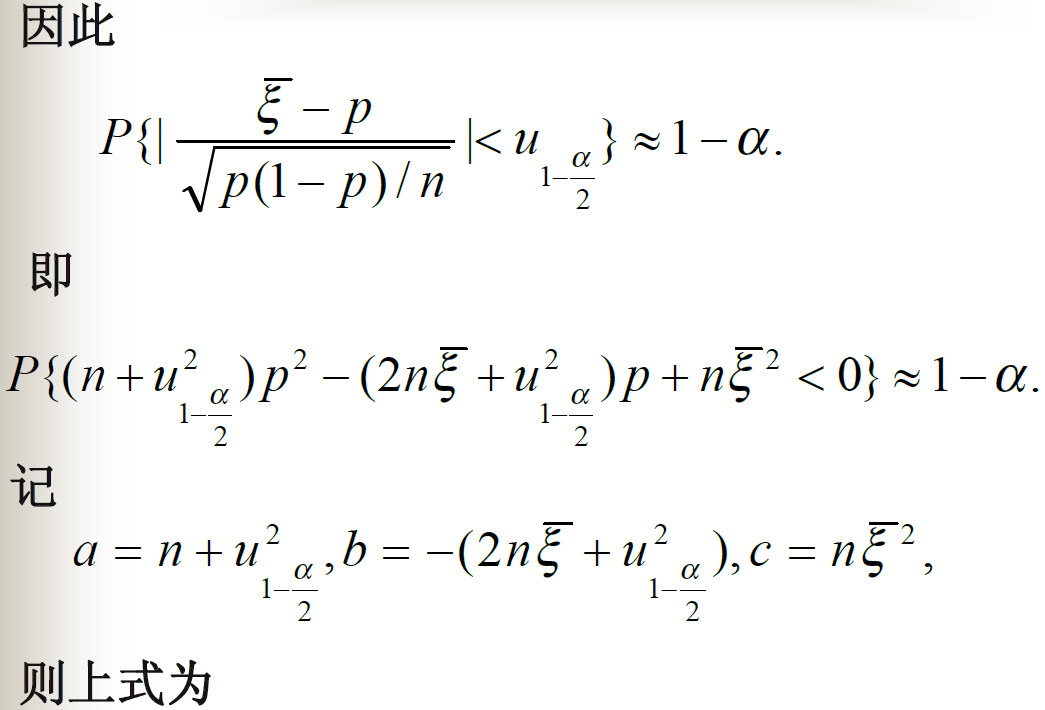



假设检验



检验的显著水平与两类错误



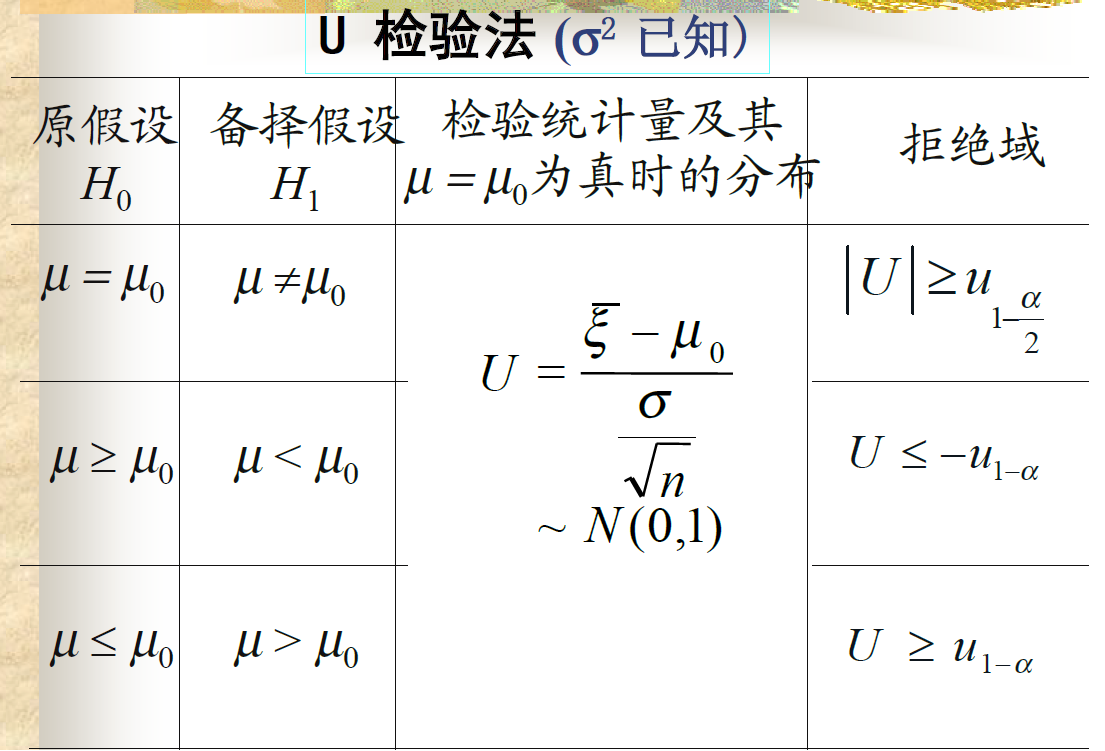
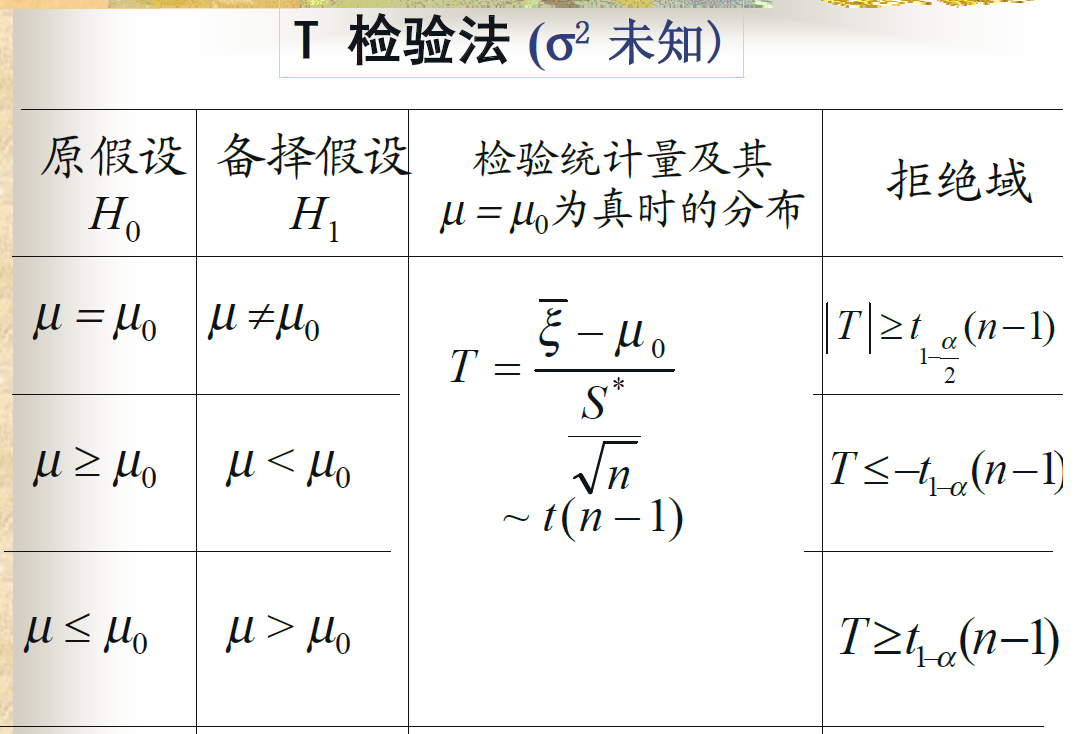
单正态总体的参数假设检验
均值的检验


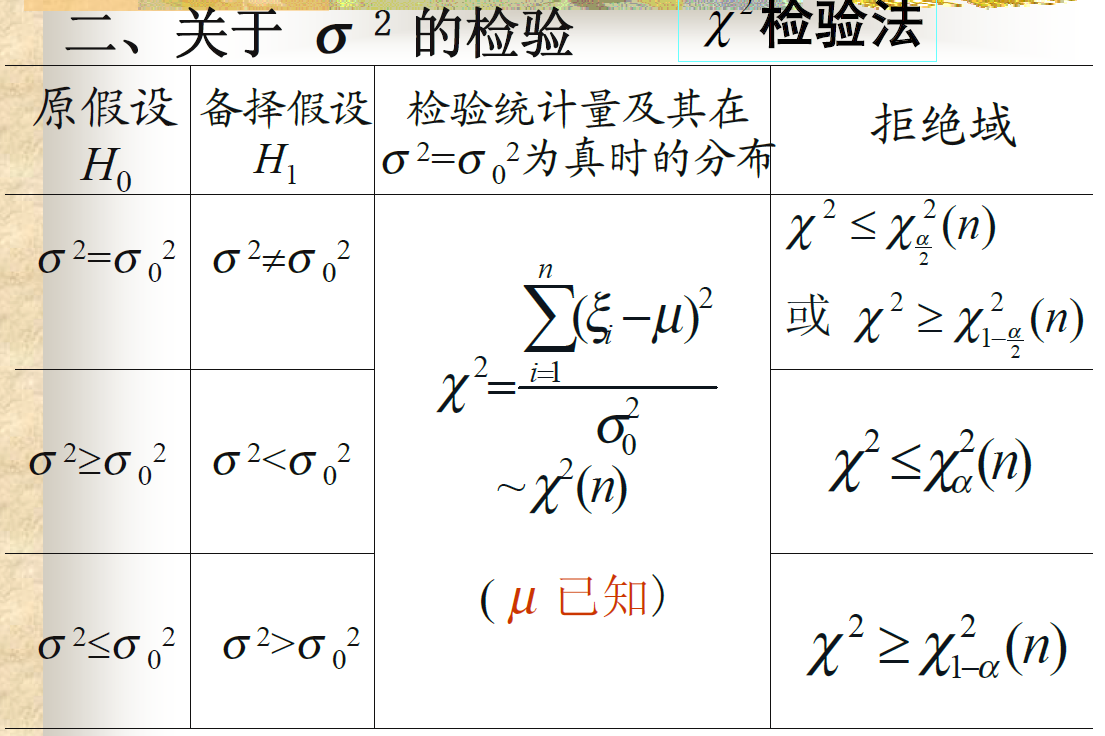
方差的检验

两个正态总体的参数假设检验

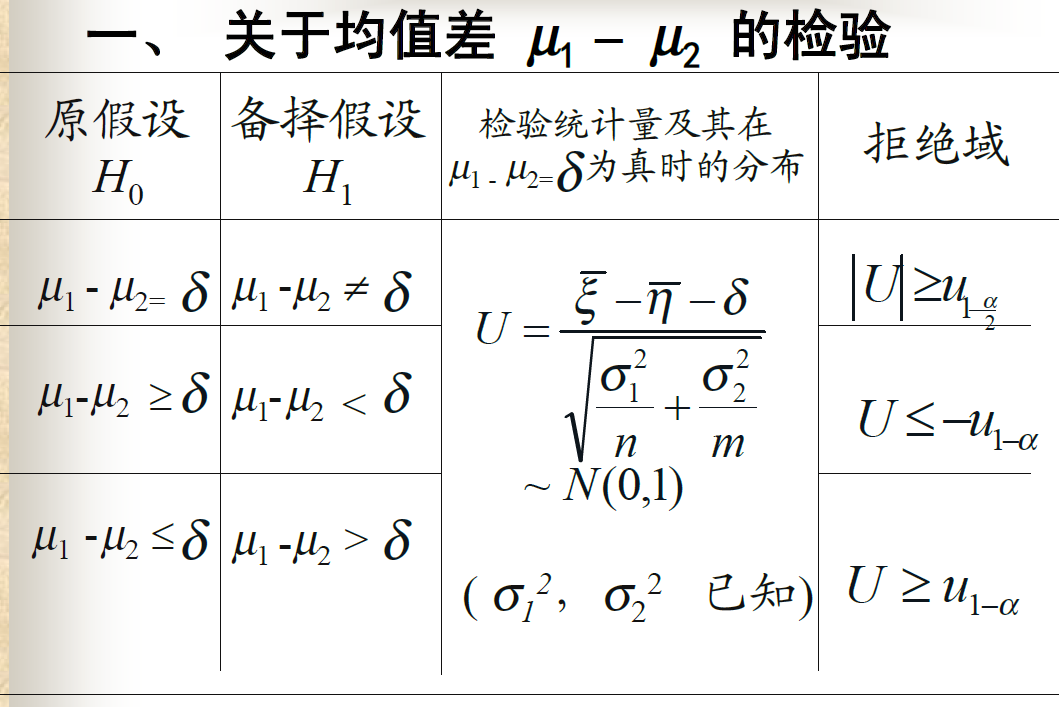
均值差的检验

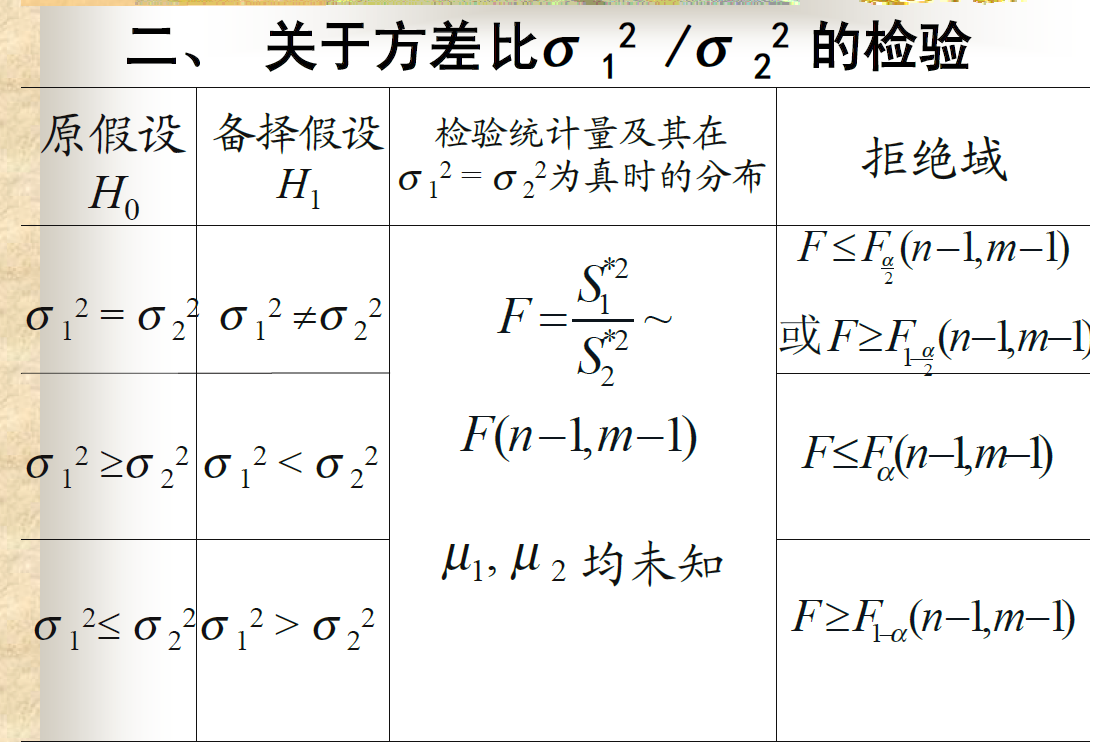
方差比的检验

非正态总体均值的假设检验
方差已知时总体均值的假设检验




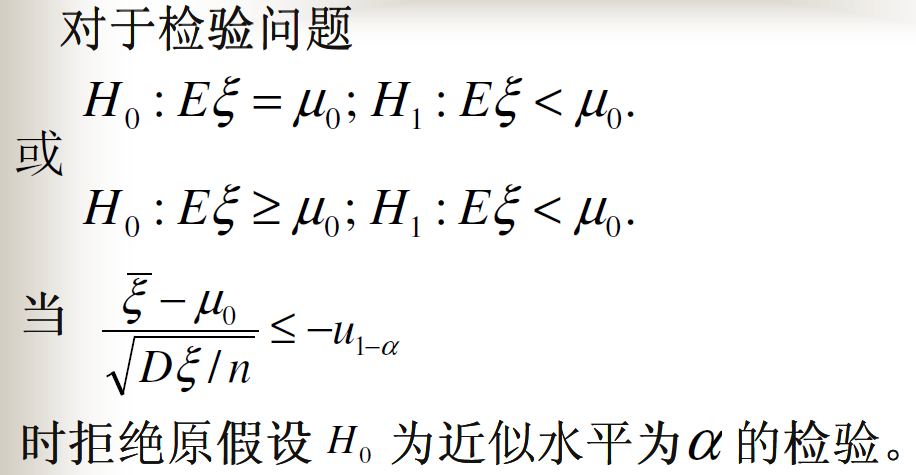
方差未知时总体均值的假设检验



方差已知时两个总体均值的假设

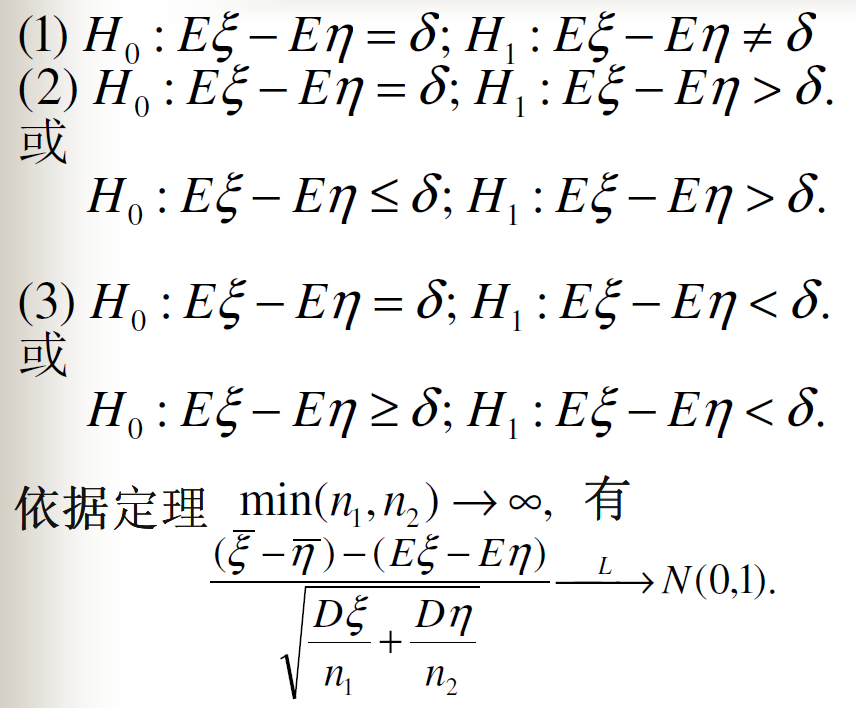

方差未知时两个总体均值的假设


分布拟合检验
卡方检验










独立性检验

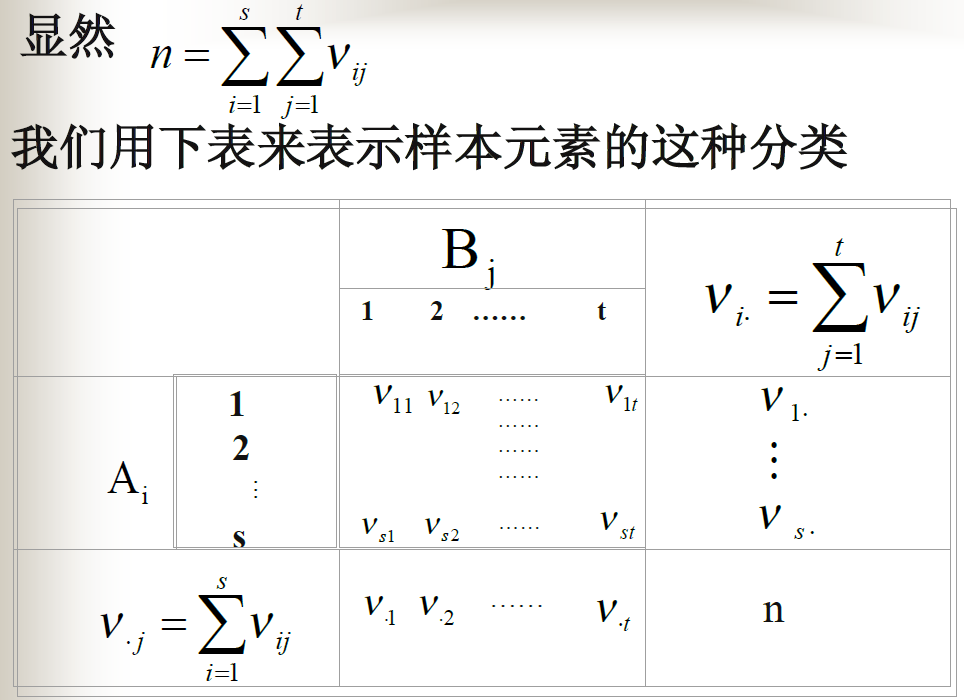



两个总体相等性检验

符号检验法



秩和检验法







游程检验法




回归分析
一元线性回归
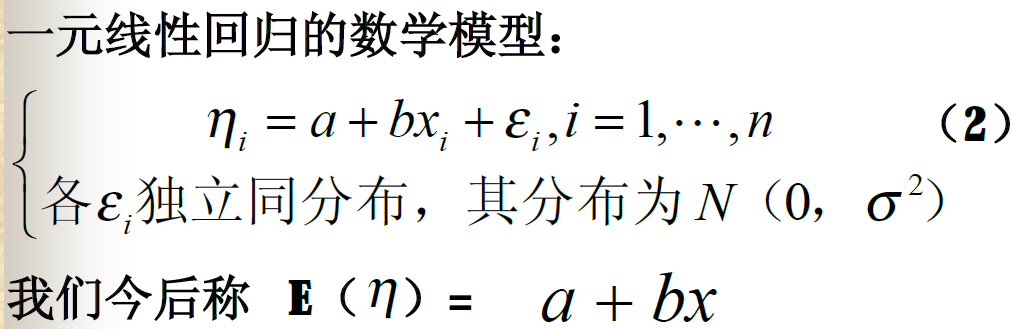

最小二乘法

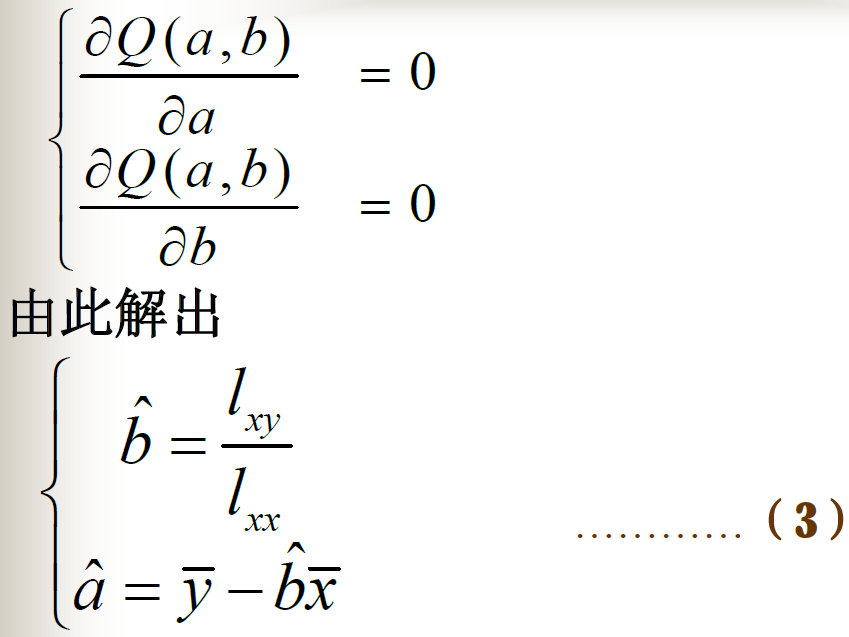


最小二乘法中a,b两个参数计算推导过程
线性回归的基本概念
线性回归模型假定因变量
其中,
最小二乘法的目标
最小二乘法(Ordinary Least Squares, OLS)的目标是找到
定义误差平方和(Sum of Squared Errors, SSE)为:
对
我们通过对
- 对
令其等于零:
- 对
令其等于零:
联立方程求解
得到方程组:
- 先求
记:
则方程组改写为:
利用第二个方程:
代入 ( a = \bar{y} - b \bar{x} ):
整理得:
- 再求
从上面推导出的关系:
最终回归系数公式
通过上述步骤,推导了最小二乘法的线性回归方程中的回归系数 ( b ) 和截距 ( a ) 的公式。
最小二乘法的相关性质

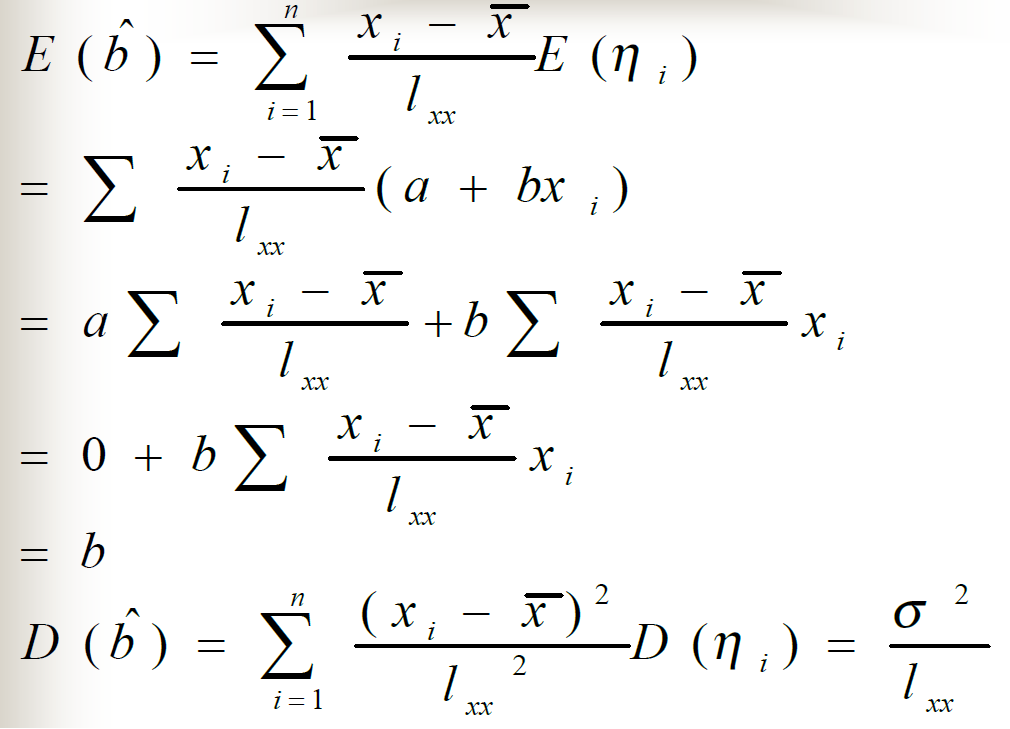

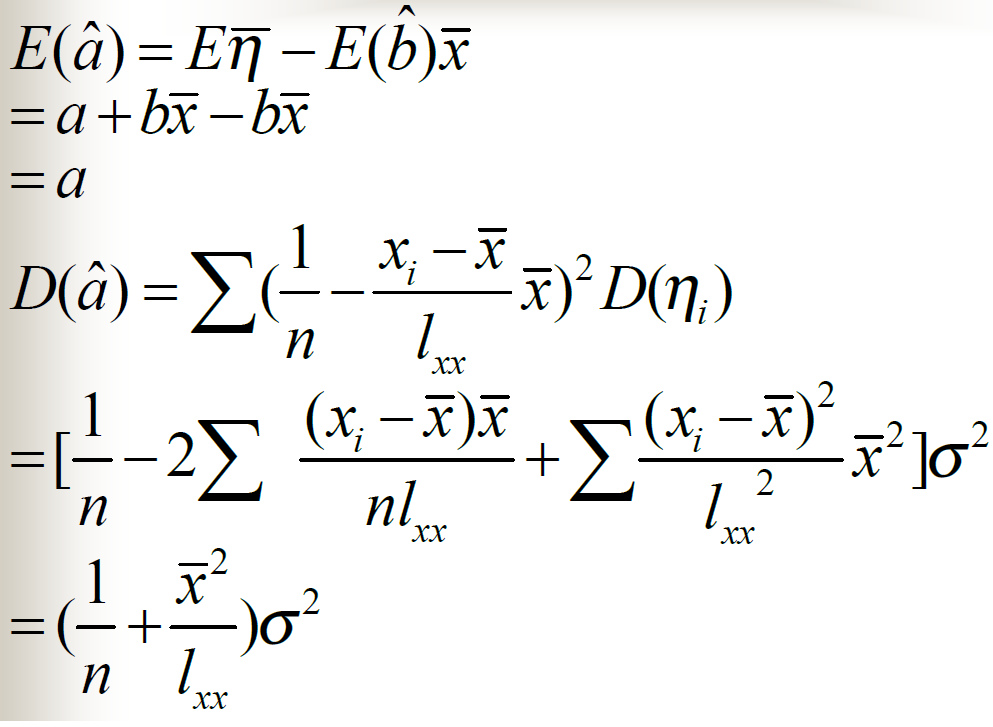
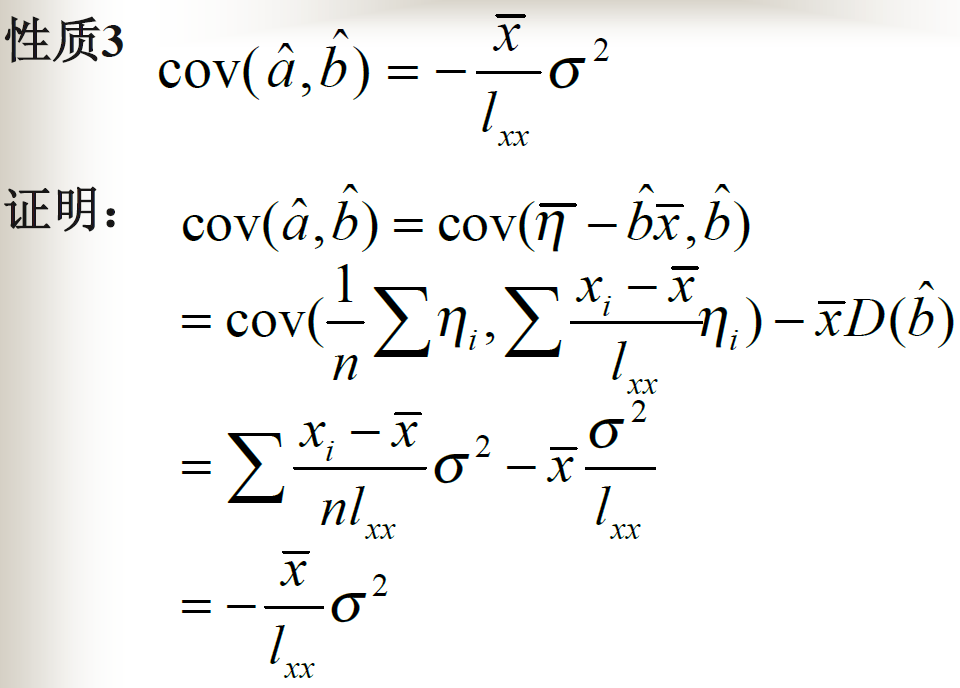

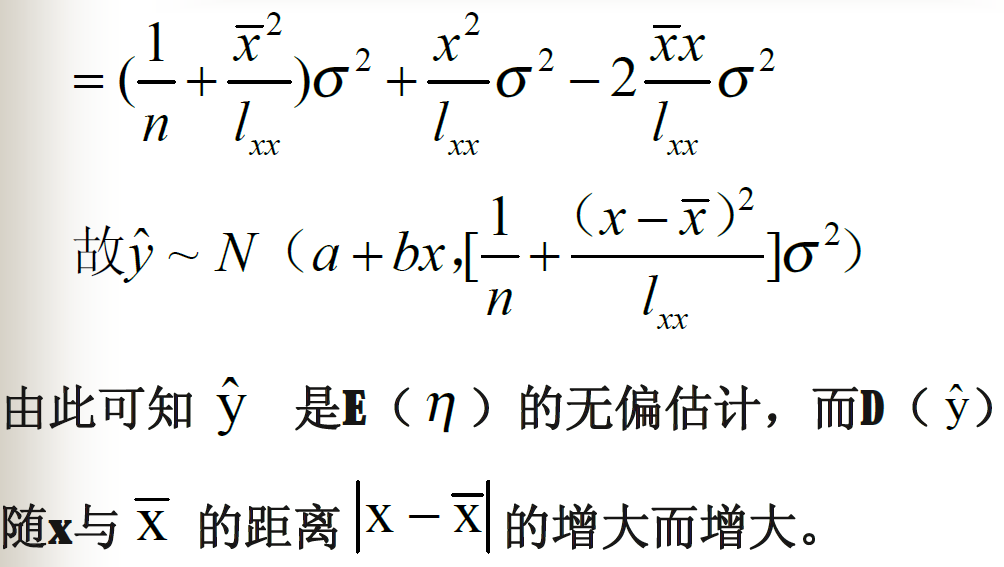
线性回归效果显著性检验




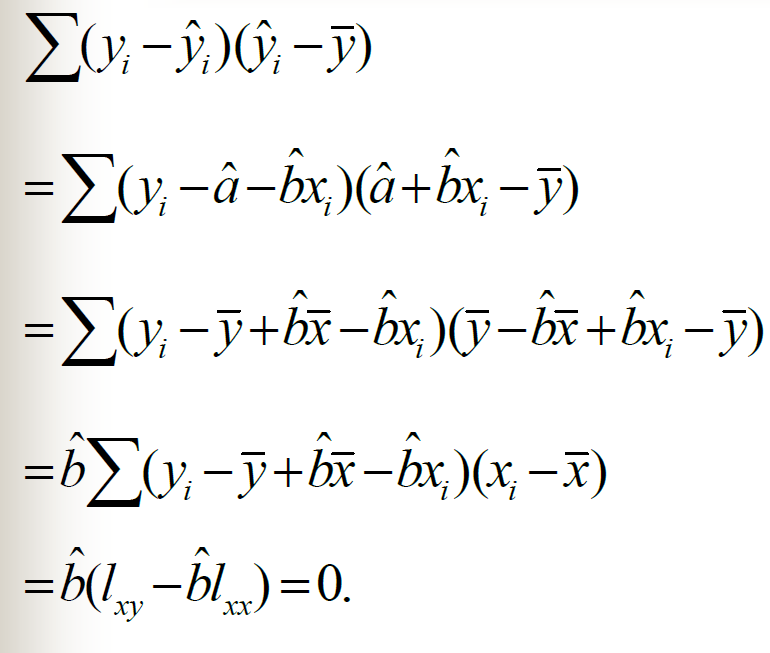
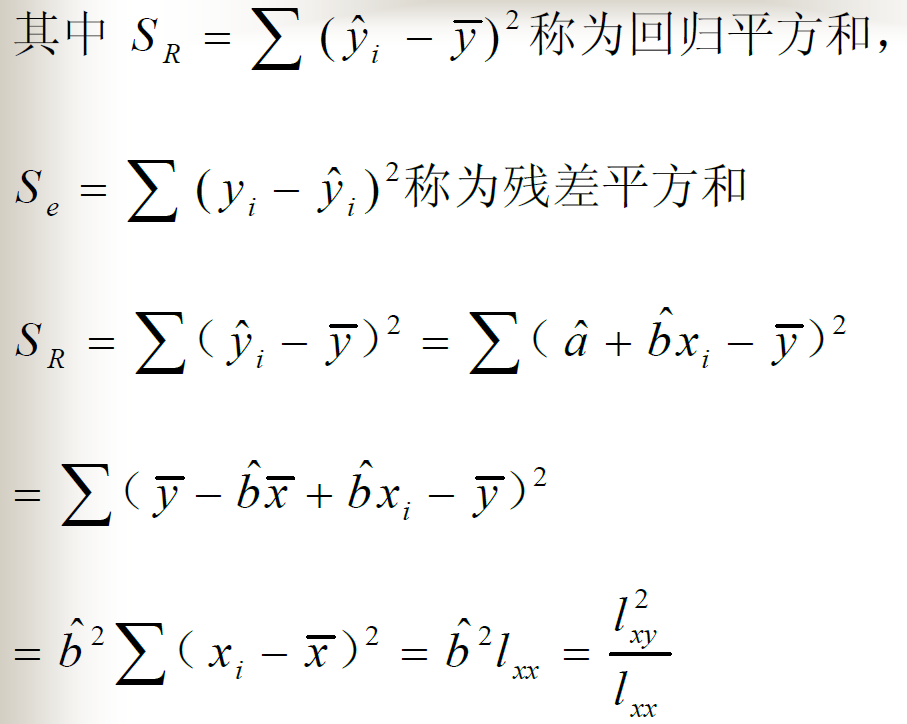

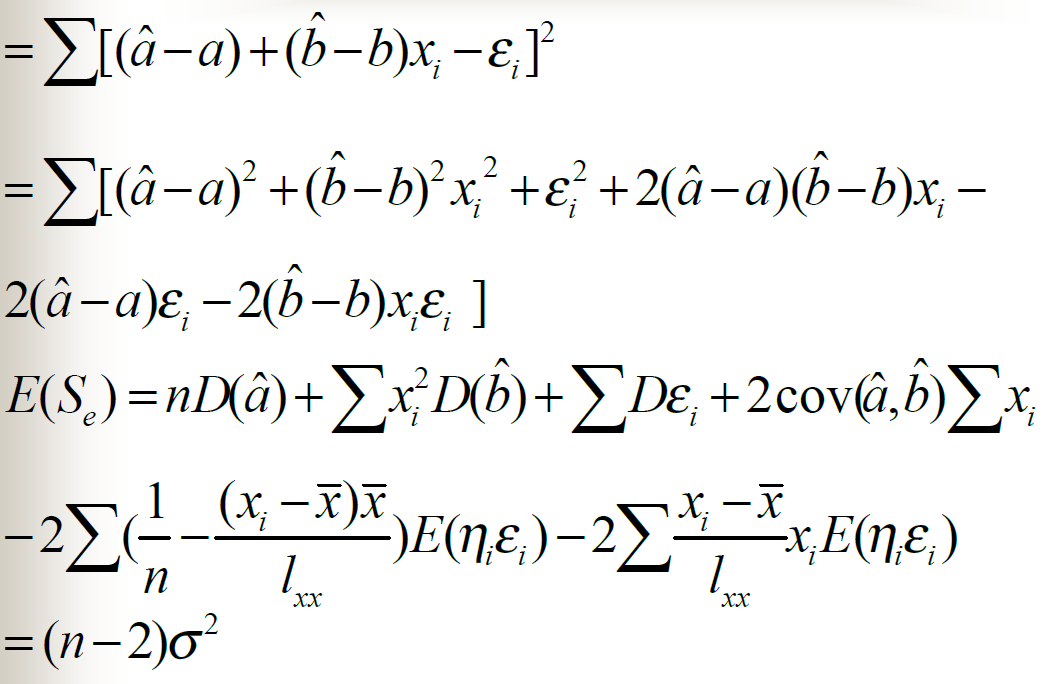


F检验法


t检验法


未知参数a,b和方差的区间估计

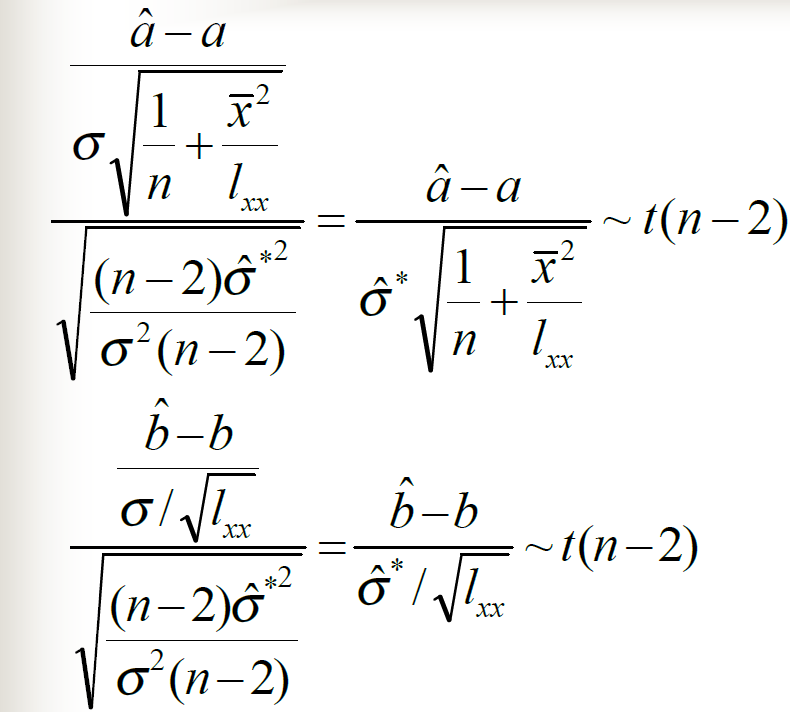

例题
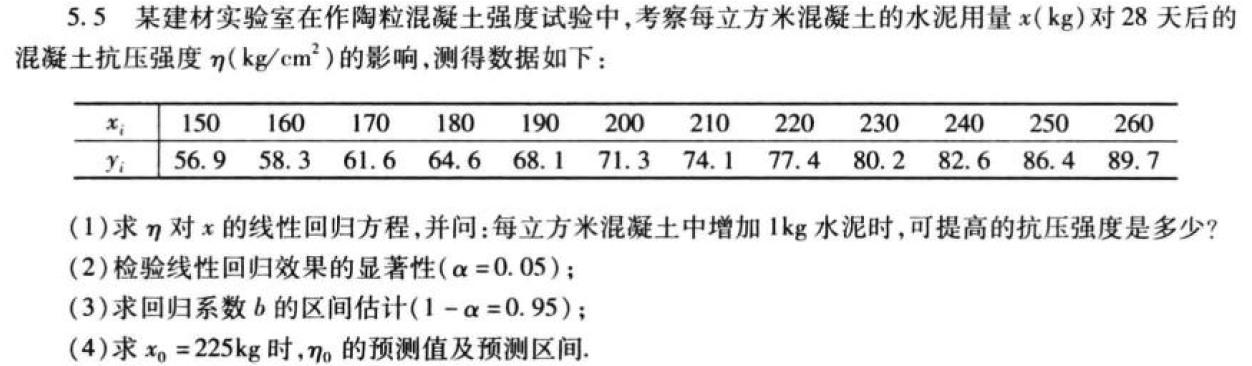
要解答这道数理统计题目,我们需要进行线性回归分析。具体步骤如下:
A. 求
给定数据:
- 计算
- 计算
- 计算回归系数
B. 检验线性回归效果的显著性 (
- 计算回归平方和
- 计算均方误差
- 利用 F 检验:
查表得到临界值
C. 求回归系数
- 计算标准误差
- 利用 t 分布确定区间:
D. 求
- 预测值
- 预测区间:
方差分析
单因子模型


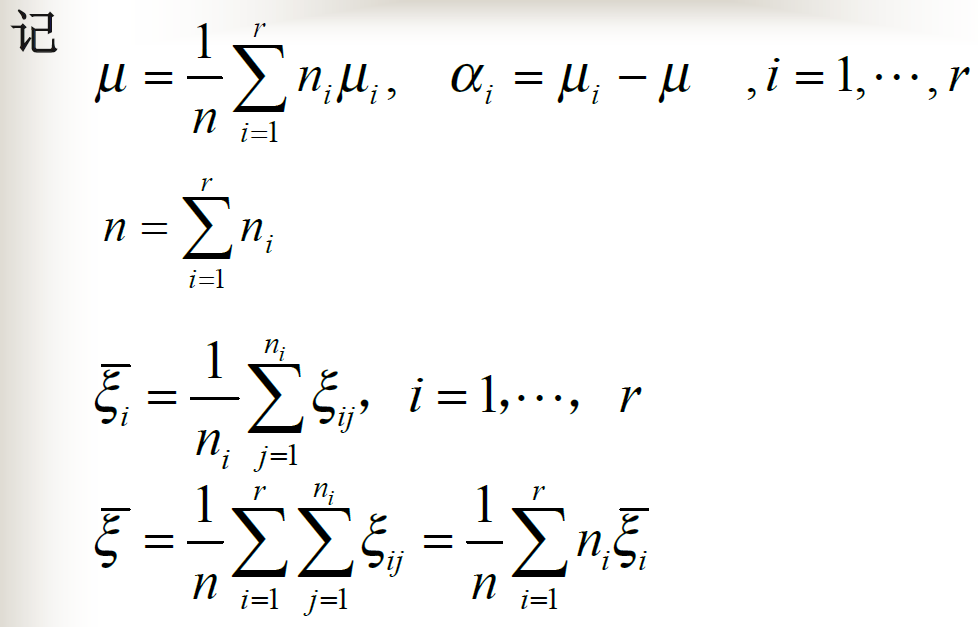



显著性检验

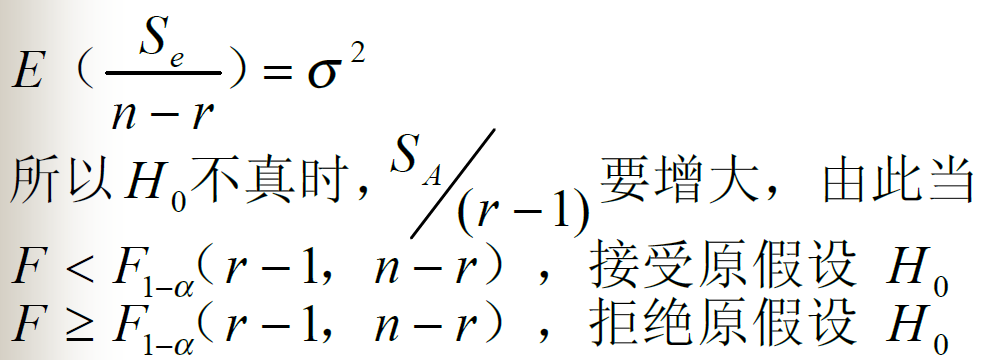
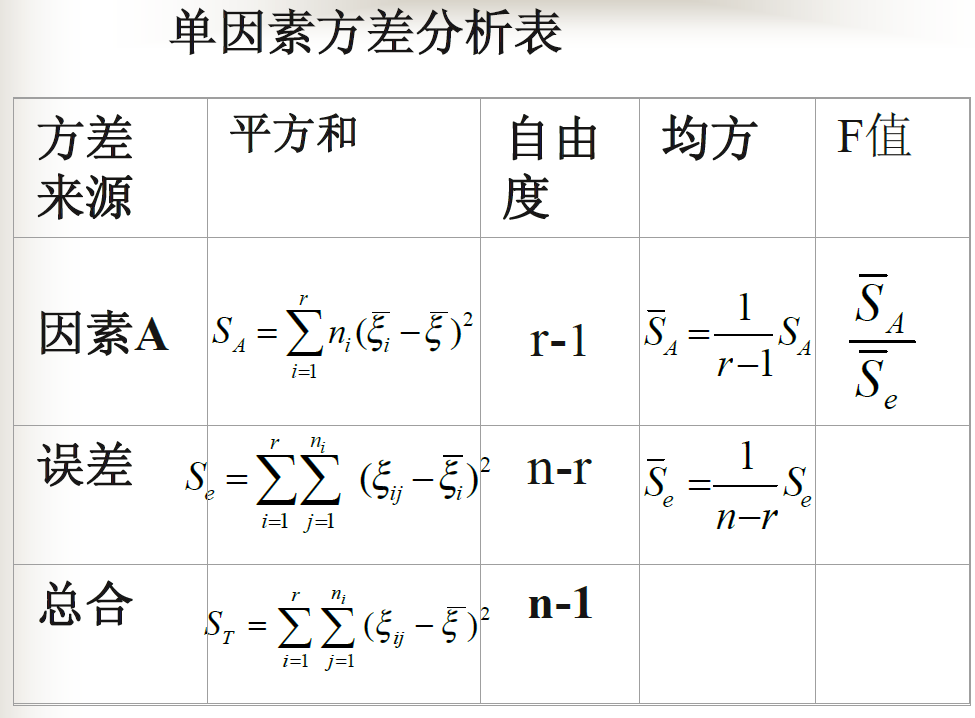
参数的估计

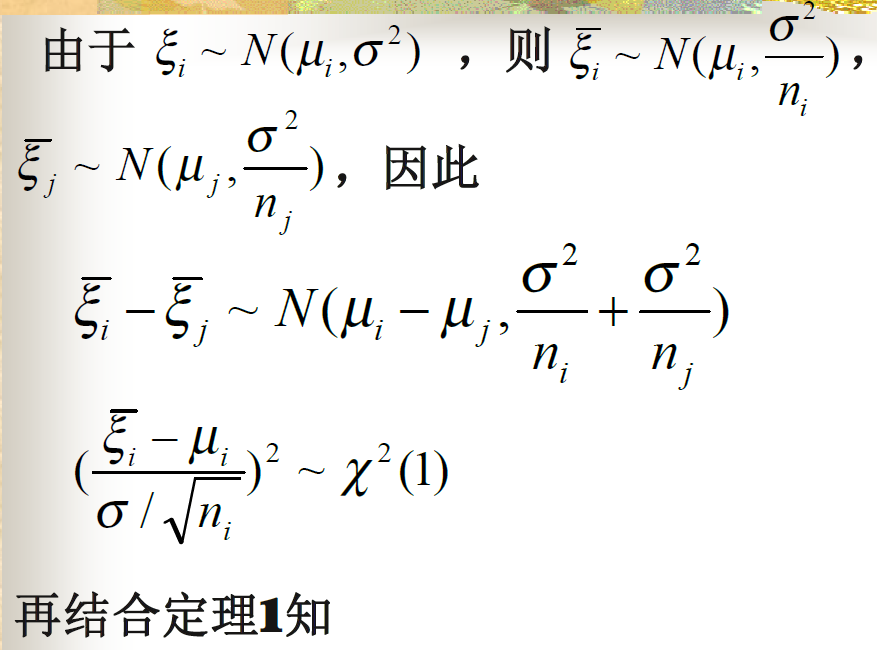
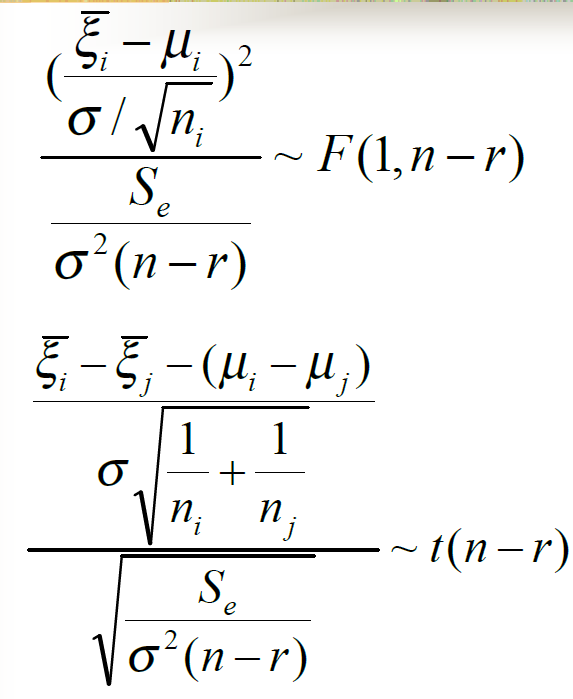


多重比较

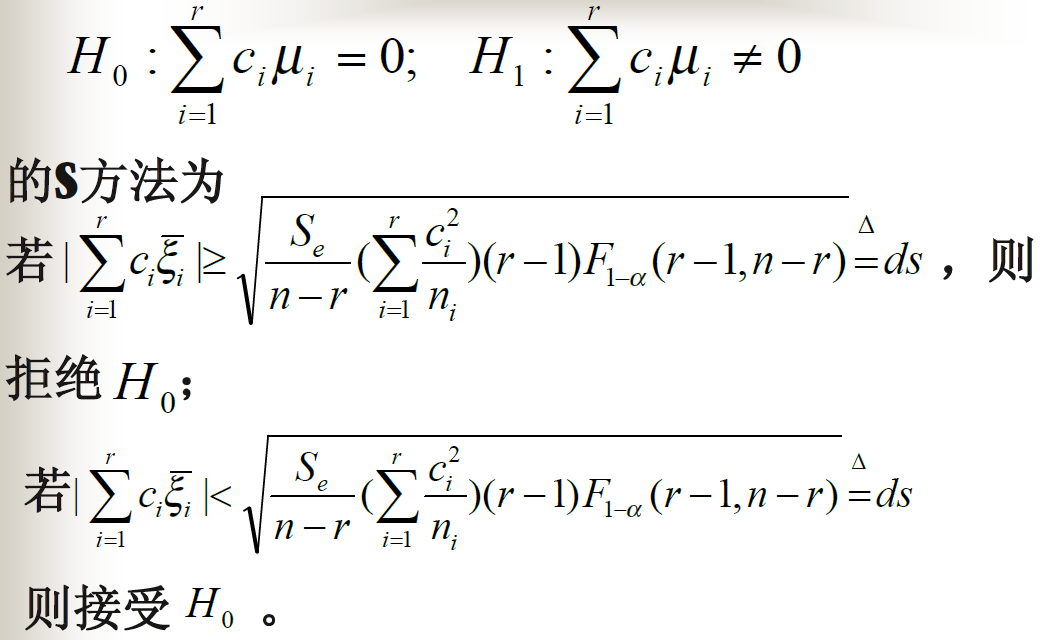

齐次性检验

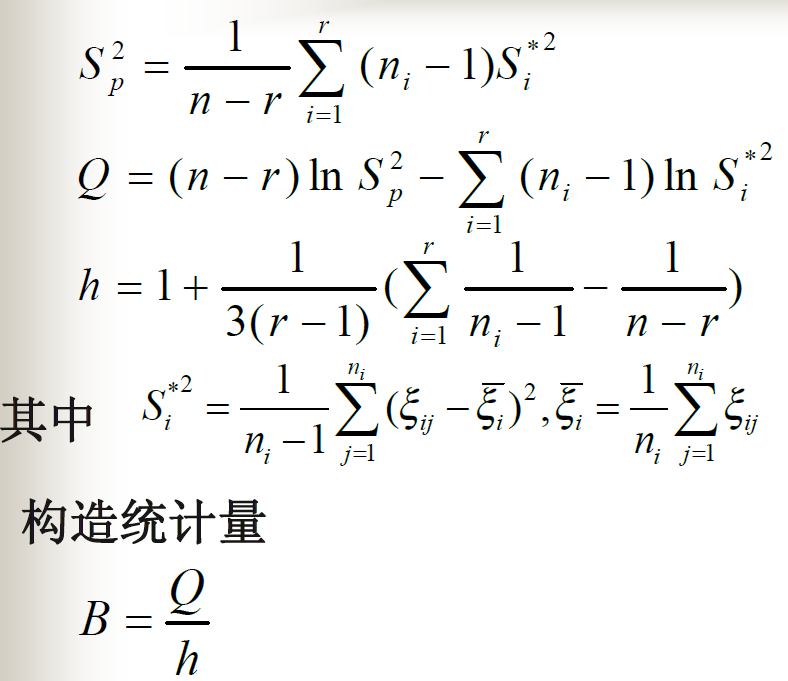

两个因素的方差分析
有交互作用的方差分析模型





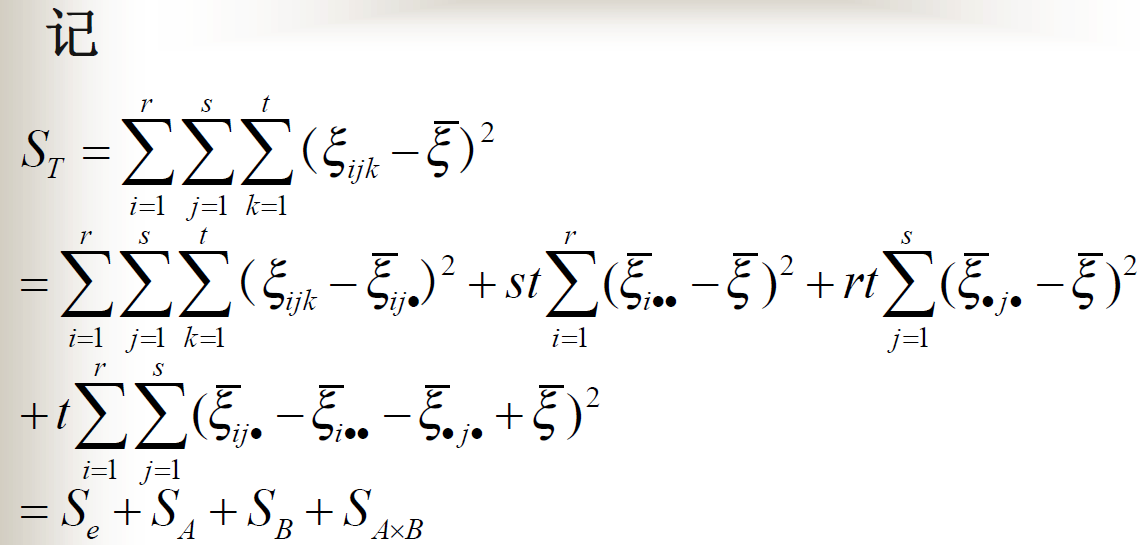
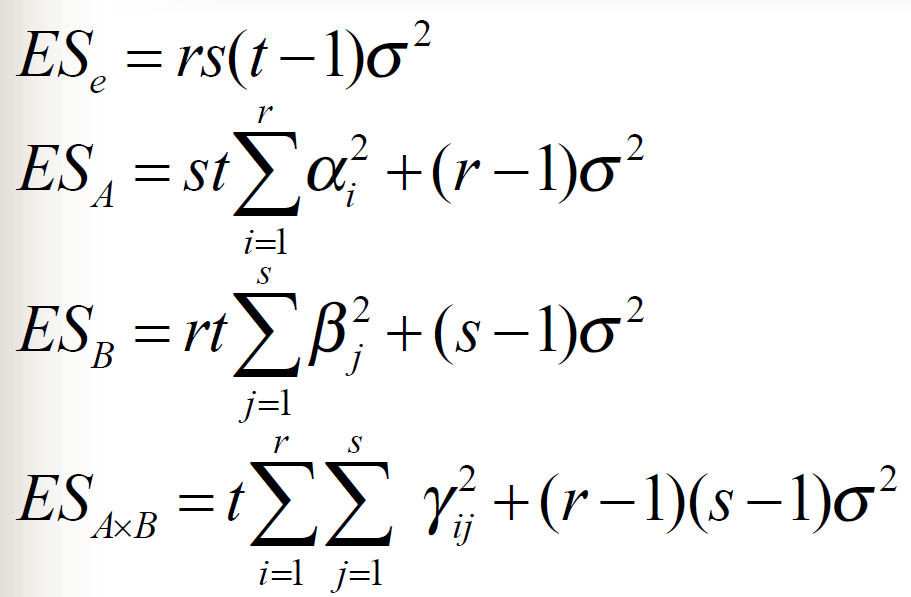
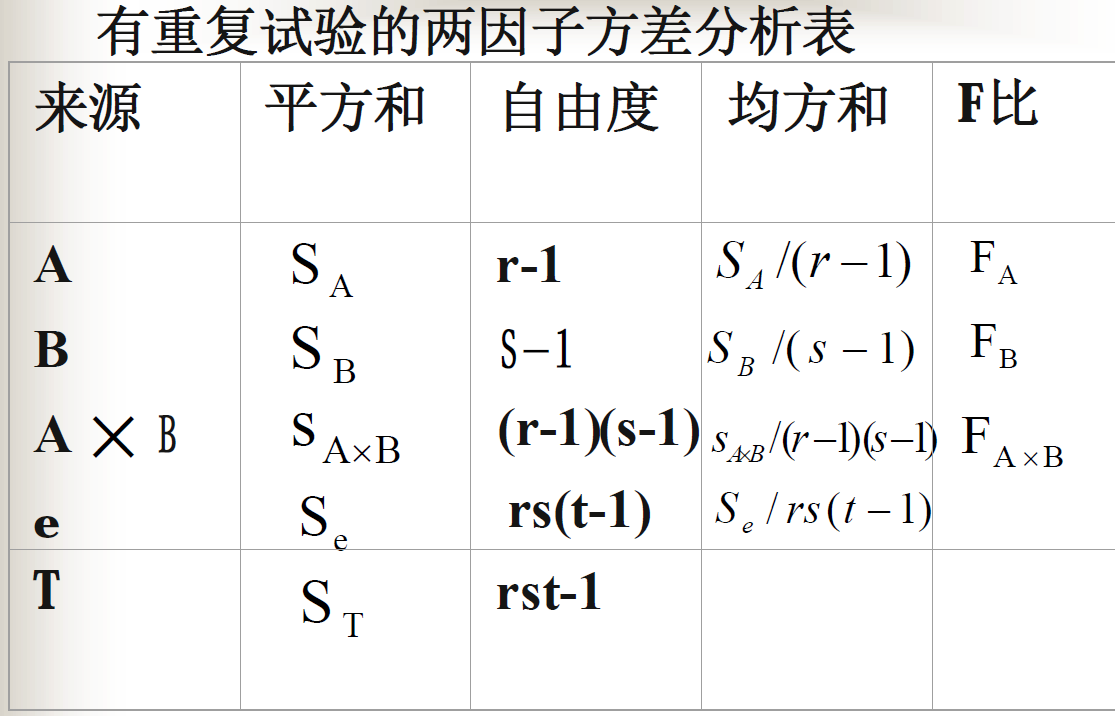

无交互作用无重复试验的方差分析模型

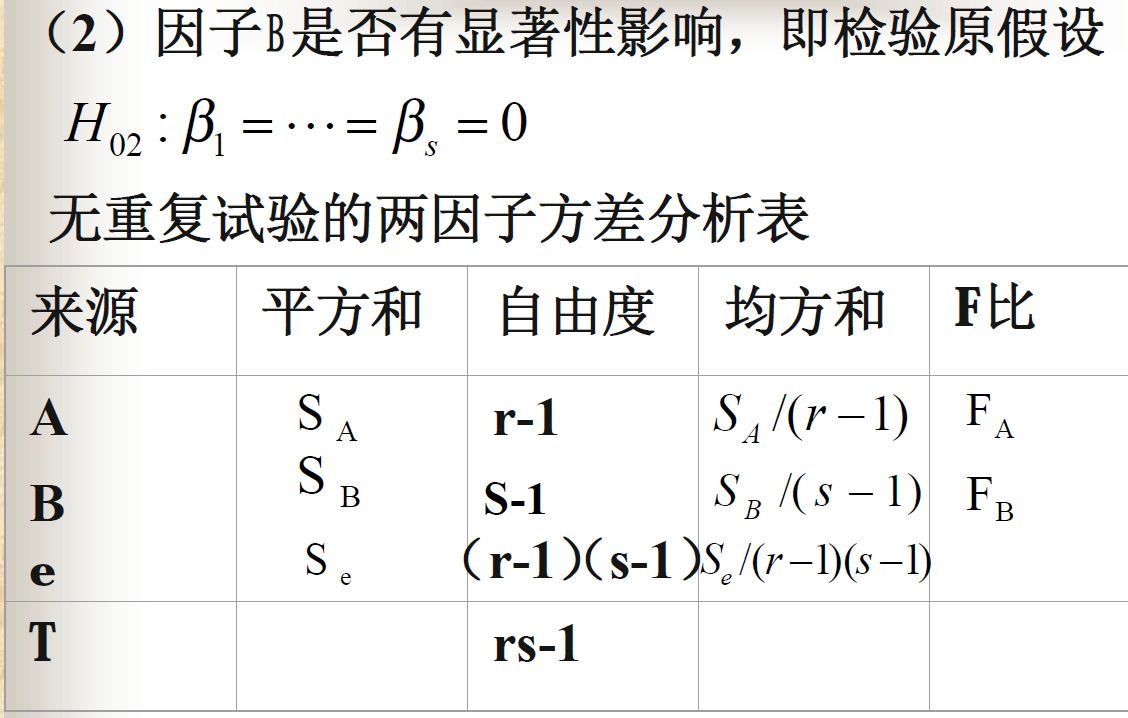
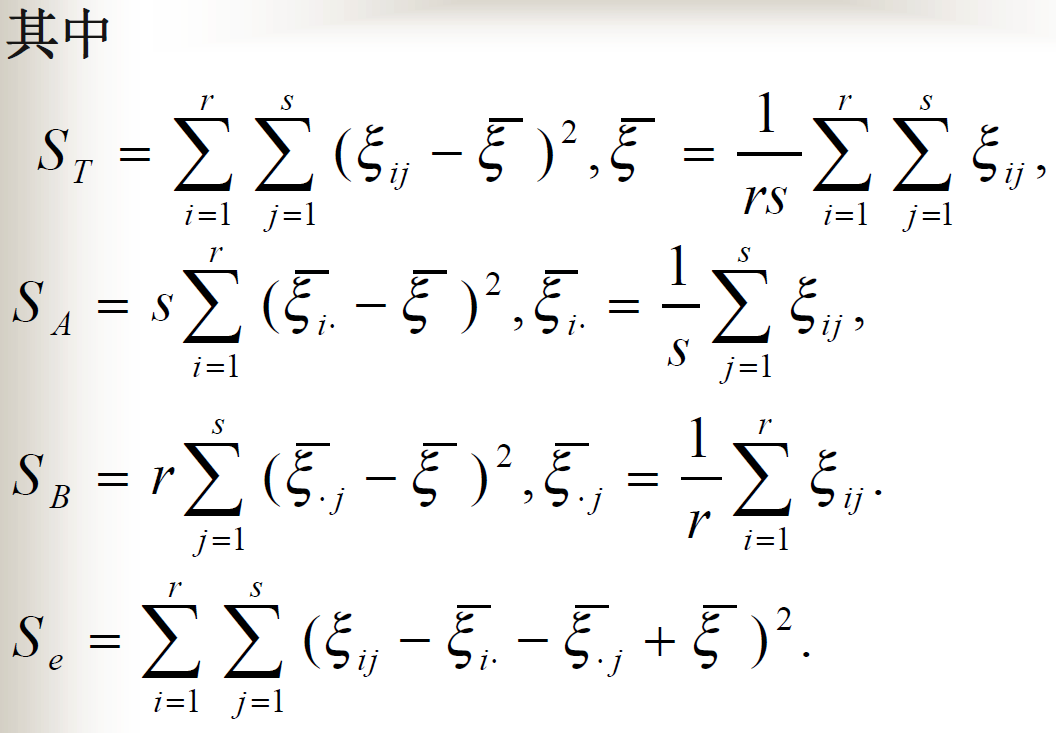

附录
正态分布的积分表
卡方分布表



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律