球体表面随机均匀采样方法shell程序（awk）

要在单位球面上随机选取一个点，从 [-180,180) 中的均匀分布经度和 [-90,90] 中均匀分布的纬度中随机选择经纬度是不正确的，因为赤道和两极的格点面积元并不相同，因此以这种方式选取的点将在极点附近“聚集”。（图片引自 https://mathworld.wolfram.com/SpherePointPicking.html ）

 

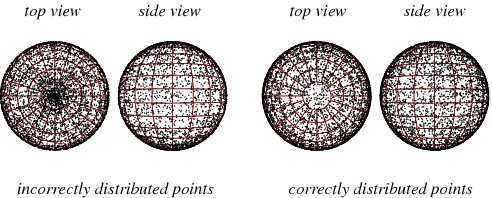
 一个简单的均匀采样方法是：三维笛卡尔坐标系中生成随机点，并投影到球面上，这样生成的点才会均匀。即生成三个高斯随机变量，x, y,和z，那么以下变量在三维球面上均匀分布的（Muller 1959, Marsaglia 1972）：

 

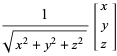
在shell脚本中写一个awk函数即可实现，以下代码实现随机选取两个点，输出它们的经纬度和大圆弧距离，输出五列单位均为度。

 1 seed=10000
 2 sum=$(echo $seed*36/3.1416/3.1416 | bc)
 3 awk 'BEGIN{srand();
 4     for ( i=0; i<='"$sum"'; i++ ){
 5         xa=2*rand()-1;
 6         ya=2*rand()-1;
 7         za=2*rand()-1;
 8         xb=2*rand()-1;
 9         yb=2*rand()-1;
10         zb=2*rand()-1;
11         norma=sqrt(xa*xa+ya*ya+za*za)
12         normb=sqrt(xb*xb+yb*yb+zb*zb)
13         if (norma<0.00001 || normb<0.00001) continue
14         if (xa*xa+ya*ya+za*za<1.0 && xb*xb+yb*yb+zb*zb<1.0){
15             xa=xa/norma
16             ya=ya/norma
17             za=za/norma
18             xb=xb/normb
19             yb=yb/normb
20             zb=zb/normb
21             dis=sqrt((xb-xa)^2+(yb-ya)^2+(zb-za)^2)
22             lona=atan2(ya,xa)/0.017453
23             lonb=atan2(yb,xb)/0.017453
24             lata=90-atan2(sqrt(xa*xa+ya*ya),za)/0.017453
25             latb=90-atan2(sqrt(xb*xb+yb*yb),zb)/0.017453
26             arc=2*atan2(dis/2,sqrt(1-dis*dis/4))/0.017453
27             printf("%8.2f %7.2f %8.2f %7.2f %8.3f\n",
28                 lona,lata,lonb,latb,arc)
29         }
30     }
31 }' > sphere_random_point.txt

备注：

seed代表最终生成文件大致行数

norma代表A点到球心距离

normb代表B点到球心距离

dis代表AB点之间弦长

arc代表AB点之间大圆弧长（度为单位）

 

References

Marsaglia, G. "Choosing a Point from the Surface of a Sphere." Ann. Math. Stat. 43, 645-646, 1972.

Muller, M. E. "A Note on a Method for Generating Points Uniformly on N-Dimensional Spheres." Comm. Assoc. Comput. Mach. 2, 19-20, Apr. 1959.

 

 
 

，弧

noun: 弧, 弧形, 弧光

posted @ 2021-12-29 09:52  Philbert  阅读(875)  评论(0)  编辑  收藏  举报