python中的函数递归和迭代问题
一、递归
1、递归的介绍
- 什么是递归?
程序调用自身的编程技巧称为递归( recursion)。递归做为一种算法在程序设计语言中广泛应用。 一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解,递归策略只需少量的程序就可描述出解题过程所需要的多次重复计算,大大地减少了程序的代码量。递归的能力在于用有限的语句来定义对象的无限集合。一般来说,递归需要有边界条件、递归前进段和递归返回段。当边界条件不满足时,递归前进;当边界条件满足时,递归返回。
递归要注意的是,它是直接或间接调用自身,所以在使用递归时,必须有一个明确的递归结束条件,称为递归出口,否则,他就会陷入死循环。
- 尾递归
具体可以看一下博客https://blog.csdn.net/ialexanderi/article/details/81482878
如果一个函数中所有递归形式的调用都出现在函数的末尾,我们称这个递归函数是尾递归的。当递归调用是整个函数体中最后执行的语句且它的返回值不属于表达式的一部分时,这个递归调用就是尾递归。尾递归函数的特点是在回归过程中不用做任何操作,这个特性很重要,因为大多数现代的编译器会利用这种特点自动生成优化的代码。
- python不是一门函数式编程语言,本身不支持尾递归(没有对尾递归做优化),而且对递归的次数有限制,当递归深度超过1000时,会抛出异常,虽然可以通过sys模块修改提柜的深度,,但是因为不是尾递归,仍然要保存栈,内存大小一定,不可能无限递归,而且无限制地递归调用本身是毫无意义的
import sys sys.getrecursionlimit() sys.setrecursionlimit(2000) # 修改递归深度为2000
关于递归的优化可以参考这篇文章:http://www.cnblogs.com/Alexander-Lee/archive/2010/09/16/1827587.html
2、递归的应用
- 递归分为两个阶段:回溯和递推
-
递推 : 把复杂的问题的求解推到比原问题简单一些的问题的求解;
-
回溯 : 当获得最简单的情况(递归出口)后,逐步返回,依次得到复杂的解
下面通过一个例子来分析这个过程 :
这是一个十进制转化为二进制的函数,十进制转化为二进制就是 将十进制不断地除以2,直到商为0,然后将余数从后到前排列起来
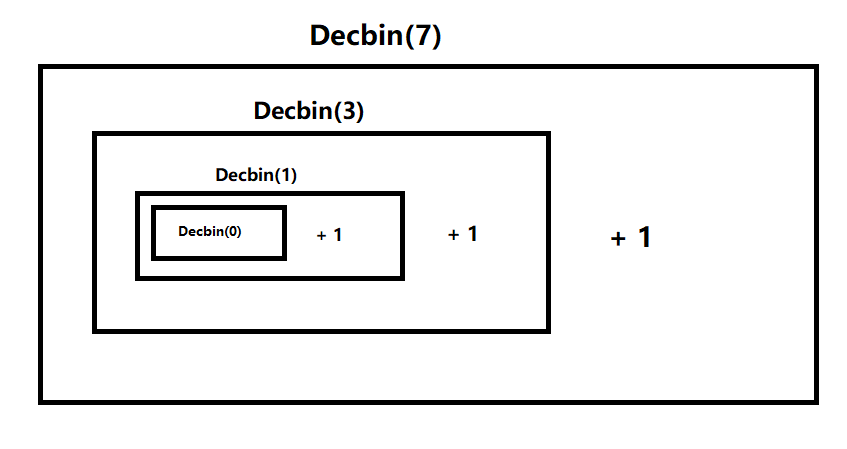
def Decbin(x): result = '' if x: return Decbin(x // 2) + str(x % 2) else: return result print(Decbin(7))
当我们传入x为7时,很明显x不为0,所以我们便进入了下次一循环,注意这时的第一层函数并没有结束,而是一直在等待着下一层函数的返回结果。接着进入了第二层函数,参数为3,很明显也不为0,接着又进入了第三层函数,此时第二层函数也在等待下一层函数的返回结果,以此类推,这就是递归函数的回溯。当我们的参数为0的时候,便会执行else的代码,这时候函数就不再回溯,而是开始往前递推。
二、迭代与递归
1、什么是迭代?
Python中的迭代是指通过重复执行的代码处理相似的数据集的过程,并且本次迭代的处理数据要依赖上一次的结果继续往下做,上一次产生的结果为下一次产生结果的初始状态,如果中途有任何停顿,都不能算是迭代。常见的for循环遍历对象就是迭代。
2、用python实现递归算法,代码结构较为简单,但效率非常低下,而迭代算法可读性强,执行效率也非常之快。所以在运用递归算法时应谨慎,具体可以看一下博客https://blog.csdn.net/wuu1299/article/details/78951328


