《挑战程序设计竞赛》2.1 深度优先搜索 POJ2386 POJ1979 AOJ0118 AOJ0033 POJ3009
POJ2386
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 25366 | Accepted: 12778 |
Description
Given a diagram of Farmer John's field, determine how many ponds he has.
Input
* Lines 2..N+1: M characters per line representing one row of Farmer John's field. Each character is either 'W' or '.'. The characters do not have spaces between them.
Output
Sample Input
10 12 W........WW. .WWW.....WWW ....WW...WW. .........WW. .........W.. ..W......W.. .W.W.....WW. W.W.W.....W. .W.W......W. ..W.......W.
Sample Output
3
Hint
There are three ponds: one in the upper left, one in the lower left,and one along the right side.
Source
思路:
园子里下了雨有积水,八连通的积水被认为是连接在一起的。求园子里有多少水洼。
确实是比较经典的深搜。
代码:
Source Code
Problem: 2386 User: liangrx06
Memory: 1320K Time: 16MS
Language: G++ Result: Accepted
Source Code
#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
#define N 100
int n, m;
char lake[N][N+1];
void input()
{
cin >> n >> m;
for (int i=0; i<n; i++) {
cin >> lake[i];
}
}
void dfs(int x, int y)
{
lake[x][y] = '.';
for (int dx=-1; dx<=1; dx++) {
for (int dy=-1; dy<=1; dy++) {
if (!dx && !dy)
continue;
int nx = x + dx, ny = y + dy;
if (0 <= nx && nx < n && 0 <= ny && ny < m
&& lake[nx][ny] == 'W')
dfs(nx, ny);
}
}
}
void solve() {
int res = 0;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (lake[i][j] == 'W') {
dfs(i, j);
res ++;
}
}
}
printf("%d\n", res);
}
int main(void)
{
input();
solve();
return 0;
}
POJ1979
| Time Limit: 1000MS | Memory Limit: 30000K | |
| Total Submissions: 27075 | Accepted: 14714 |
Description
Write a program to count the number of black tiles which he can reach by repeating the moves described above.
Input
There are H more lines in the data set, each of which includes W characters. Each character represents the color of a tile as follows.
'.' - a black tile
'#' - a red tile
'@' - a man on a black tile(appears exactly once in a data set)
The end of the input is indicated by a line consisting of two zeros.
Output
Sample Input
6 9 ....#. .....# ...... ...... ...... ...... ...... #@...# .#..#. 11 9 .#......... .#.#######. .#.#.....#. .#.#.###.#. .#.#..@#.#. .#.#####.#. .#.......#. .#########. ........... 11 6 ..#..#..#.. ..#..#..#.. ..#..#..### ..#..#..#@. ..#..#..#.. ..#..#..#.. 7 7 ..#.#.. ..#.#.. ###.### ...@... ###.### ..#.#.. ..#.#.. 0 0
Sample Output
45 59 6 13
Source
思路:
人的初始位置是@,点代表黑色地板可以走,#代表白色不能走,每次只可以上下左右走一步。问能到达多少黑色地板。
深搜即可。
代码:
Source Code
Problem: 1979 User: liangrx06
Memory: 212K Time: 0MS
Language: C++ Result: Accepted
Source Code
#include <iostream>
#include <cstdio>
using namespace std;
#define N 20
int n, m;
char tile[N][N+1];
int number;
void dfs(int x, int y)
{
tile[x][y] = '#';
int d[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int i = 0; i < 4; i ++) {
int nx = x + d[i][0], ny = y + d[i][1];
if (0 <= nx && nx < n && 0 <= ny && ny < m
&& tile[nx][ny] == '.') {
number ++;
dfs(nx, ny);
}
}
}
void solve() {
char *c;
int bx, by;
for (int i=0; i<n; i++) {
if ( c = strstr(tile[i], "@") ) {
bx = i;
by = c - tile[i];
}
}
number = 1;
dfs(bx, by);
printf("%d\n", number);
}
int main(void)
{
while (cin >> m >> n) {
if (!m && !n)
break;
for (int i=0; i<n; i++) {
cin >> tile[i];
}
solve();
}
return 0;
}AOJ0118
| Time Limit: 1000MS | Memory Limit: 65536KB | 64bit IO Format: %lld & %llu |
Description
タナカ氏が HW アールの果樹園を残して亡くなりました。果樹園は東西南北方向に H×W の区画に分けられ、区画ごとにリンゴ、カキ、ミカンが植えられています。タナカ氏はこんな遺言を残していました。
果樹園は区画単位でできるだけ多くの血縁者に分けること。ただし、ある区画の東西南北どれかの方向にとなりあう区画に同じ種類の果物が植えられていた場合は、区画の境界が分からないのでそれらは 1 つの大きな区画として扱うこと。
例えば次のような 3x10 の区画であれば(リはリンゴ、カはカキ、ミはミカンを表す)
同じ樹がある区画の間の境界を消すと次のようになり、
結局 10 個の区画、つまり 10 人で分けられることになります。 雪が降って区画の境界が見えなくなる前に分配を終えなくてはなりません。あなたの仕事は果樹園の地図を もとに分配する区画の数を決めることです。ということで、果樹園の地図を読み込み、分配を受けら れる血縁者の人数を出力して終了するプログラムを作成してください。ただし、果樹園の地図は W 文字×H 行の文字列として与えられます。この文字列には、リンゴを表す@、カキを表す#、ミカンを表す*、の 3 文字しか使われていません。
Input
複数のデータセットが与えられます。各データセットは空白で区切られたH Wを含む行から始まり、続いてH × Wの文字が与えられます。入力はゼロが2つの行で終わります。
H, W は100以下です。
Output
各データセットごとに、分配を受ける人数を1行に出力してください。
Sample Input
10 10 ####*****@ @#@@@@#*#* @##***@@@* #****#*@** ##@*#@@*## *@@@@*@@@# ***#@*@##* *@@@*@@##@ *@*#*@##** @****#@@#@ 0 0
Output for the Sample Input
33
Source
(extended version)
http://www.pref.fukushima.jp/pc-concours/
思路:
原题是日文版的,中文题意是:
在H * W的矩形果园里有苹果、梨、蜜柑三种果树, 相邻(上下左右)的同种果树属于同一个区域,给出果园的果树分布,求总共有多少个区域。 (原题的样图中苹果为リ,梨为カ,蜜柑为ミ, 图中共10个区域)
输入:
多组数据,每组数据第一行为两个整数H,W(H <= 100, W <= 100), H =0 且 W = 0代表输入结束。以下H行W列表示果园的果树分布, 苹果是@,梨是#, 蜜柑是*。
输出:
对于每组数据,输出其区域的个数。
解题思路是对未搜索过的每个点进行神搜,搜索过的位置置为‘X’,在最上层函数中进行计数。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
#define N 100
int n, m;
char tile[N][N+1];
int number;
void dfs(int x, int y, char c)
{
tile[x][y] = 'X';
int d[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int i = 0; i < 4; i ++) {
int nx = x + d[i][0], ny = y + d[i][1];
if (0 <= nx && nx < n && 0 <= ny && ny < m
&& tile[nx][ny] == c) {
dfs(nx, ny, c);
}
}
}
void solve() {
int res = 0;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (tile[i][j] != 'X') {
dfs(i, j, tile[i][j]);
res ++;
}
}
}
printf("%d\n", res);
}
int main(void)
{
while (cin >> n >> m) {
if (!m && !n)
break;
for (int i=0; i<n; i++) {
cin >> tile[i];
}
solve();
}
return 0;
}
AOJ0033
| Time Limit: 1000MS | Memory Limit: 65536KB | 64bit IO Format: %lld & %llu |
Description
図のように二股に分かれている容器があります。1 から10 までの番号が付けられた10 個の玉を容器の開口部 A から落とし、左の筒 B か右の筒 C に玉を入れます。板 D は支点 E を中心に左右に回転できるので、板 D を動かすことで筒 B と筒 C のどちらに入れるか決めることができます。開口部 A から落とす玉の並びを与えます。それらを順番に筒 B 又は筒 Cに入れていきます。このとき、筒 B と筒 C のおのおのが両方とも番号の小さい玉の上に大きい玉を並べられる場合は YES、並べられない場合は NO と半角大文字で出力して終了するプログラムを作成してください。ただし、容器の中で玉の順序を入れ替えることはできないものとします。また、続けて同じ筒に入れることができるものとし、筒 B, C ともに10 個の玉がすべて入るだけの余裕があるとします。
Input
複数のデータセットが与えられます。1行目にデータセット数 N が与えられます。つづいて、N 行のデータセットが与えられます。各データセットに 10 個の番号が与えられます。左から1番目の玉の番号、2番目の玉の番号、、、といった順番です。
Output
各データセットに対して、YES または NO を出力して下さい。
Sample Input
2 3 1 4 2 5 6 7 8 9 10 10 9 8 7 6 5 4 3 2 1
Output for the Sample Input
YES NO
Source
http://www.pref.fukushima.jp/pc-concours/
思路:
有一个形似央视大楼的筒,从A口可以放球,放进去的球可通过挡板DE使其掉进B管或C管里,现有带1-10标号的球按给定顺序从A口放入,问是否有一种控制挡板的策略可以使B管和C管中的球从下往上标号递增。
输入:第一行输入数据组数N。接下来N行为N组具体数据,每组数据中有10个整数,代表球的放入顺序。
输出:
对于每组数据,若策略存在,输出YES;若不存在,输出NO。
用穷举或者DFS搜索都可以。我这里用了代码相对简单的枚举。位运算能够降低存储。
代码:
#include <iostream>
#include <cstdio>
using namespace std;
const int N = 10;
int a[N];
void input()
{
for (int i = 0; i < N; i ++) {
scanf("%d", &a[i]);
}
}
void solve()
{
bool res = false;
for (int k = 0; k < (1<<10); k++) {
int num = 0;
int i;
for (i = 0; i < N; i ++) {
if ( (1 << i)&k ) {
if (a[i] > num)
num = a[i];
else
break;
}
}
if (i < N)
continue;
num = 0;
for (i = 0; i < N; i ++) {
if ( ((1 << i)&k) == 0 ) {
if (a[i] > num)
num = a[i];
else
break;
}
}
if (i == N) {
res = true;
//printf("k=%d\n", k);
break;
}
}
if (res)
printf("YES\n");
else
printf("NO\n");
}
int main(void)
{
int t;
cin >> t;
while (t--) {
input();
solve();
}
return 0;
}
POJ3009
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 15450 | Accepted: 6390 |
Description
On Planet MM-21, after their Olympic games this year, curling is getting popular. But the rules are somewhat different from ours. The game is played on an ice game board on which a square mesh is marked. They use only a single stone. The purpose of the game is to lead the stone from the start to the goal with the minimum number of moves.
Fig. 1 shows an example of a game board. Some squares may be occupied with blocks. There are two special squares namely the start and the goal, which are not occupied with blocks. (These two squares are distinct.) Once the stone begins to move, it will proceed until it hits a block. In order to bring the stone to the goal, you may have to stop the stone by hitting it against a block, and throw again.

Fig. 1: Example of board (S: start, G: goal)
The movement of the stone obeys the following rules:
- At the beginning, the stone stands still at the start square.
- The movements of the stone are restricted to x and y directions. Diagonal moves are prohibited.
- When the stone stands still, you can make it moving by throwing it. You may throw it to any direction unless it is blocked immediately(Fig. 2(a)).
- Once thrown, the stone keeps moving to the same direction until one of the following occurs:
- The stone hits a block (Fig. 2(b), (c)).
- The stone stops at the square next to the block it hit.
- The block disappears.
- The stone gets out of the board.
- The game ends in failure.
- The stone reaches the goal square.
- The stone stops there and the game ends in success.
- The stone hits a block (Fig. 2(b), (c)).
- You cannot throw the stone more than 10 times in a game. If the stone does not reach the goal in 10 moves, the game ends in failure.
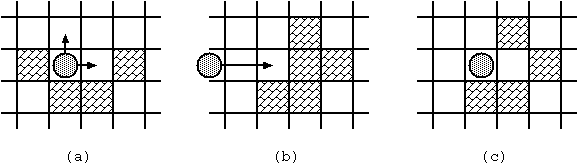
Fig. 2: Stone movements
Under the rules, we would like to know whether the stone at the start can reach the goal and, if yes, the minimum number of moves required.
With the initial configuration shown in Fig. 1, 4 moves are required to bring the stone from the start to the goal. The route is shown in Fig. 3(a). Notice when the stone reaches the goal, the board configuration has changed as in Fig. 3(b).
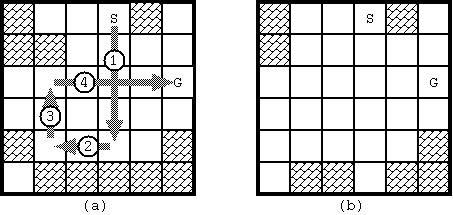
Fig. 3: The solution for Fig. D-1 and the final board configuration
Input
The input is a sequence of datasets. The end of the input is indicated by a line containing two zeros separated by a space. The number of datasets never exceeds 100.
Each dataset is formatted as follows.
the width(=w) and the height(=h) of the board
First row of the board
...
h-th row of the board
The width and the height of the board satisfy: 2 <= w <= 20, 1 <= h <= 20.
Each line consists of w decimal numbers delimited by a space. The number describes the status of the corresponding square.
0 vacant square 1 block 2 start position 3 goal position
The dataset for Fig. D-1 is as follows:
6 6
1 0 0 2 1 0
1 1 0 0 0 0
0 0 0 0 0 3
0 0 0 0 0 0
1 0 0 0 0 1
0 1 1 1 1 1
Output
For each dataset, print a line having a decimal integer indicating the minimum number of moves along a route from the start to the goal. If there are no such routes, print -1 instead. Each line should not have any character other than this number.
Sample Input
2 1 3 2 6 6 1 0 0 2 1 0 1 1 0 0 0 0 0 0 0 0 0 3 0 0 0 0 0 0 1 0 0 0 0 1 0 1 1 1 1 1 6 1 1 1 2 1 1 3 6 1 1 0 2 1 1 3 12 1 2 0 1 1 1 1 1 1 1 1 1 3 13 1 2 0 1 1 1 1 1 1 1 1 1 1 3 0 0
Sample Output
1 4 -1 4 10 -1
Source
思路:
题意是:已知起点和终点,求石子从起点到达终点的最短路,如果无法到达,则输出-1。
石子移动的具体规则如下:
1、开始时,石子在起点s处
2、运动方向可以是水平或垂直的,不能斜方向运动
3、最开始的时候,你可以将石子向上下左右任意一个方向抛,如果与它相邻的点是障碍物的话除外
4、一旦石子开始运动,有三种可能:
a、遇到障碍物,石子会停在障碍物的前一格,障碍物会消失
b、如果出界,游戏失败
c、到达终点,游戏结束并成功
5、如果移动的次数超过10次,将认为游戏是失败的
图中各方格的标示为:
0代表无障碍;
1有障碍;
2为起点;
3为终点。
需要注意的几个地方:
1、石子碰到障碍物时障碍物会消失。也就是说每走一步图的状态都会发生改变,这导致BFS无法成功。
2、移动次数10次实际上是帮助剪枝的,最小步数也可帮助剪枝。
解法:
所以比较合适的解法是DFS,DFS前要对障碍物1更新为0,结束后更改回来。即此题的解法为DFS+回溯。
代码:
Source Code
Problem: 3009 User: liangrx06
Memory: 236K Time: 32MS
Language: C++ Result: Accepted
Source Code
#include <iostream>
#include <cstdio>
using namespace std;
#define N 20
#define MAX_STEP 10
int n, m;
int map[N][N];
int minStep;
bool legal(int x, int y)
{
return 0 <= x && x < n && 0 <= y && y < m;
}
void dfs(int x, int y, int step)
{
if (step >= MAX_STEP || step >= minStep)
return;
int d[4][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
for (int i = 0; i < 4; i ++) {
int nx = x + d[i][0], ny = y + d[i][1];
if (!legal(nx, ny) || map[nx][ny] == 1)
continue;
if (map[nx][ny] == 3) {
minStep = step + 1;
continue;
}
while (true) {
nx += d[i][0], ny += d[i][1];
if (!legal(nx, ny))
break;
else if (map[nx][ny] == 1) {
map[nx][ny] = 0;
dfs(nx-d[i][0], ny-d[i][1], step+1);
map[nx][ny] = 1;
break;
}
else if (map[nx][ny] == 3) {
minStep = step + 1;
break;
}
}
}
}
void solve() {
int bx, by;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
if (map[i][j] == 2) {
bx = i; by = j;
}
}
}
minStep = MAX_STEP + 1;
dfs(bx, by, 0);
if (minStep <= MAX_STEP)
printf("%d\n", minStep);
else
printf("%d\n", -1);
}
int main(void)
{
while (cin >> m >> n) {
if (!m && !n)
break;
for (int i=0; i<n; i++) {
for (int j=0; j<m; j++) {
scanf("%d", &map[i][j]);
}
}
solve();
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号