《挑战程序设计竞赛》2.1 广度优先搜索 AOJ0558 POJ3669 AOJ0121
AOJ0558
原文链接:
题意:
在H * W的地图上有N个奶酪工厂,分别生产硬度为1-N的奶酪。有一只吃货老鼠准备从老鼠洞出发吃遍每一个工厂的奶酪。老鼠有一个体力值,初始时为1,每吃一个工厂的奶酪体力值增加1(每个工厂只能吃一次),且老鼠只能吃硬度不大于当前体力值的奶酪。
老鼠从当前格走到相邻的无障碍物的格(上下左右)需要时间1单位,有障碍物的格不能走。走到工厂上时即可吃到该工厂的奶酪,吃奶酪时间不计。问吃遍所有奶酪最少用时。
输入:第一行三个整数H(1 <= H <= 1000)、W(1 <= W <=1000)、N(1 <= N <= 9),之后H行W列为地图, “.“为空地, ”X“为障碍物,”S“为老鼠洞, 1-N代表硬度为1-N的奶酪的工厂。
思路:
按照题意,当老鼠的体力值为k时,她下一个只能去吃硬度为k的奶酪。其实这个题就是从S开始,再到1,到2,最后到N,找最短路径。
此类题用最短路径算法当然是不合适的,会TLE。最适合的算法是BFS。所以这个题的做法是做N次BFS,总的时间就是要求的结果。
需要注意的是,老鼠在走动过程中,只有有障碍物的格子不能走,其它的格子(. S 1-N)都是可以途经的,当然经过1-N时除了那个等于体力值的格子都不能吃掉奶酪。
代码:
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
using namespace std;
const int N = 1000;
const int INF = 0x3f3f3f3f;
int n, m, f;
char map[N][N+1];
bool legal(int x, int y, int k)
{
return x >= 0 && x < n && y >= 0 && y < m
&& map[x][y] != 'X';
}
void input()
{
cin >> n >> m >> f;
for (int i = 0; i < n; i ++) {
scanf("%s", map[i]);
}
}
int BFS(int k)
{
int i, j;
int d[N][N];
typedef pair<int, int> P;
queue <P> q;
for (i = 0; i < n; i ++) {
for (j = 0; j < m; j ++) {
d[i][j] = INF;
if ((k == 0 && map[i][j] == 'S') || map[i][j] == '0'+k) {
q.push(P(i, j));
d[i][j] = 0;
map[i][j] = '.';
}
}
}
while( q.size() ) {
P p = q.front();
q.pop();
int x = p.first;
int y = p.second;
if (map[x][y] == INF)
return d[x][y];
int pos[4][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
for (i = 0; i < 4; i ++) {
int nx = x + pos[i][0];
int ny = y + pos[i][1];
if (legal(nx, ny, k) && d[nx][ny] == INF) {
q.push(P(nx, ny));
d[nx][ny] = d[x][y]+1;
if (map[nx][ny] == '0'+k+1) {
return d[nx][ny];
}
}
}
}
return INF;
}
void solve()
{
int res = 0;
for (int i = 0; i < f; i ++) {
res += BFS(i);
}
printf("%d\n", res);
}
int main(void)
{
input();
solve();
return 0;
}
POJ3669
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 12472 | Accepted: 3369 |
Description
Bessie hears that an extraordinary meteor shower is coming; reports say that these meteors will crash into earth and destroy anything they hit. Anxious for her safety, she vows to find her way to a safe location (one that is never destroyed by a meteor) . She is currently grazing at the origin in the coordinate plane and wants to move to a new, safer location while avoiding being destroyed by meteors along her way.
The reports say that M meteors (1 ≤ M ≤ 50,000) will strike, with meteor i will striking point (Xi, Yi) (0 ≤ Xi ≤ 300; 0 ≤ Yi ≤ 300) at time Ti (0 ≤ Ti ≤ 1,000). Each meteor destroys the point that it strikes and also the four rectilinearly adjacent lattice points.
Bessie leaves the origin at time 0 and can travel in the first quadrant and parallel to the axes at the rate of one distance unit per second to any of the (often 4) adjacent rectilinear points that are not yet destroyed by a meteor. She cannot be located on a point at any time greater than or equal to the time it is destroyed).
Determine the minimum time it takes Bessie to get to a safe place.
Input
* Line 1: A single integer: M
* Lines 2..M+1: Line i+1 contains three space-separated integers: Xi, Yi, and Ti
Output
* Line 1: The minimum time it takes Bessie to get to a safe place or -1 if it is impossible.
Sample Input
4 0 0 2 2 1 2 1 1 2 0 3 5
Sample Output
5
Source
题意:
有个家伙去看流星雨,不料流星掉下来会砸毁上下左右中五个点。每个流星掉下的位置和时间都不同,求此人能否活命,如果能活命,最短的逃跑时间是多少?
思路:对流星雨排序,然后将地图的每个点的值设为该点最早被炸毁的时间。如果起点一开始就被炸毁了的话,那小文青就直接洗剪吹,否则bfs。
思路:
对流星雨排序,然后将地图的每个点的值设为该点最早被炸毁的时间。如果起点一开始就被炸毁了的话,那这哥们就直接挂掉,否则bfs。
代码:
Source Code
Problem: 3669 User: liangrx06
Memory: 924K Time: 485MS
Language: C++ Result: Accepted
Source Code
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <queue>
using namespace std;
const int N = 302;
const int INF = 10000000;
int map[N+1][N+1];
int pos[5][2] = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}, {0, 0}};
bool legal(int x, int y)
{
return x >= 0 && x <= N && y >= 0 && y <= N;
}
void input()
{
int m;
cin >> m;
int x, y, t;
int i, j;
for (i = 0; i <= N; i ++) {
for (j = 0; j <= N; j ++) {
map[i][j] = INF;
}
}
for (i = 0; i < m; i ++) {
cin >> x >> y >> t;
for (j = 0; j < 5; j ++) {
int nx = x + pos[j][0];
int ny = y + pos[j][1];
if (legal(nx, ny) && t < map[nx][ny])
map[nx][ny] = t;
}
}
}
int BFS()
{
int i, j;
int d[N+1][N+1];
for (i = 0; i <= N; i ++) {
for (j = 0; j <= N; j ++) {
d[i][j] = INF;
}
}
typedef pair<int, int> P;
queue <P> q;
q.push(P(0, 0));
d[0][0] = 0;
while( q.size() ) {
P p = q.front();
q.pop();
int x = p.first;
int y = p.second;
if (map[x][y] == INF)
return d[x][y];
for (i = 0; i < 4; i ++) {
int nx = x + pos[i][0];
int ny = y + pos[i][1];
if (legal(nx, ny) && d[nx][ny] == INF && map[nx][ny] > d[x][y]+1) {
q.push(P(nx, ny));
d[nx][ny] = d[x][y]+1;
}
}
}
return -1;
}
int main(void)
{
input();
printf("%d\n", BFS());
return 0;
}AOJ0121
原文链接地址:
题意:
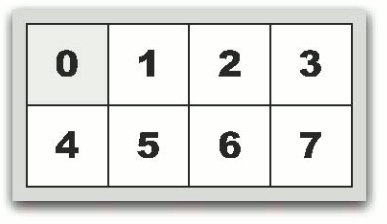
有8个格子,其中7个格子有数分别是1-7,0为空格子。我们要达到的最终状态是0 1 2 3 4 5 6 7,对应于下图:
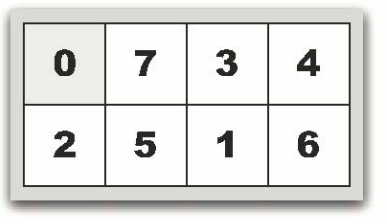
移动格子的规则是,每次可将空格子(也就是0)周围的任意格子移动到该位置。每次移动算一步。比如说,从下图
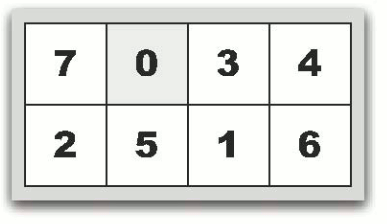
可以移动到状态1
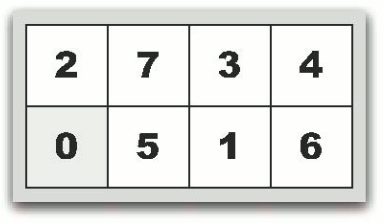
还可以移动到状态2
给定初始状态,求移动到最终状态所需要的移动次数。
思路:
求最短移动次数显然要用BFS,每个状态可以用整形数组、字符串表示,还可以将其编码成一个int数。编码只需要存7个数的位置,每个数的位置有8种,其实对应于7*3个二进制位的状态数,即2^21个状态。合理的编码解码即可。
代码:
#include <iostream>
#include <cstdio>
#include <string>
#include <map>
#include <queue>
#include <algorithm>
using namespace std;
const int INF = 0x3f3f3f3f;
map <string, int> d;
void BFS()
{
queue <string> q;
string s = "01234567";
q.push(s);
d[s] = 0;
while( q.size() ) {
string s = q.front();
q.pop();
int k;
for (k = 0; k < 8; k ++) {
if (s[k] == '0') break;
}
int pos[4] = {1, -1, 4, -4};
for (int i = 0; i < 4; i ++) {
int nk = k + pos[i];
if (k == 3 && nk == 4 || k == 4 && nk == 3)
continue;
if (nk >= 0 && nk < 8) {
string ns = s;
swap(ns[k], ns[nk]);
if (d.find(ns) == d.end()) {
d[ns] = d[s] + 1;
q.push(ns);
}
}
}
}
}
int main(void)
{
BFS();
int a[8];
while (scanf("%d", &a[0]) != EOF) {
string s = "";
s += (a[0] + '0');
for (int i = 1; i < 8; i ++) {
scanf("%d", &a[i]);
s += (a[i] + '0');
}
printf("%d\n", d[s]);
}
return 0;
}

 浙公网安备 33010602011771号
浙公网安备 33010602011771号