《挑战程序设计竞赛》2.2 贪心法-区间 POJ2376 POJ1328 POJ3190
POJ2376
Cleaning Shifts
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 14585 | Accepted: 3718 |
Description
Farmer John is assigning some of his N (1 <= N <= 25,000) cows to do some cleaning chores around the barn. He always wants to have one cow working on cleaning things up and has divided the day into T shifts (1 <= T <= 1,000,000), the first being shift 1 and
the last being shift T.
Each cow is only available at some interval of times during the day for work on cleaning. Any cow that is selected for cleaning duty will work for the entirety of her interval.
Your job is to help Farmer John assign some cows to shifts so that (i) every shift has at least one cow assigned to it, and (ii) as few cows as possible are involved in cleaning. If it is not possible to assign a cow to each shift, print -1.
Each cow is only available at some interval of times during the day for work on cleaning. Any cow that is selected for cleaning duty will work for the entirety of her interval.
Your job is to help Farmer John assign some cows to shifts so that (i) every shift has at least one cow assigned to it, and (ii) as few cows as possible are involved in cleaning. If it is not possible to assign a cow to each shift, print -1.
Input
* Line 1: Two space-separated integers: N and T
* Lines 2..N+1: Each line contains the start and end times of the interval during which a cow can work. A cow starts work at the start time and finishes after the end time.
* Lines 2..N+1: Each line contains the start and end times of the interval during which a cow can work. A cow starts work at the start time and finishes after the end time.
Output
* Line 1: The minimum number of cows Farmer John needs to hire or -1 if it is not possible to assign a cow to each shift.
Sample Input
3 10 1 7 3 6 6 10
Sample Output
2
Hint
This problem has huge input data,use scanf() instead of cin to read data to avoid time limit exceed.
INPUT DETAILS:
There are 3 cows and 10 shifts. Cow #1 can work shifts 1..7, cow #2 can work shifts 3..6, and cow #3 can work shifts 6..10.
OUTPUT DETAILS:
By selecting cows #1 and #3, all shifts are covered. There is no way to cover all the shifts using fewer than 2 cows.
INPUT DETAILS:
There are 3 cows and 10 shifts. Cow #1 can work shifts 1..7, cow #2 can work shifts 3..6, and cow #3 can work shifts 6..10.
OUTPUT DETAILS:
By selecting cows #1 and #3, all shifts are covered. There is no way to cover all the shifts using fewer than 2 cows.
Source
题意
John有N头牛,其土地的耕作时间是1-T,给出每头牛的工作区间,问最少需要几头牛可以满足全部耕作时间都至少有一头牛在工作。
思路
标准区间贪心,先按照每头牛的开始时间排序,每次选开始时间小于未覆盖区间的开始时间的牛中,结束时间最大的那个。
代码
Source Code
Problem: 2376 User: liangrx06
Memory: 1308K Time: 360MS
Language: C++ Result: Accepted
Source Code
#include <iostream>
#include <cstdio>
#include <set>
#include <algorithm>
using namespace std;
typedef pair<int, int> P;
struct cmp {
bool operator()(const P& a, const P& b)const {
return a.first < b.first;
}
};
typedef set<P, cmp> S;
int n, t;
S s;
void input()
{
scanf("%d%d", &n, &t);
s.clear();
int i, b, e;
S::iterator it;
for (i = 0; i < n; i ++) {
scanf("%d%d", &b, &e);
it = s.find(P(b, e));
if (it == s.end())
s.insert(P(b, e));
else if ((*it).second < e) {
s.erase(it);
s.insert(P(b, e));
}
}
//for (it = s.begin(); it != s.end(); it ++)
// cout << (*it).first << " " << (*it).second << endl;
}
int solve()
{
int res = 0;
int begin = 1;
S::iterator it, it1;
while (s.size()) {
int end = 0;
for (it = s.begin(); it != s.end() && (*it).first <= begin; it ++) {
if ((*it).second > end) {
end = (*it).second;
it1 = it;
}
}
if (end == 0) return -1;
s.erase(it1);
begin = end + 1;
//printf("begin=%d\n", begin);
res ++;
if (begin > t)
return res;
}
return -1;
}
int main(void)
{
input();
printf("%d\n", solve());
return 0;
}
POJ1328
Radar Installation
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 67495 | Accepted: 15139 |
Description
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the
sea can be covered by a radius installation, if the distance between them is at most d. We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the
sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
![]() Figure A Sample Input of Radar Installations
Figure A Sample Input of Radar Installations
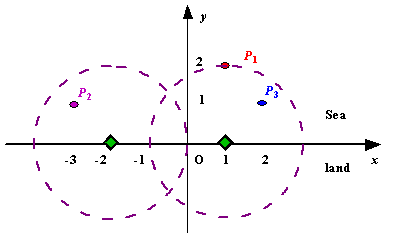 Figure A Sample Input of Radar Installations
Figure A Sample Input of Radar InstallationsInput
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing
two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases. The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2 1 2 -3 1 2 1 1 2 0 2 0 0
Sample Output
Case 1: 2 Case 2: 1
Source
题意:
将一条海岸线看成X轴,X轴上面是大海,海上有若干岛屿,给出雷达的覆盖半径和岛屿的位置,要求在海岸线上建雷达,在雷达能够覆盖全部岛屿情况下,求雷达的最少使用量。
思路:
贪心法求解。先计算雷达覆盖区域与X轴的相交区间(如果不相交则此题解为-1)后,以做区间左值为依据排序。
而后贪心法选择雷达所建位置,下一个雷达建的位置是未覆盖岛屿中最小的区间右值,然后据此更新覆盖的岛屿。
代码:
<pre name="code" class="cpp">Source Code
Problem: 1328 User: liangrx06
Memory: 244K Time: 47MS
Language: C++ Result: Accepted
Source Code
#include <iostream>
#include <cstdio>
#include <cmath>
#include <algorithm>
using namespace std;
const int N = 1000;
struct P {
double x, y;
double l, r;
};
int n;
double d;
P p[N];
int input()
{
cin >> n >> d;
if (!n && !d)
return 0;
int flag = 1;
for (int i = 0; i < n; i ++) {
cin >> p[i].x >> p[i].y;
double z = d*d - p[i].y*p[i].y;
if (z < 0) flag = -1;
z = sqrt(z);
p[i].l = p[i].x - z;
p[i].r = p[i].x + z;
}
if (d < 0) flag = -1;
return flag;
}
bool cmp(const P &a, const P &b)
{
return a.l < b.l;
}
int solve()
{
sort(p, p+n, cmp);
int res = 0, i = 0;
double posL, posR;
while (i < n) {
posL = p[i].l;
posR = p[i].r;
i ++;
while ( i < n && p[i].l <= posR ) {
posL = p[i].l;
posR = (p[i].r < posR) ? p[i].r : posR;
i ++;
}
res ++;
}
return res;
}
int main(void)
{
int c, flag, res;
c = 0;
while ( flag = input() ) {
c ++;
res = -1;
if (flag > 0)
res = solve();
printf("Case %d: %d\n", c, res);
}
return 0;
}POJ3190
Stall Reservations
| Time Limit: 1000MS | Memory Limit: 65536K | |||
| Total Submissions: 4315 | Accepted: 1545 | Special Judge | ||
Description
Oh those picky N (1 <= N <= 50,000) cows! They are so picky that each one will only be milked over some precise time interval A..B (1 <= A <= B <= 1,000,000), which includes both times A and B. Obviously, FJ must create a reservation system to determine which
stall each cow can be assigned for her milking time. Of course, no cow will share such a private moment with other cows. Help FJ by determining:
- The minimum number of stalls required in the barn so that each cow can have her private milking period
- An assignment of cows to these stalls over time
Input
Line 1: A single integer, N Lines 2..N+1: Line i+1 describes cow i's milking interval with two space-separated integers.
Output
Line 1: The minimum number of stalls the barn must have. Lines 2..N+1: Line i+1 describes the stall to which cow i will be assigned for her milking period.
Sample Input
5 1 10 2 4 3 6 5 8 4 7
Sample Output
4 1 2 3 2 4
Hint
Explanation of the sample:
Here's a graphical schedule for this output:
Here's a graphical schedule for this output:
Time 1 2 3 4 5 6 7 8 9 10 Stall 1 c1>>>>>>>>>>>>>>>>>>>>>>>>>>> Stall 2 .. c2>>>>>> c4>>>>>>>>> .. .. Stall 3 .. .. c3>>>>>>>>> .. .. .. .. Stall 4 .. .. .. c5>>>>>>>>> .. .. ..Other outputs using the same number of stalls are possible.
Source
编程算法爱好者。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号