感知机算法(PLA)代码实现
目录
1. 引言
在这里主要实现感知机算法(PLA)的以下几种情况:
- PLA算法的原始形式(二分类)
- PLA算法的对偶形式(二分类)
- PLA算法的作图(二维)
- PLA算法的多分类情况(包括one vs. rest 和one vs. one 两种情况)
- PLA算法的sklearn实现
为了方便起见,使用鸢尾花数据集进行PLA算法的验证。
2. 载入库和数据处理
# 载入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.linear_model import Perceptron
import warnings
warnings.filterwarnings("ignore")
# 设置图形尺寸
plt.rcParams["figure.figsize"] = [14, 7]
plt.rcParams["font.size"] = 14
# 载入鸢尾花数据集
iris_data = load_iris()
xdata = iris_data["data"]
ydata = iris_data["target"]
3. 感知机的原始形式
感知机的详细原理见我的前一篇博客
class model_perceptron(object):
"""
功能:实现感知机算法
参数 w:权重,默认都为None
参数 b:偏置项,默认为0
参数 alpha:学习率,默认为0.001
参数 iter_epoch:迭代轮数,默认最大为1000
"""
def __init__(self, w = None, b = 0, alpha = 0.001, max_iter_epoch = 1000):
self.w = w
self.b = b
self.alpha = alpha
self.max_iter_epoch = max_iter_epoch
def linear_model(self, X):
"""功能:实现线性模型"""
return np.dot(X, self.w) + self.b
def fit(self, X, y):
"""
功能:拟合感知机模型
参数 X:训练集的输入数据
参数 y:训练集的输出数据
"""
# 按训练集的输入维度初始化w
self.w = np.zeros(X.shape[1])
# 误分类的样本就为True
state = np.sign(self.linear_model(X)) != y
# 迭代轮数
total_iter_epoch = 1
while state.any() and (total_iter_epoch <= self.max_iter_epoch):
# 使用误分类点进行权重更新
self.w += self.alpha * y[state][0] * X[state][0]
self.b += self.alpha * y[state][0]
# 状态更新
total_iter_epoch += 1
state = np.sign(self.linear_model(X)) != y
print(f"fit model_perceptron(alpha = {self.alpha}, max_iter_epoch = {self.max_iter_epoch}, total_iter_epoch = {min(self.max_iter_epoch, total_iter_epoch)})")
def predict(self, X):
"""
功能:模型预测
参数 X:测试集的输入数据
"""
return np.sign(self.linear_model(X))
def score(self, X, y):
"""
功能:模型评价(准确率)
参数 X:测试集的输入数据
参数 y:测试集的输出数据
"""
y_predict = self.predict(X)
y_score = (y_predict == y).sum() / len(y)
return y_score
# 二分类的情况(原始形式)/ 数据集的处理与划分
X = xdata[ydata < 2]
y = ydata[ydata < 2]
y = np.where(y == 0, -1, 1)
xtrain, xtest, ytrain, ytest = train_test_split(X, y)
# 原始形式的验证
ppn = model_perceptron()
ppn.fit(xtrain, ytrain)
ppn.predict(xtest)
ppn.score(xtest, ytest)
结果显示(由于随机划分数据集,运行结果不一定和图示相同):

4. 感知机的对偶形式
class perceptron_dual(object):
"""
功能:实现感知机的对偶形式
参数 beta:每个实例点更新的次数组成的向量
参数 b:偏置项,默认为0
参数 alpha:学习率,默认0.001
参数 max_iter_epoch:最大迭代次数,默认为1000
参数 total_iter_epoch:实际迭代次数
"""
def __init__(self, alpha = 0.001, max_iter_epoch = 1000):
self.b = 0
self.alpha = alpha
self.max_iter_epoch = max_iter_epoch
self.total_iter_epoch = 0
def gram_matrix(self, X):
return np.dot(X, self.X.T)
def fit(self, X, y):
# 初始化
self.beta = np.zeros(X.shape[0])
self.X = X
self.y = y
# gram矩阵
gram = self.gram_matrix(X)
# 迭代条件
pred = np.sign(np.dot(gram, self.beta * self.y) + self.b)
state = (pred != y)
while state.any() and (self.total_iter_epoch < self.max_iter_epoch):
# 参数更新
pos = np.arange(len(state))[state][0]
self.beta[pos] += self.alpha
self.b += self.alpha * y[state][0]
# 条件更新
self.total_iter_epoch += 1
pred = np.sign(np.dot(gram, self.beta * y) + self.b)
state = (pred != y)
# fit信息
print(f"fit model perceptron_dual(alpha={self.alpha}, max_iter_epoch={self.max_iter_epoch}, total_iter_epoch={self.total_iter_epoch})")
def predict(self, X):
"""
功能:模型预测
参数 X:测试集的输入数据
"""
gram = self.gram_matrix(X)
pred = np.sign(np.dot(gram, self.beta * self.y) + self.b)
return pred
def score(self, X, y):
"""
功能:模型评价(准确率)
参数 X:测试集的输入数据
参数 y:测试集的输出数据
"""
pred = self.predict(X)
return (pred == y).sum() / len(y)
# 二分类的情况(对偶形式)/ 数据集的处理与划分
X = xdata[ydata < 2]
y = ydata[ydata < 2]
y = np.where(y == 0, -1, 1)
xtrain, xtest, ytrain, ytest = train_test_split(X, y)
# 对偶形式验证
ppn = perceptron_dual()
ppn.fit(xtrain, ytrain)
ppn.predict(xtest)
ppn.score(xtest, ytest)
结果显示(由于随机划分数据集,运行结果不一定和图示相同):

5. 多分类情况—one vs. rest
假设有k个类别,ovr策略是生成k个分类器,最后选取概率最大的预测结果
class perceptron_ovr(object):
"""
功能:实现感知机的多分类情形(采用one vs. rest策略)
参数 w:权重,默认都为None
参数 b:偏置项,默认为0
参数 alpha:学习率,默认0.001
参数 max_iter_epoch:最大迭代次数,默认为1000
"""
def __init__(self, alpha = 0.001, max_iter_epoch = 1000):
self.w = None
self.b = None
self.alpha = alpha
self.max_iter_epoch = max_iter_epoch
def linear_model(self, X):
"""功能:实现线性模型"""
return np.dot(self.w, X.T) + self.b
def fit(self, X, y):
"""
功能:拟合感知机模型
参数 X:训练集的输入数据
参数 y:训练集的输出数据
"""
# 生成各分类器对应的标记
self.y_class = np.unique(y)
y_ovr = np.vstack([np.where(y == i, 1, -1) for i in self.y_class])
# 初始化w, b
self.w = np.zeros([self.y_class.shape[0], X.shape[1]])
self.b = np.zeros([self.y_class.shape[0], 1])
# 拟合各分类器,并更新相应维度的w和b
for index in range(self.y_class.shape[0]):
ppn = model_perceptron(alpha = self.alpha, max_iter_epoch = self.max_iter_epoch)
ppn.fit(X, y_ovr[index])
self.w[index] = ppn.w
self.b[index] = ppn.b
def predict(self, X):
"""
功能:模型预测
参数 X:测试集的输入数据
"""
# 值越大,说明第i维的分类器将该点分得越开,即属于该分类器的概率值越大
y_predict = self.linear_model(X).argmax(axis = 0)
# 还原原数据集的标签
for index in range(self.y_class.shape[0]):
y_predict = np.where(y_predict == index, self.y_class[index], y_predict)
return y_predict
def score(self, X, y):
"""
功能:模型评价(准确率)
参数 X:测试集的输入数据
参数 y:测试集的输出数据
"""
y_score = (self.predict(X) == y).sum()/len(y)
return y_score
# 多分类数据集处理
xtrain, xtest, ytrain, ytest = train_test_split(xdata, ydata)
# one vs. rest的验证
ppn = perceptron_ovr()
ppn.fit(xtrain, ytrain)
ppn.predict(xtest)
ppn.score(xtest, ytest)
结果显示(由于随机划分数据集,运行结果不一定和图示相同):

6. 多分类情况—one vs. one
假设有k个类别,生成k(k-1)/2个二分类器,最后通过多数投票来选取预测结果
from itertools import combinations
class perceptron_ovo(object):
"""
功能:实现感知机的多分类情形(采用one vs. one策略)
参数 w:权重,默认都为None
参数 b:偏置项,默认为0
参数 alpha:学习率,默认0.001
参数 max_iter_epoch:最大迭代次数,默认为1000
"""
def __init__(self, alpha = 0.001, max_iter_epoch = 1000):
self.w = None
self.b = None
self.alpha = alpha
self.max_iter_epoch = max_iter_epoch
def linear_model(self, X):
"""功能:实现线性模型"""
return np.dot(self.w, X.T) + self.b
def fit(self, X, y):
"""
功能:拟合感知机模型
参数 X:训练集的输入数据
参数 y:训练集的输出数据
"""
# 生成各分类器对应的标记(使用排列组合)
self.y_class = np.unique(y)
self.y_combine = [i for i in combinations(self.y_class, 2)]
# 初始化w和b
clf_num = len(self.y_combine)
self.w = np.zeros([clf_num, X.shape[1]])
self.b = np.zeros([clf_num, 1])
for index, label in enumerate(self.y_combine):
# 根据各分类器的标签选取数据集
cond = pd.Series(y).isin(pd.Series(label))
xdata, ydata = X[cond], y[cond]
ydata = np.where(ydata == label[0], 1, -1)
# 拟合各分类器,并更新相应维度的w和b
ppn = model_perceptron(alpha = self.alpha, max_iter_epoch = self.max_iter_epoch)
ppn.fit(xdata, ydata)
self.w[index] = ppn.w
self.b[index] = ppn.b
def voting(self, y):
"""
功能:投票
参数 y:各分类器的预测结果,接受的是元组如(1, 1, 2)
"""
# 统计分类器预测结果的出现次数
y_count = np.unique(np.array(y), return_counts = True)
# 返回出现次数最大的结果位置索引
max_index = y_count[1].argmax()
# 返回某个实例投票后的结果
y_predict = y_count[0][max_index]
return y_predict
def predict(self, X):
"""
功能:模型预测
参数 X:测试集的输入数据
"""
# 预测结果
y_predict = np.sign(self.linear_model(X))
# 还原标签(根据排列组合的标签)
for index, label in enumerate(self.y_combine):
y_predict[index] = np.where(y_predict[index] == 1, label[0], label[1])
# 列为某一个实例的预测结果,打包用于之后的投票
predict_zip = zip(*(i.reshape(-1) for i in np.vsplit(y_predict, self.y_class.shape[0])))
# 投票得到预测结果
y_predict = list(map(lambda x: self.voting(x), list(predict_zip)))
return np.array(y_predict)
def score(self, X, y):
"""
功能:模型评价(准确率)
参数 X:测试集的输入数据
参数 y:测试集的输出数据
"""
y_predict = self.predict(X)
y_score = (y_predict == y).sum() / len(y)
return y_score
# 多分类数据集处理
xtrain, xtest, ytrain, ytest = train_test_split(xdata, ydata)
# one vs. one的验证
ppn = perceptron_ovo()
ppn.fit(xtrain, ytrain)
ppn.predict(xtest)
ppn.score(xtest, ytest)
结果显示(由于随机划分数据集,运行结果不一定和图示相同):

准确率一般比one vs. rest要高,但是生成的分类器多
7. sklearn实现
主要使用sklearn中的Perceptron模块,其中可以实现多分类的情况(默认采用one vs. rest)
from sklearn.linear_model import Perceptron
xtrain, xtest, ytrain, ytest = train_test_split(xdata, ydata)
ppn = Perceptron(max_iter = 1000)
ppn.fit(xtrain, ytrain)
ppn.predict(xtest)
ppn.score(xtest, ytest)
结果显示:

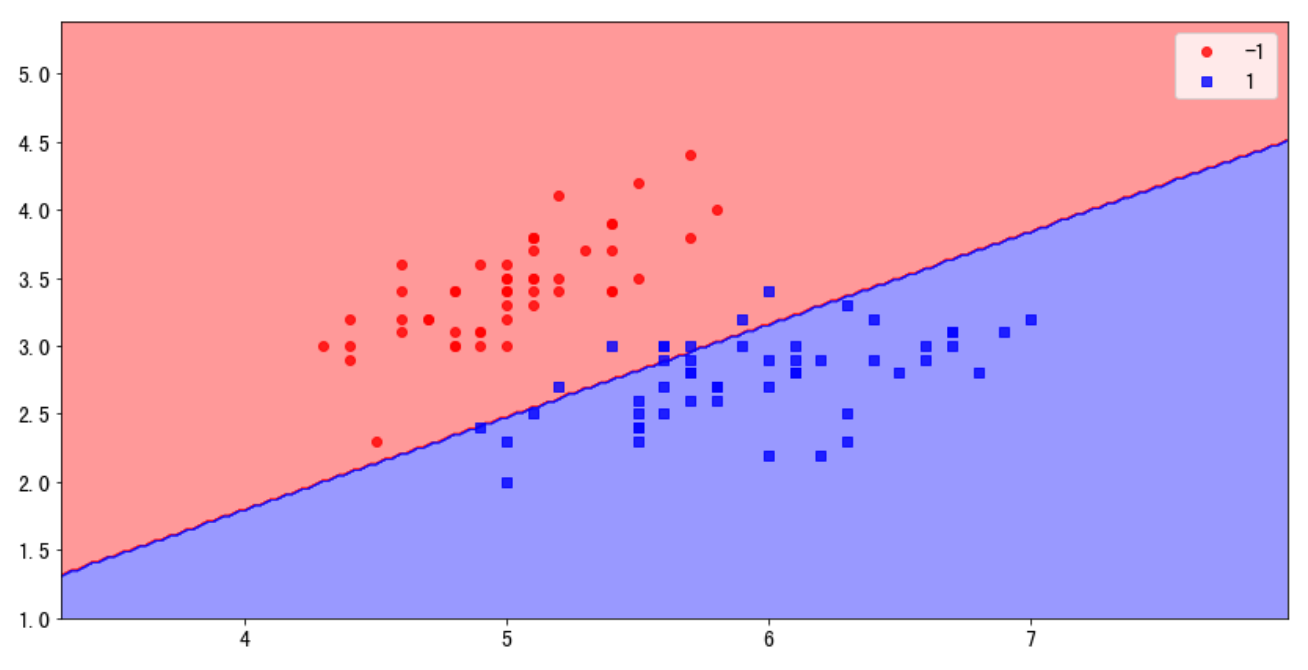
8. 感知机算法的作图
from matplotlib.colors import ListedColormap
def decision_plot(X, Y, clf, test_idx = None, resolution = 0.02):
"""
功能:画分类器的决策图
参数 X:输入实例
参数 Y:实例标记
参数 clf:分类器
参数 test_idx:测试集的index
参数 resolution:np.arange的间隔大小
"""
# 标记和颜色设置
markers = ['o', 's', 'x', '^', '>']
colors = ('red', 'blue', 'lightgreen', 'gray', 'cyan')
cmap = ListedColormap(colors[:len(np.unique(Y))])
# 图形范围
xmin, xmax = X[:, 0].min() - 1, X[:, 0].max() + 1
ymin, ymax = X[:, 1].min() - 1, X[:, 1].max() + 1
x = np.arange(xmin, xmax, resolution)
y = np.arange(ymin, ymax, resolution)
# 网格
nx, ny = np.meshgrid(x, y)
# 数据合并
xdata = np.c_[nx.reshape(-1), ny.reshape(-1)]
# 分类器预测
z = clf.predict(xdata)
z = z.reshape(nx.shape)
# 作区域图
plt.contourf(nx, ny, z, alpha = 0.4, cmap = cmap)
plt.xlim(nx.min(), nx.max())
plt.ylim(ny.min(), ny.max())
# 画点
for index, cl in enumerate(np.unique(Y)):
plt.scatter(x=X[Y == cl, 0], y=X[Y == cl, 1],
alpha=0.8, c = cmap(index),
marker=markers[index], label=cl)
# 突出测试集的点
if test_idx:
X_test, y_test = X[test_idx, :], y[test_idx]
plt.scatter(X_test[:, 0],
X_test[:, 1],
alpha=0.15,
linewidths=2,
marker='^',
edgecolors='black',
facecolors='none',
s=55, label='test set')
# 作图时的数据处理
X = xdata[ydata < 2, :2]
y = ydata[ydata < 2]
y = np.where(y == 0, -1, 1)
xtrain, xtest, ytrain, ytest = train_test_split(X, y)
ppn = model_perceptron()
ppn.fit(xtrain, ytrain)
decision_plot(X, y, ppn)
plt.legend()
结果显示: