深入理解线性模型（一）---基于损失函数的估计

更新时间：2019.10.31

目录

• • 1. 引言
  • 2. 从三个层面来看线性模型
    • 2.1 总体层面
    • 2.2 样本层面
      • 2.2.1 Guass-Markov假设
      • 2.2.2 均值向量
      • 2.2.3 X固定下Y的分布
    • 2.3 数据层面
    • 2.4 其他
  • 3. 基于损失函数的估计
    • 3.1 二次损失
      • 3.1.1 损失函数是最小的
      • 3.1.2 损失函数最小化
    • 3.2 其他损失函数
      • 3.2.1 最小绝对损失
      • 3.2.2 huber函数
      • 3.2.3 分位回归的损失
  • 4. 估计量\(\hat \beta\)的检验
    • 4.1 估计量的评价标准
    • 4.2 无偏性
    • 4.3 有效性
  • 5. \(\sigma^2\)的估计
  • 6. 估计量的区间估计
• 7. 结语

1. 引言

  无论是统计学还是机器学习，我们最先接触的模型（统计中的参数模型，机器学习中的有监督学习）都是线性模型，一个是因为它“简单”，另一个是因为它是其他许多模型的一个衍生基础，这也是为什么实际生活中虽然大多数都是非线性的，而我们还是要学习线性模型的原因。
我最初学习线性模型，觉得线性模型不就是一条直线吗，这很简单啊。然而，这毕竟是一堆天才研究了许多年才出来的东西，这肯定是没有想象中的简单，虽然它的思想确实简单。实际上，有很多模型都可以看做是线性的（即可以写成\(Y = X\beta + \varepsilon\)的形式），虽然它们画出来可能是一条曲线，例如像对数线性回归\(log(y) = \beta_0 + \beta_1x\)，多项式回归\(y = \beta_0 + \beta_1x + \beta_2x^2\)，还有回归解释变量中含有哑变量（定性变量）的情况，回归样条的情况等等都可以看做是线性模型，而这一类模型也被称为广义线性模型。
  对于线性模型我们通常采用最小二乘法来计算，当然这不是说这种方法是最好的。但基于历史的原因，由于以前计算资源的匮乏，手算各种复杂的模型基本是行不通的，但是基于最小二乘法的线性模型的参数估计是有明确表达式的，并且具有优良的统计性质。
  最后，我将分成三篇以三种不同的角度（分别是损失函数、似然函数和贝叶斯估计）来分析线性模型的\(\beta\)和\(\sigma\)这两个参数的估计。而在本篇，是从损失函数的角度出发。

2. 从三个层面来看线性模型

  我们先从总体(理论)，样本(随机变量)和数据三个层面来观察一下一般的线性模型：

2.1 总体层面

  从理论层面上看（无数据）有：

\[Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \cdots + \beta_{p-1}X_{p-1} + \varepsilon \]

  其中，\(Y\)称为响应变量或因变量，\(X_i\)为预测变量/解释变量/自变量，\(\varepsilon\)为随机误差变量。在这里，我们可以把\((X_1, X_2, \cdots , X_{p-1}, Y)\)看做是一个总体,从理论层面上来观测整一个模型。

2.2 样本层面

  假设有\((X_{11}, X_{21}, \cdots , X_{p-1,1}, Y_1),\quad(X_{12}, X_{22}, \cdots , X_{p-1,2}, Y_2),\quad\cdots,\quad(X_{1n}, X_{2n}, \cdots , X_{p-1,n}, Y_n)\)等n个样本，实际上样本也是一个随机向量，那么对于第一层面，我们就可以改写成：

\[Y = \begin{pmatrix} Y_1\\ Y_2\\ \vdots\\ Y_n \end{pmatrix} ,\quad X = \begin{pmatrix} 1 & X_{11} & X_{21} & \cdots & X_{p-1,1}\\ 1 & X_{12} & X_{22} & \cdots & X_{p-1,2}\\ \vdots & \vdots & \vdots & & \vdots \\ 1 & X_{1n} & X_{2n} & \cdots & X_{p-1,n} \end{pmatrix} ,\quad \beta = \begin{pmatrix} \beta_0\\ \beta_1\\ \vdots\\ \beta_{p-1} \end{pmatrix} ,\quad \varepsilon = \begin{pmatrix} \varepsilon_1\\ \varepsilon_2\\ \vdots\\ \varepsilon_n\\ \end{pmatrix} \]

  将上述模型写成矩阵的形式，其中\(X\)被称为设计矩阵

\[Y_{n*1} = X_{n*p}\beta_{p*1} + \varepsilon_{n*1} \]

2.2.1 Guass-Markov假设

  因为我们知道随机变量是可以求期望，求方差的。而在统计中，线性模型是基于诸多主观假定的，其中我们常用的的假定是Guass-Markov假设。它主要假定了随机误差的期望是0，并且同方差，都是\(\sigma^2\)，此外随机误差之间都是无关的。
  将Gauss-Markov假设写成表达式的形式：

1. \(D(\varepsilon_i) = \sigma^2\)
2. \(cov(\varepsilon_i) = 0\)
3. \(E(\varepsilon_i) = 0\)

  其中，如果将假设1和2进行合并，我们就可以将假设简化为

1. \(cov(\varepsilon) = \sigma^2I_n\)
2. \(E(\varepsilon_i) = 0\)

  其中，\(cov(\varepsilon)\)是指随机误差向量的协方差阵，\(I_n\)是\(n*n\)维的单位矩阵。此外，我们在做线性模型的时候，通常都是假设解释变量\(X_i\)之间是无关的

2.2.2 均值向量

  当我们固定X（即相当于知道它的数值）的时候，结合Guass-Markov中\(E(\varepsilon_i) = 0\)的假设，我们可以求得固定\(X\)下\(Y\)的条件期望应该为\(X\beta\)，而实际上\(X\beta\)是我们的理论拟合值\(\hat Y\)。因此，我们也把线性回归称为均值回归.

\[\begin{equation} \begin{cases} Y = X\beta + \varepsilon\\\\ \\\\ E(\varepsilon_i) = 0 \end{cases} => \quad E(Y|X) = E(X\beta + \varepsilon|X) = X\beta + E(\varepsilon) = X\beta \end{equation} \]

  其中，\(E(\varepsilon)\)为零向量

2.2.3 X固定下Y的分布

  实际上，因为X是固定的，\(\beta\)是虽是未知参数，但也是固定的。因此, 有

\[cov(Y) = cov(X\beta + \varepsilon) = cov(\varepsilon) = \sigma^2I_n \]

  说白了，就是\(Y\)满足一个均值为\(X\beta\),方差为\(\sigma^2I_n\)的一个多维分布\(F_n(X\beta, \sigma^2I_n)\)，\(Y_i\)满足一个均值为\(X_i\beta\),方差为\(\sigma^2\)的分布\(F(X_i\beta, \sigma^2)\)

  用图来直观的表示：

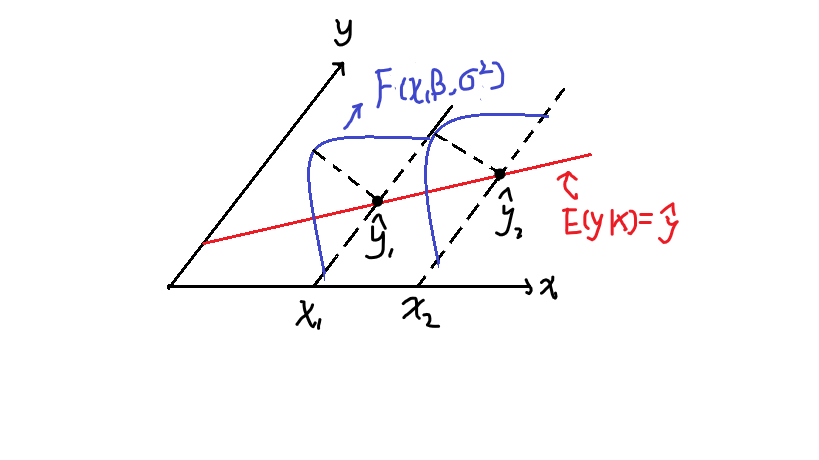
  而当对\(\varepsilon\)加上一个正态性的假设的时候，就能够得到随机误差向量\(\varepsilon\)和\(Y\)满足多维正态分布\(\varepsilon \sim N(O, \sigma^2I_n)\)和\(Y \sim N(X\beta, \sigma^2I_n)\)

2.3 数据层面

  当我们给定观测值 \((x_{11}, x_{21}, \cdots , x_{p-1,1}, y_1),\quad(x_{12}, x_{22}, \cdots , x_{p-1,2}, y_2),\quad\cdots,\quad(x_{1n}, x_{2n}, \cdots , x_{p-1,n}, y_n)\)，我们可以将\(Y\)、\(X\)、\(\beta\)、\(\varepsilon\)表示成：

\[Y = \begin{pmatrix} y_1\\ y_2\\ \vdots\\ y_n \end{pmatrix} ,\quad X = \begin{pmatrix} 1 & x_{11} & x_{21} & \cdots & x_{p-1,1}\\ 1 & x_{12} & x_{22} & \cdots & x_{p-1,2}\\ \vdots & \vdots & \vdots & & \vdots \\ 1 & x_{1n} & x_{2n} & \cdots & x_{p-1,n} \end{pmatrix} ,\quad \beta = \begin{pmatrix} \beta_0\\ \beta_1\\ \vdots\\ \beta_{p-1} \end{pmatrix} ,\quad \varepsilon = \begin{pmatrix} \epsilon_1\\ \epsilon_2\\ \vdots\\ \epsilon_n\\ \end{pmatrix} \]

此时，模型仍可以写成\(Y = X\beta + \varepsilon\)，可是可以通过实际的数值估计出\(\beta\)的值

2.4 其他

  机器学习中有时也写成向量的形式\(f(x) = w^Tx+b\)，将截距和其他回归参数分开，但其实是没有本质的区别的。

3. 基于损失函数的估计

  下面主要是从随机变量的层面出发来继续深入讨论线性模型，
  在数学和计算机领域中，通常是使用损失函数来进行参数的估计，也可以说是模型的拟合。而值得注意的是，我们上述采用了的Guass-Markov假设，在参数\(\beta\)的估计是不需要用到的，这只是在我们之后的检验中需要使用到。但是我们不能说参数\(\beta\)的估计和我们给定的假设没有一点关系，实际上根据不同的假设，我们选定的损失函数也是不同的。这一点，我会在第二篇“基于似然函数的估计”中提到。
  先来谈一下基于损失函数估计的原理：

1. 定义模型中第\(i\)个残差为：\(e_i = y_i - \hat y_i\)，整个残差向量就可以写成：\(e = Y - \hat Y\)，其中，\(\hat Y\)是拟合结果。
2. 主观选择一个损失函数的形式：\(\rho(e_i)\)，又因为损失函数应该是包含待估参数\(\beta\)，因此损失函数又可以写成是\(L(\beta)\)
3. 利用损失函数最小化得到参数的估计：\(\hat \beta = \underset{\beta}{\arg \min} \hspace{1mm} \rho(e_i) = \underset {\beta}{\arg \min} \hspace{1mm} L(\beta)\)，这一串长长的公式是说使得损失函数最小的变元\(\beta\)就是我们所要的估计参数\(\hat \beta\)

3.1 二次损失

  在做线性模型的时候，我们最常使用的是基于二次损失函数的最小二乘法，定义二次损失函数有：\(\sum_{i=1}^n e_i^2\) ，根据我们上面所说的均值回归，以矩阵的形式有：
\begin{equation}
\begin{cases}
L(\beta) = \sum_{i=1}^n e_i^2 = \sum_{i=1}^n(y_i - \hat y_i)^2\\
\\
\hat Y = X\beta
\end{cases}
=> \sum_{i=1}^n (y_i - X_i\beta)^2 = (Y - X\beta)^T(Y - X\beta)
\end{equation}

  进一步化简有（其中，\(Y^TX\beta\)是一个数）：

\[(Y - X\beta)^T(Y - X\beta) = Y^TY - 2Y^TX\beta + \beta^TX^TX\beta \]

  要使损失函数最小化就是对损失函数求导，取到它的最小值（而这个损失函数是一个凸函数）

• tips：值得注意的是，下文中有提到\(\hat Y = X\hat \beta\)，严格来说上面提到的\(\hat Y\)是真实的拟合值，而下文提到的\(\hat Y\)是预测的拟合值

3.1.1 损失函数是最小的

  在求导之前，我们先思考一个问题，为什么\(\sum_{i=1}^n (y_i - X_i\beta)^2\)是最小的（即为什么不选择其他\(\sum_{i=1}^n (y_i - ?)^2\)，为什么前面的要小于等于\(\sum_{i=1}^n (y_i - ?)^2\)）。实际上，这就相当于对于\(E(X - ?)^2\)来说，当?取什么时，这个式子达到最小。而我们知道，当?是\(X\)的期望\(E(X)\)，这个式子就能达到最小。同理（求和和期望只是差了一个系数），对于\(\sum_{i=1}^n (y_i - ?)^2\)）来说，当?是\(Y_i\)的期望\(E(Y_i)\)，这个式子就能达到最小，而这个\(E(Y_i)\)恰好是\(X_i\beta\)，也就是\(\hat Y_i\)实际上是这组数据中，\(Y\)的均值。这样也就保证我们选择的损失函数是在这种二次形式中是最好。

3.1.2 损失函数最小化

  下面对损失函数进行求导：
\begin{equation}
\begin{split}
\frac {\mathrm{d}L(\beta)}{\mathrm{d}\beta} & = \frac {\mathrm{d} Y^TY - 2Y^TX\beta + \beta^TX\beta}{\mathrm{d} \beta}\\
& = 0 - 2X^TY + 2X^TX\beta
\end{split}
\end{equation}

  令\(\frac {\mathrm{d}L(\beta)}{\mathrm{d}\beta} = 0\)，有：

\begin{equation}
0 - 2X^T Y + 2X^TX\beta = 0 => \hat \beta =
\begin{cases}
(X^T X)^{-1} X^TY, & (X^TX)可逆 \\
\\
(X^T X)^- X^TY, & (X^TX)不可逆
\end{cases}
\end{equation}

  正如之前提到的，我们通常假定解释变量\(X_i\)是无关的（即列满秩），此时便有\((X^TX)\)可逆(因为\(Ax=0\)和\(A^TAx=0\)是同解方程组，所以可以证出\(r(A)=r(A^TA)\)的)，所以通常将待估参数表示为\(\hat \beta = (X^TX)^{-1}X^TY\)
  从上述的步骤中，我们是可以看到做估计的时候没有用到Guass-Markov的假设。而在数学和机器学习中，有时也就直接使用参数估计后的模型进行测试，然后求出它的均方误差，并没有对这个估计量做检验。而实际上，\(\hat \beta\)是最佳的线性无偏估计，说它最佳是因为它方差是最小的（检验估计量的有效性中将会提到）。
  最后值得一提的是，上面所述的二次损失形式其实是基于方差齐性\(cov(\varepsilon)=\sigma^2I_n\)的假设，当我们改变这个假设的时候，二次损失的将会有所不同，这个我会在第二篇“基于似然函数的估计”中会进一步提到。

3.2 其他损失函数

  既然提到了二次损失，在这里也提一下其他的一些损失函数

3.2.1 最小绝对损失

  定义为：\(L(\beta) = \sum_{i=1}^n |y_i - x_i\beta|\)，也叫一次损失
  此外，对于\(E(|y_i - ?|)\)，当？取中位数的时候，这个损失函数是最小的，所以有时也称为最小中位估计。而由于中位数比平均数要稳健，所以对比二次损失，绝对损失对异常点不敏感。当然这里，当我们假定\(\varepsilon\)是服从均值为0的正态分布的时候，\(X\beta\)实际上也是固定X下Y的中位数

3.2.2 huber函数

  huber函数主要是用于稳健回归的，其中绝对损失其实就是huber函数的一个特例，它的图像如下：

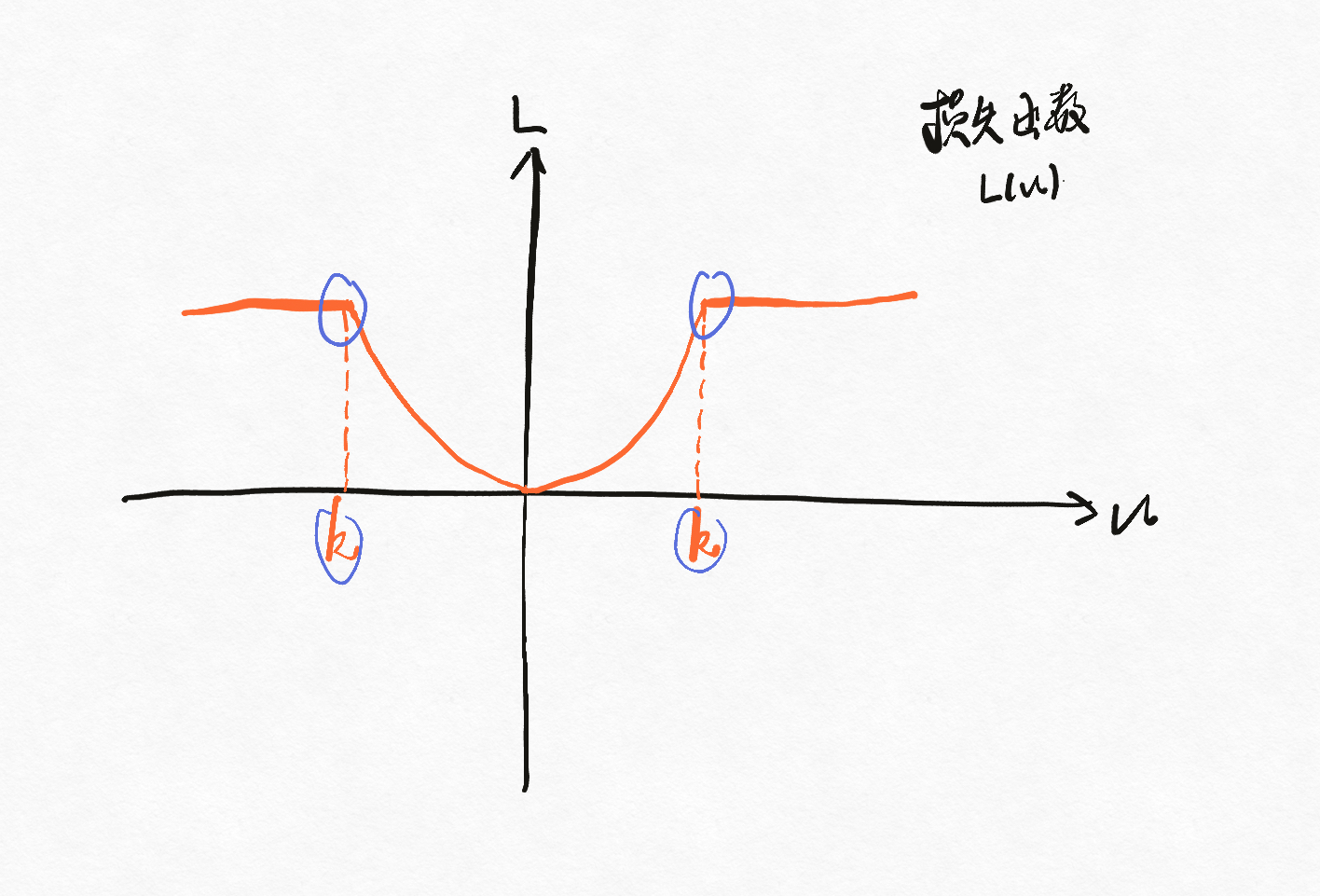
  可以看见当u到一定程度的时候，它的损失是呈水平的，而异常点是指那些远离理论拟合值的观测点，即指u很大的点，这一说明了huber函数的稳健（对异常点不敏感）。当然huber函数也存在一定的缺陷，像多一个参数k，还有不光滑的部分。

3.2.3 分位回归的损失

  定义为：\(L(\beta) = \sum_{i=1}^n e_i(\tau - I(e_i < 0))\)，其中I()是指示函数，\(0 < \tau < 1\)。上面所述的都是对称的损失函数，但是分位回归的损失函数是不对称的，实际上不对称带来的影响会左右曲线的拟合，这时就需要使用分位回归的损失。
  正如下面这个图所示：

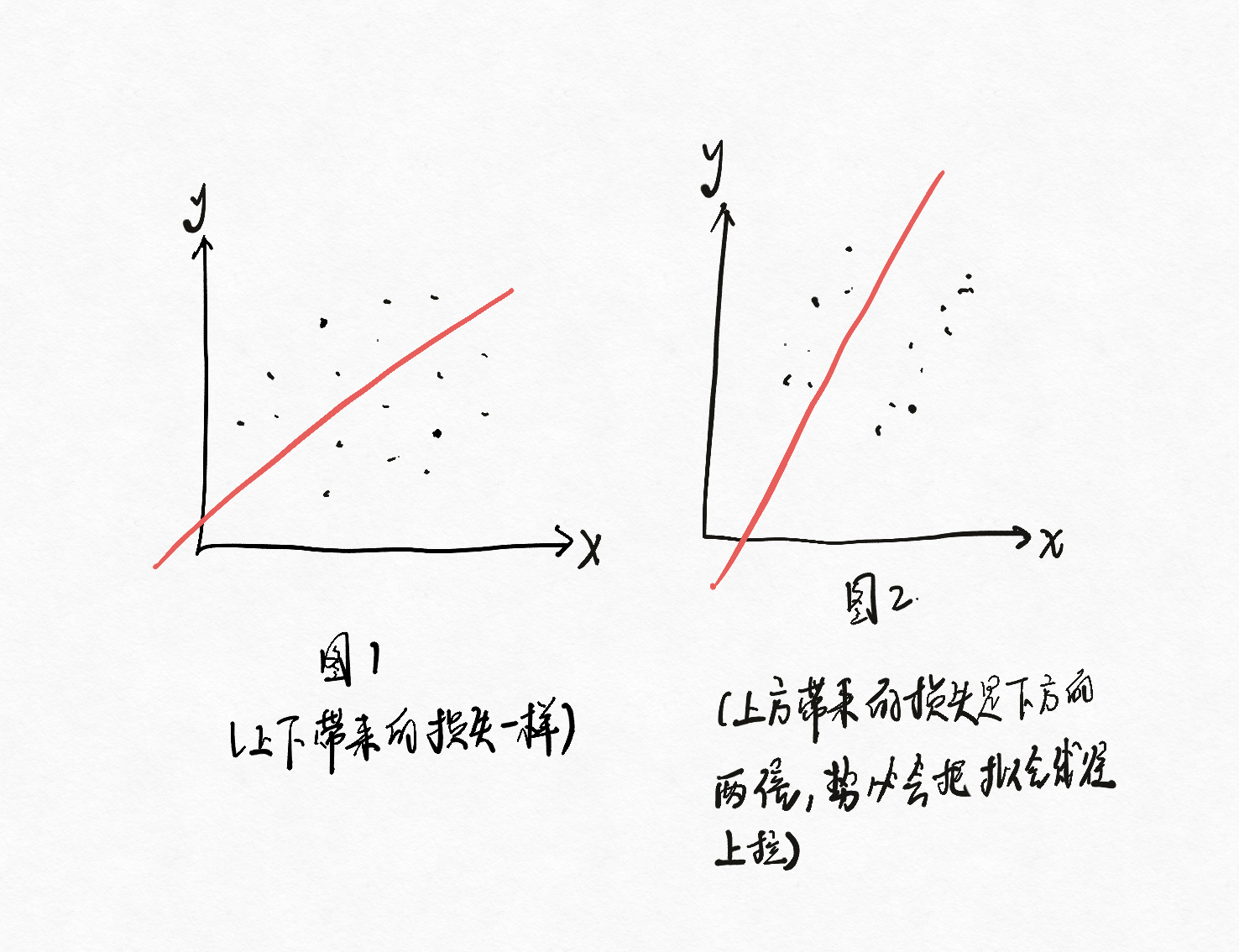
  实际上，绝对损失同样也可以看做是分位回归的损失函数的一个特例，当\(\tau\)取0.5时，两者实际上就差了一个常数。

4. 估计量\(\hat \beta\)的检验

  谈过估计之后，继续谈一下估计量\(\hat \beta\)的检验，而实际上这个估计是最佳线性无偏估计

4.1 估计量的评价标准

  估计量的评价标准主要有三个，无偏性、有效性、一致性。以这里的\(\hat \beta\)为例，

• 无偏性指的是估计量的期望等于参数的真实值，即\(E(\hat \beta) = \beta\)，其中\(\beta\)实际上是一个随机向量，因为X是固定的，而Y是随机向量。
• 有效性是指在诸多无偏估计中，方差最小的那一个估计量。
• 一致性是描述当样本容量无穷时，估计量限接近参数的真实值，即\(n-> + \infty, \hat \beta -> \beta\)，表示成数学语言就是\(P \underset{n-> + \infty}(|\hat \beta - \beta| < \varepsilon) = 1\)。
    在这之中，一致性是最容易满足的，其次是无偏性，最后才是有效性。在这里，只讨论无偏性和有效性

4.2 无偏性

  讨论这个估计是否是无偏估计

\[E(\hat \beta) = E((X^TX)^{-1}X^TY) = (X^TX)^{-1}X^TE(Y) = (X^TX)^{-1}X^TX\beta = \beta \]

4.3 有效性

  经过上面的证明，我们可以得到：

\[ \hat Y = X \hat \beta = X(X^TX)^{-1}X^TY = HY \]

  其中，记\(H = X(X^TX)^{-1}X^T\)，且称\(H\)为帽子矩阵，这个帽子矩阵有优良的性质，是一个幂等对称矩阵。即有\(H^T = H\)、\(H^2 = H\)。此外，也把\(H\)称为投影矩阵，即可以将随机向量\(Y\)投影到\(X\)的超平面上。
  再来看一幅图

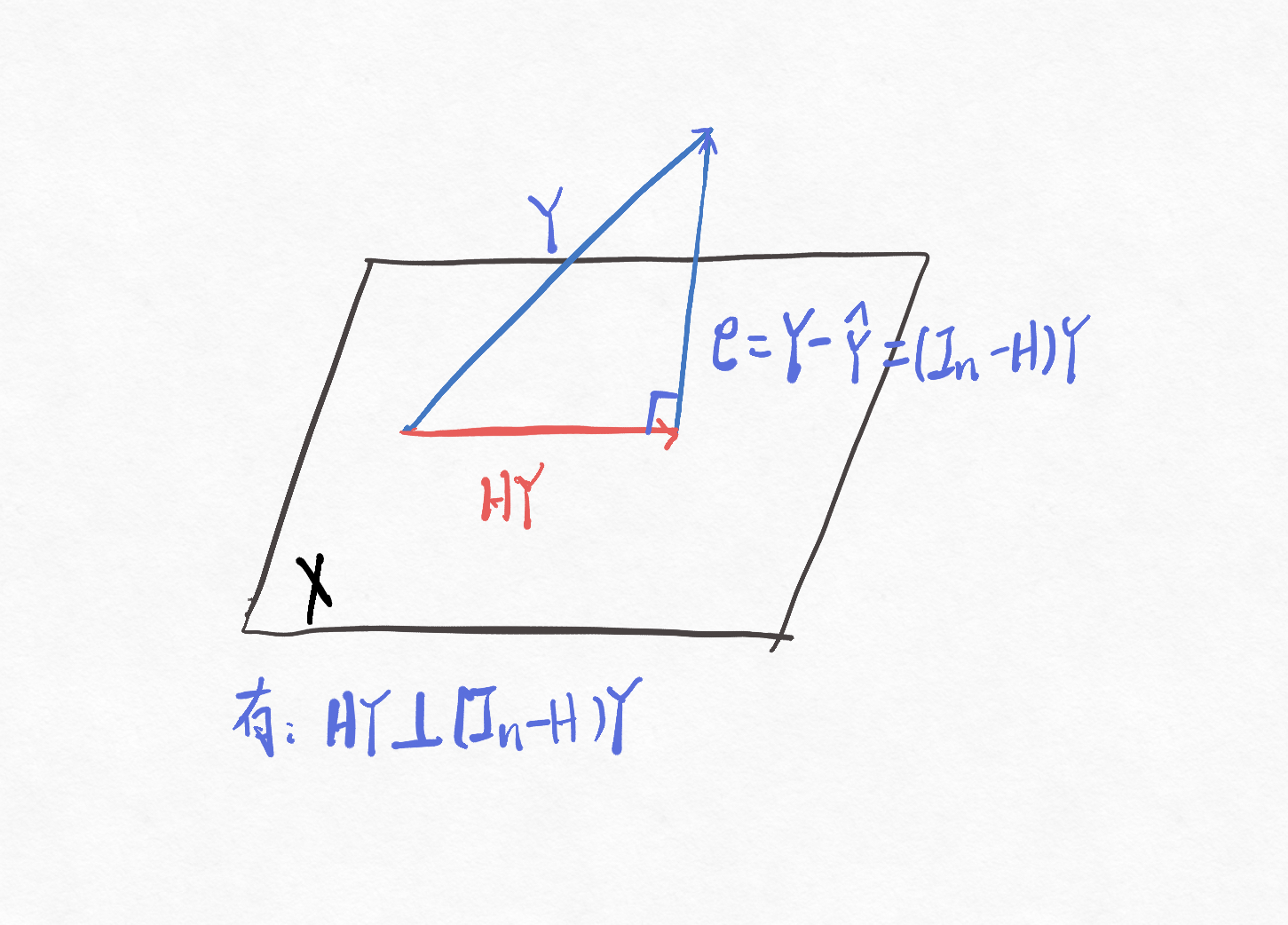
  我们知道当垂直时，线段到平面的距离是最短的。即当\(HY\perp(I_n - H)Y\)时，残差\(e\)是最小的，这也直观地证明这个估计是方差最小的（因为残差\(e\)是方差的一个度量），因此我们也称这个估计\(\hat \beta\)是一切线性无偏估计中方差最小的。
  既然\(\hat \beta\)是最小的，那么下面来推导下它的方差究竟是多少
\begin{equation}
\begin{split}
cov(\hat \beta) & = cov((X^T X)^{-1} X^T Y)\\
& = (X^T X)^{-1} X^T cov(Y) X (X^T X)^{-1}\\
& = (X^T X)^{-1} X^T \sigma^2 I_n X (X^T X)^{-1}\\
& = \sigma^2 (X^T X)^{-1}
\end{split}
\end{equation}

  因此，根据\(\hat \beta_i\)的协方差，我们可以得到\(\hat \beta_i\)的标准误差为：

\[st.dev(\hat \beta_i) = \sigma \sqrt{(X^TX)^{-1}_{ii}} \]

  在这里，我们终于见到了假设中的\(\sigma\)(同方差)，而这正也说明了我之前所说的估计\(\beta\)不用假设，但是检验的时候就需要用到

5. \(\sigma^2\)的估计

  虽然算出了\(\hat \beta_i\)的标准误差，但是它表达式中的\(\sigma\)实际上是一个未知参数，下面对其进行估计。我们知道方差是指偏离平均水平的程度，因此我们很自然地想到使用\(\frac{\displaystyle \sum_{i=1}^n(y_i - \hat y_i)^2}{n}\)来估计，即使用\(\frac{\displaystyle \sum_{i=1}^n(e_i)^2}{n}\)来估计，因为我们之前说过\(\hat Y\)是X固定下Y的平均水平。因此，有
\begin{equation}
\begin{split}
\displaystyle \sum_{i=1}^n (e_i)^2 & = e^T e\\
& = Y^T(I_n - H)^T(I_n - H)Y \\
& = Y^T(I_n - H)Y
\end{split}
\end{equation}

  其中，由于\(H\)是幂等对称阵，所以\((I_n - H)\)实际上也是幂等对称阵。
  下面给出两种证法：
  证法1：
\begin{equation}
\begin{split}
E(Y^T(I_n - H)Y) & = E(tr(Y^T (I_n - H)Y))\\
& = E[tr(YY^T (I_n - H))]\\
& = tr[(I_n - H)E(YY^T)]\\
& = tr(I_n - H)[cov(Y) + E(Y)E(Y)^T]\\
& = tr(I_n - H)[\sigma^2I_n + X\beta \beta^T XT]\\
& = (n-p)\sigma^2 + tr[(I_n - H)X\beta \beta^T XT]\\
& = (n-p)\sigma^2 + tr[(I_n - X(X^T X)^{-1} X^T)X\beta \beta^T XT]\\
& = (n-p)\sigma^2
\end{split}
\end{equation}

  证法2：
  \begin{equation}
\begin{split}
E(Y^T(I_n - H)Y) & = E(tr(Y^T(I_n - H)Y))\\
& = E(Y^T)(I_n - H)E(Y) + tr((I_n - H)cov(Y))\\
& = \beta^T X^T(I_n - H)X\beta + (n-p)\sigma^2\\
& = \beta^TX ^T(I_n - X(X^T X)^{-1} X^T)X\beta + (n-p)\sigma^2\\
& = (n-p)\sigma^2
\end{split}
\end{equation}

  其中，由于帽子矩阵的是幂等阵，所以特征值只有0或者1，设有p个特征值为1，因此\(I_n - H\)有n-p个特征值为1，即\(tr(I_n - H) = n-p\)。实际上，当X列满秩的时候，有\(tr(H) = tr(X(X^TX)^{-1}X^T) = tr(X^TX(X^TX)^{-1}) = tr(I_p) = p\)，因此可以看出H的秩等于\(X\)的维数，也等于\(X\)的变量个数加上常数。在这里，我们也更加清楚，为什么我们要假设解释变量\(X_i\)都是无关的。
  由上面的推导过程可以看出，\(\sigma^2\)的无偏估计应该是\(\frac {\displaystyle \sum_{i=1}^n e_i}{n-p}\)，将残差平方和\(\displaystyle \sum_{i=1}^n e_i\)记为\(SSE\)，并且记均方误差为\(MSE\)，即有：

\[\hat \sigma^2 = \frac {SSE}{n-p} = MSE \]

  其中\(p\)为变量个数加上常数个数（即设计矩阵\(X\)的维数）

6. 估计量的区间估计

  上面是做的估计都是点估计，下面谈谈怎么做区间估计
  我们的目标是找到\(\bar \beta\)和\(\underline \beta\)，使得

\[P(\bar \beta_i < \beta_i < \underline \beta_i) = 1 - \alpha \]

  为了实现这一目标，我们来构造含未知参数\(\beta\)的枢轴量
  对于\(\beta_i\)，我们可以对它进行标准化，有：

\[\frac {\hat \beta_i - \beta_i}{\sigma \sqrt{(X^TX)^{-1}_{ii}}} \sim N(0, 1) \tag{I} \]

  此外，我们考虑\(\frac{\hat \sigma}{\sigma}\)

\[ \frac{\hat \sigma}{\sigma} = \sqrt{\frac {\frac {\displaystyle \sum_{i=1}^n (y_i - \hat y_i)^2}{n-p}}{\sigma^2}} = \sqrt{\frac {\displaystyle \sum_{i=1}^n (\frac {y_i - \hat y_i}{\sigma})^2}{n-p}} \tag{II} \]

  其中，\(\displaystyle \sum_{i=1}^n (\frac {y_i - \hat y_i}{\sigma})^2 \sim \chi^2(n-p)\)
  将上述(I)和(II)结合起来，有

\[\frac {\hat \beta_i - \beta_i}{\hat \sigma \sqrt{(X^TX)^{-1}_{ii}}} = \frac{\frac {\hat \beta_i - \beta_i}{\sigma \sqrt{(X^TX)^{-1}_{ii}}}} {\frac {\hat \sigma}{\sigma}} = \frac{\frac {\hat \beta_i - \beta_i}{\sigma \sqrt{(X^TX)^{-1}_{ii}}}} {\sqrt{\frac {\displaystyle \sum_{i=1}^n (\frac {y_i - \hat y_i}{\sigma})^2}{n-p}}} \sim t(n-p) \]

  即有区间估计，\(\beta_i \underline + t_{1 - \frac{\alpha}{2}}(n-p) \hat{st.dev}(\hat \beta)\)

7. 结语

  虽然最小二乘法的估计有明确的表达式，但是实际用计算机来拟合模型的时候，都不是直接用它估计的表达式来计算的，而是使用梯度下降的方法来加快收敛速度。在李航那本经典的小蓝书，有提到到统计学习方法的三要素分别是：模型、策略和算法。对应这里实际上就是，模型是指线性模型，策略是指损失函数最小，而算法就是计算机实现这一模型的方法，也就是梯度下降算法。