201971010118-梁春云 实验三 结对项目《{0-1}KP 实例数据集算法实验平台》项目报告
| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | [https://edu.cnblogs.com/campus/xbsf/2019nwnucs] |
| 这个作业要求链接 | [https://edu.cnblogs.com/campus/xbsf/2019nwnucs/homework/12560] |
| 我的课程学习目标 | (1)体验软件项目开发中的两人合作,练习结对编程;(2)掌握Github协作开发软件的操作方法 |
| 对学习目标的帮助 | (1)通过结对编程,了解和学习结对编程的方法;(2)熟悉以及掌握Github协作开发的操作方法 |
| 结对方学号-姓名 | 201971010121-李健康 |
| 结对方本次博客作业链接 | https://www.cnblogs.com/yingyaoyao/p/16090655.html |
| 本项目Github的仓库链接地址 | https://github.com/yingyaoyao/Is-Cool-3 |
-
任务一 阅读《现代软件工程—构建之法》第3-4章内容,理解并掌握代码风格规范、代码设计规范、代码复审、结对编程概念;
-
代码风格规范
代码风格的原则是:简明,易读,无二义性。
1.缩进:4个空格,在Visual Studio和其他的一些编辑工具中都可以定义Tab键扩展成为几个空格键
2.行宽:行宽必须限制,可以限定为100字符
3.括号:在复杂的条件表达式中,用括号清楚地表示逻辑优先级
4.断行与空白的{}行:每个{}独占一行,清晰地表示程序结构
5.分行:不把多条语句放在一行上,不要把多个变量定义在一行上
6.命名:在变量名中不要提到类型或其他语法方面的描述,命名精简
7.下划线:用来分隔变量名字中的作用域标注和变量的语义
8.大小写:由多个单词组成的变量名,如果全部大小写,不易读
9.注释:复杂的注释应该放在函数前面,注释应随着程序更改而更改 -
代码设计规范
代码设计规范不光是程序书写的格式问题,牵涉程序设计、模块之间的关系。
1.函数
2.goto函数做好有单一的出口,为到达这一目的,可以使用goto
3.错误处理:参数处理;断言 -
代码复审
代码复审:看代码是否在代码规范的框架内正确地解决了问题。
代码复审的形式名称 形式 目的 自我复审 自己vs.自己 用同伴复审的标准来要求自己。不一定最有效。 同伴复审 复审者vs.开发者 简便易行 团队复审 团对vs.开发者 有比较严格的规定和流程,适用于关键的代码,以及复审后不在更新的代码 代码复审的步骤
1.代码必须成功编译,在所有要求的平台上,同时编译Debug|Retail版本。编译团队规定的最严格的编译警告等级。
2.程序员必须测试过代码。最好的方法是在调试器中单步执行。
3.程序员必须提供新的代码,以及文件差异分析工具。用Windiff或VSTS自带的工具都可以.VSTS 中可以通过Shelveset来支持远程代码复审。在复审中,复审者可以选择面对面的复审、独立复审或其他方式。
4.在面对面的复审中,一般是开发者控制流程,讲述修改的前因后果。但是复审者有权在任何时候打断叙述,提出自己的意见。
5.复审者必须逐一提供反馈意见。
6.开发者必须负责让所有的问题都得到满意的解释或解答,或者在TFS中创建新的工作项以确保这些问题会得到处理。
7.对于复审的结果,双方必须达成一致的意见。 -
结对编程
结对编程:是一种敏捷软件开发的方法,两个程序员在一个计算机上共同工作。一个人输入代码,而另一个人审查他输入的每一行代码。输入代码的人称作驾驶员,审查代码的人称作观察员(或导航员)。两个程序员经常互换角色。在结对编程中,观察员同时考虑工作的战略性方向,提出改进的意见,或将来可能出现的问题以便处理。这样使得驾驶者可以集中全部注意力在完成当前任务的“战术”方面。观察员当作安全网和指南。结对编程对开发程序有很多好处。比如增加纪律性,写出更好的代码等。
-
-
任务二 两两自由结对,对结对方《实验二 软件工程个人项目》的项目成果进行评价
-
结对伙伴:
-
克隆结对方项目源码到本地机器,阅读并测试运行代码,参照《现代软件工程—构建之法》4.4.3节核查表复审同伴项目代码并记录。

-
依据复审结果尝试利用github的Fork、Clone、Push、Pull request、Merge pull request等操作对同伴个人项目仓库的源码进行合作修改。

-
-
任务三 采用两人结对编程方式,设计开发一款{0-1}KP 实例数据集算法实验平台。
-
1.需求分析陈述
(1)可正确读入实验数据文件的有效{0-1}KP数据;{0-1}KP 实例数据集需存储在数据库;
(2)能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图;
(3)能够对一组{0-1}KP数据按重量比进行非递增排序;
(4)用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位);
(5)任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
(6)平台可动态嵌入任何一个有效的{0-1}KP 实例求解算法,并保存算法实验日志数据;人机交互界面要求为GUI界面(WEB页面、APP页面都可); -
2.软件设计说明
此次采用结对编程的方法,设计以及开发了一款实例数据的算法实现平台,在数据的存储方面需存储在数据库,其次人机交互界面要求为GUI界面,同时在本次的算法实验平台之上可以嵌入任何一个有效的{0-1}KP实例求解算法,并保存算法实验日志数据。
(1)遗传算法:遗传算法最早是由美国的 John holland于20世纪70年代提出,该算法是根据大自然中生物体进化规律而设计提出的。是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
(2)遗传算法特点:(1)算法从问题解的串集开始搜索,而不是从单个解开始。这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。遗传算法从串集开始搜索,覆盖面大,利于全局择优。(2)遗传算法同时处理群体中的多个个体,即对搜索空间中的多个解进行评估,减少了陷入局部最优解的风险,同时算法本身易于实现并行化。(3)遗传算法基本上不用搜索空间的知识或其它辅助信息,而仅用适应度函数值来评估个体,在此基础上进行遗传操作。适应度函数不仅不受连续可微的约束,而且其定义域可以任意设定。这一特点使得遗传算法的应用范围大大扩展。 (4)遗传算法不是采用确定性规则,而是采用概率的变迁规则来指导他的搜索方向。 (5)具有自组织、自适应和自学习性。遗传算法利用进化过程获得的信息自行组织搜索时,适应度大的个体具有较高的生存概率,并获得更适应环境的基因结构。 (6)此外,算法本身也可以采用动态自适应技术,在进化过程中自动调整算法控制参数和编码精度,比如使用模糊自适应法。
(3)遗传算法的基本运算过程:(1)初始化:设置进化代数计数器t=0,设置最大进化代数T,随机生成M个个体作为初始群体P(0)。(2)个体评价:计算群体P(t)中各个个体的适应度。(3)选择运算:将选择算子作用于群体。选择的目的是把优化的个体直接遗传到下一代或通过配对交叉产生新的个体再遗传到下一代。选择操作是建立在群体中个体的适应度评估基础上的。(4)交叉运算:将交叉算子作用于群体。遗传算法中起核心作用的就是交叉算子。(5)变异运算:将变异算子作用于群体。即是对群体中的个体串的某些基因座上的基因值作变动。群体P(t)经过选择、交叉、变异运算之后得到下一代群体P(t+1)。(6)终止条件判断:若t=T,则以进化过程中所得到的具有最大适应度个体作为最优解输出,终止计算。
(4)遗传算法的过程图解
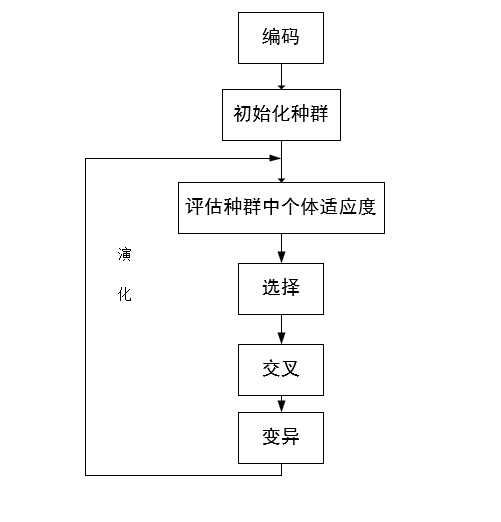
(5)遗传算法各函数
-
Drawfunc函数
function Drawfunc(label)
x=-5:0.05:5;%41列的向量
if label==1
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Rastrigin([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
if label==2
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Schaffer([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
if label==3
y = x;
[X,Y] = meshgrid(x,y);
[row,col] = size(X);
for l = 1 :col
for h = 1 :row
z(h,l) = Griewank([X(h,l),Y(h,l)]);
end
end
surf(X,Y,z);
shading interp
xlabel('x1-axis'),ylabel('x2-axis'),zlabel('f-axis');
title('mesh');
end
fun函数
function y = fun(x,label)
%函数用于计算粒子适应度值
%x input 输入粒子
%y output 粒子适应度值
if label==1
y=-Rastrigin(x);
elseif label==2
y=-Schaffer(x);
else
y=-Griewank(x);
end
Griewank函数
function y=Griewank(x)
%Griewan函数
%输入x,给出相应的y值,在x=(0,0,…,0)处有全局极小点0.
%编制人:
%编制日期:
[row,col]=size(x);
if row>1
error('输入的参数错误');
end
y1=1/4000*sum(x.^2);
y2=1;
for h=1:col
y2=y2*cos(x(h)/sqrt(h));
end
y=y1-y2+1;
%y=-y;
Rastrigin函数
function y = Rastrigin(x)
% Rastrigin函数
% 输入x,给出相应的y值,在x = ( 0 , 0 ,…, 0 )处有全局极小点0.
% 编制人:
% 编制日期:
[row,col] = size(x);
if row > 1
error( ' 输入的参数错误 ' );
end
y =sum(x.^2-10*cos(2*pi*x)+10);
%y =-y;
- 3.软件实现及核心功能代码展示
(1)算法实现
动态规划
class onezerobag:
def __init__(self, w, v, c):
self.w = w
self.v = v
self.c = c
def dynamic_programming(self):
self.v = np.array(self.v)
self.w = np.array(self.w)
num = self.v.size # 物体数量
values = np.zeros([num + 1, self.c + 1])
for i in range(values.shape[0]):
values[i, 0] = 0
for i in range(values.shape[1]):
values[0, i] = 0
for i in range(1, values.shape[0], 1):
for j in range(1, values.shape[1], 1):
if (self.w[i - 1] > j): # 如果物体重量大于包当前重量,不装进去
values[i, j] = values[i - 1, j]
else:
if (values[i - 1, j] >
values[i - 1, j - self.w[i - 1]] + self.v[i - 1]):
values[i, j] = values[i - 1, j]
else:
values[i,
j] = values[i - 1,
j - self.w[i - 1]] + self.v[i - 1]
return values
def load_which(self, values):
h = values.shape[0]
c = self.c
which = []
for i in range(h - 1, 0, -1):
if (values[i, c] == values[i - 1, c]):
continue
else:
which.append(i)
c = c - self.w[i - 1]
which.reverse()
return which, values[values.shape[0] - 1, values.shape[1] - 1]
回溯法
class backTrackingMethod:
def __init__(self, w, v, c, cw, cp, bestp):
self.w = np.array(w)
self.v = np.array(v)
self.c = c
self.cw = cw
self.cp = cp
self.bestp = bestp
def value_per(self):
per = self.v / self.w
sor = np.sort(per)
index = np.argsort(per)
list = []
for i in sor:
list.append(i)
list.reverse()
list1 = []
for i in index:
list1.append(i)
list1.reverse()
index = np.array(list1)
a = self.v.copy()
b = self.w.copy()
for i in range(self.v.size):
a[i] = self.v[index[i]]
b[i] = self.w[index[i]]
self.v = a.copy()
self.w = b.copy()
return self.v, self.w, index
def bound(self, i):
leftw = self.c - self.cw
bestbound = self.cp
while (i < self.v.size):
if (self.w[i] <= leftw):
bestbound = bestbound + self.v[i]
leftw = leftw - self.w[i]
i += 1
else:
bestbound = bestbound + self.v[i] / self.w[i] * leftw
break
return bestbound
def back_tracking(self, i, visit):
if (i > self.v.size - 1):
self.bestp = self.cp
return
if (self.cw + self.w[i] < self.c):
self.cw += self.w[i]
self.cp += self.v[i]
visit[i] = 1
self.back_tracking(i + 1, visit)
self.cw -= self.w[i]
self.cp -= self.v[i]
else:
visit[i] = 0
if (self.bound(i + 1) >= self.bestp):
self.back_tracking(i + 1, visit)
return visit, self.bestp
贪心法
class Good:
def __init__(self, w, v, c):
self.w = w
self.v = v
self.c = c
def greed(goods,total):
result=[]
while True;
s=strategy(goods,total)
if s==-1:
result.append(goods[s].weight)
total= total-goods[s].weight
goods[s].c=1
return result
def strategy(goods,total):
index = -1
minWeight=goods[0].weight
for i in range(0,len(goods)):
currentGood = goods[i]
if currentGood.c==0 and currentGood.weight <= total and currentGood.weight<=minWeight:
index = i
minWeight =goods[index].weight
return index
按性价比进行非递增排序
w_np = np.array(weight)
p_np = np.array(profit)
ratio = p_np / w_np
print("价值与重量之比:")
for a in ratio:
print(format(a, '.3f'), end=" ")
print("\n\n非递增排序后:")
res = sorted(ratio, reverse=True)
for b in res:
print(format(b, '.3f'), end=" ")
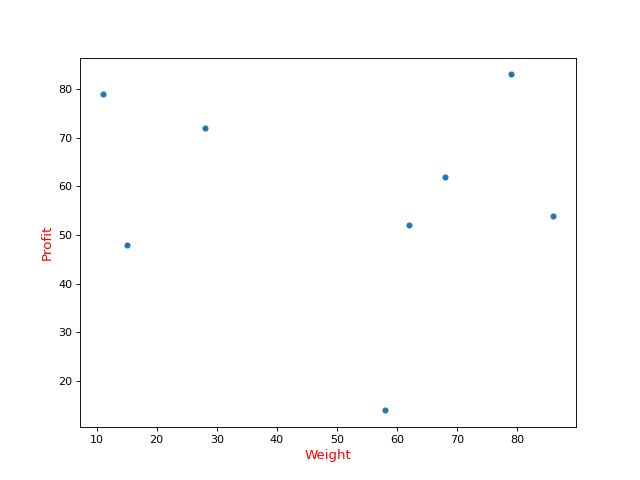
散点图绘制
plt.figure(figsize=(8, 6), dpi=80)
plt.scatter(weight, profit, s=20)
plt.xlabel("Weight", fontsize=12, color="r")
plt.ylabel("Profit", fontsize=12, color='r')
plt.show()
GUI界面
root = tk.Tk()
root.title('实验三 软件工程结对项目')
root.geometry('500x500')
lb = Label(root,text='D{0-1}KP 实例数据集算法实验平台', bg='#d3fbfb', fg='red',
font=('华文新魏',18), width=80, height=2, relief=SUNKEN)
lb.pack()
menubar=Menu(root)
femnu1=Menu(root)
for item in['新建','打开','保存','另存为']:
femnu1.add_command(label=item)
femnu2=Menu(root)
for item in ['复制','粘贴','剪贴']:
femnu2.add_command(label=item)
femnu3=Menu(root)
for item in ['大纲视图','web视图']:
femnu3.add_command(label=item)
femnu4=Menu(root)
for item in ["版权信息","其他说明"]:
femnu4.add_command(label=item)
menubar.add_cascade(label="文件",menu=femnu1)
menubar.add_cascade(label="编辑",menu=femnu2)
menubar.add_cascade(label="视图",menu=femnu3)
menubar.add_cascade(label="关于",menu=femnu4)
root.config(menu=menubar)
root.mainloop
var = tk.IntVar()
def Mysel():
dic = {0:'散点图', 1:'动态规划算法', 2:'回溯法'}
s = "您选了" + dic.get(var.get()) + "文件"
lb.config(text = s)
var = IntVar()
rd1 = Radiobutton(root,text="散点图",variable=var,value=0,command=Mysel)
rd1.pack()
rd2 = Radiobutton(root,text="动态规划算法",variable=var,value=1,command=Mysel)
rd2.pack()
rd3 = Radiobutton(root,text="回溯法",variable=var,value=2,command=Mysel)
rd3.pack()
root.mainloop()
- 4.实验测试运行
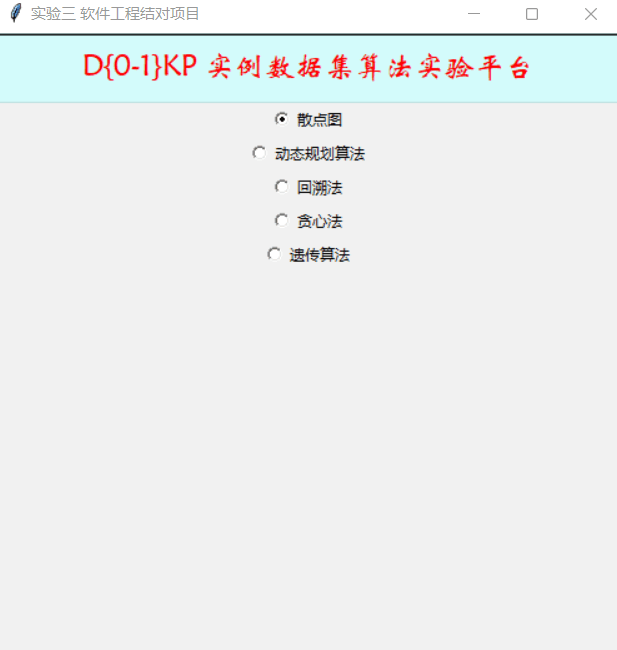
选择算法
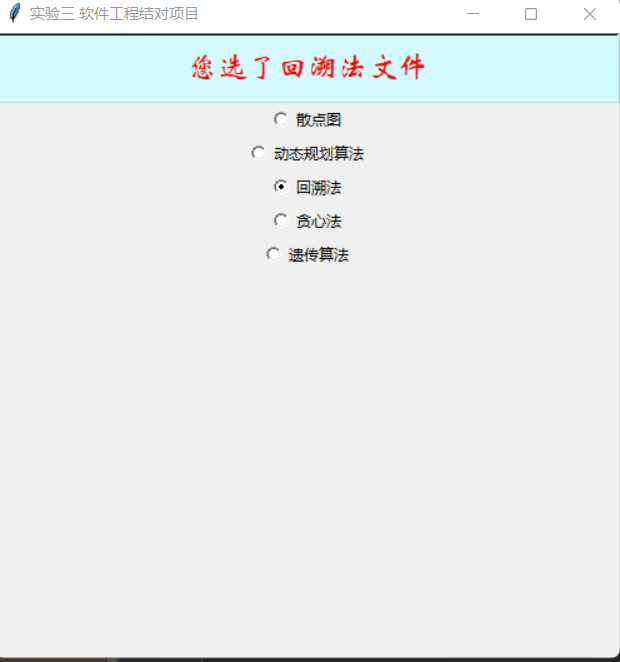

散点图绘制
psp
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 10 | 18 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 8 | 12 |
| Development | 开发 | 300 | 380 |
| Analysis | 需求分析(包括学习新技术) | 30 | 45 |
| Design Spec | 生成设计文档 | 15 | 25 |
| Design Review | 设计复审(和同事审核设计文档) | 15 | 24 |
| Coding Standard | 代码规范(为目前的开发制定合适的规范) | 10 | 18 |
| Design | 具体设计 | 120 | 160 |
| Coding | 具体编码 | 40 | 80 |
| Code Review | 代码复审 | 30 | 40 |
| Test | 测试(自我测试,修改代码, 提交修改) | 30 | 38 |
| Reporting | 报告 | 48 | 65 |
| Test Report | 测试报告 | 20 | 24 |
| Size Measurement | 计算工作量 | 16 | 24 |
| Postmortem & Process Improvement Plan | 事后总结,并提出过程改进计划 | 12 | 15 |
结对讨论照片
实验总结:
通过此次实验结对编程来设计实例数据集算法实验平台,在设计过程之中理解和学习了代码的风格规范和设计规范,同时也对复审的含义和形式有了一定的理解,通过结对编程深刻体会到了两人合作带来的效果,在软件的开发与设计之中,两人相互交换意见以及相互合作大大提高了编写的速率,降低了在编写过程出现错误的概率。同时也可以更加容易的在测试过程之中发现问题的所在。但是因部分知识的缺乏导致此次任务完成的不是很好。


