201971010118-梁春云 实验二 个人项目《0-1背包问题》
| 项目 | 内容 |
|---|---|
| 课程班级博客 | [https://edu.cnblogs.com/campus/xbsf/2019nwnucs] |
| 作业要求链接 | [https://edu.cnblogs.com/campus/xbsf/2019nwnucs/homework/12527] |
| 课程学习目标 | (1)掌握软件项目个人开发流程。(2)掌握Github发布软件项目的操作方法。 |
| 对学习目标的帮助 | (1)了解了个人软件项目开发流程 (2)学会在Gitub上发布软件项目 |
| 项目Github的地址 | [https://github.com/liangchunyun/b1] |
- 任务一 阅读教师博客“常用源代码管理工具与开发工具”内容要求,点评班级博客。
| 评论链接 | 评论内容 |
|---|---|
| [https://www.cnblogs.com/bkbkb/p/15977654.html] | 排版整洁、清晰,对于提出的问题也进行了非常详细的阐述和引用,对于第三问题以表格的形式更加清楚给出计算机科学与软件工程不同侧重点,值得学习。 |
| [https://www.cnblogs.com/yingyaoyao/p/15967395.html] | 博文格式编排整洁、清晰,在提出的问题上加上了对课本内容引用,能够更加清楚了解作者的问题。 |
| [https://www.cnblogs.com/byg-zyy/p/15954328.html] | 博客格式编排整齐,特别是在一些问题上以不同颜色标记出来,让阅读者看的更加清晰。对于问题的提出以及阐述上是非常的详细,此博客提出的问题是我之前有所忽略,对我有很高的学习价值,在以后学习过程我会注意这些问题。 |
-
任务二 总结详细阅读《构建之法》第1章、第2章,掌握PSP流程。
- 1.第一章总结
-
这一章主要讲了计算机科学的领域、软件的特性、软件工程、软件工程与计算机科学的关系。软件=程序+软件工程,软件工程是把系统的、有序的、可量化的方法应用到软件的开发、运营和维护上的过程,软件工程的核心部分是构建管理、源代码管理、软件设计、软件测试、项目管理。
-
软件的特性:(1)复杂性 (2)不可见性 (3)易变形 (4)服从性 (5)非连续性
-
软件工程与计算机科学的侧重点
计算机科学 软件工程 发展和研究长期的、客观的真理 短期的实际结果 理想化的 对各种因素的折衷 确定性,完美,通用性 对不确定性和风险的管理,足够好,具体的应用 各个学科独立深入研究,做出成果 关注和应用各个相关学科的知识,解决问题 理论统一 百花齐放的实践方法 强调原创性 最好的、成熟的实践方法 形式化,追求简明的公式 在实践中建立起来的灵感和直觉 正确性 可靠性
-
- 2.第二章总结
- 主要讲解个人技术和流程,因为团队需要一定的流程来管理开发活动,每个工程师在软件生命周期所做的工作也应该有一个流程,这一章中着重介绍PSP,即个人软件开发流程。卡内基梅隆大学的能力成熟度模型(CMM和CMMI),是用来衡量一个团队能力的一套模型。CMU的专家们针对软件工程师也有一套模型,叫 Personal Software Process(PSP)。
- 3.PSP流程
- psp是一种可用于控制、管理和改进个人工作方式的自我持续改进过程,是一个包括软件开发表格、指南和规程的结构化框架。PSP与具体的技术(程序设计语言、工具或者设计方法)相对独立,其原则能够应用到几乎任何的软件工程任务之中。PSP能够说明个体软件过程的原则; 帮助软件工程师作出准确的计划;确定软件工程师为改善产品质量要采取的步骤;建立度量个体软件过程改善的基准;确定过程的改变对软件工程师能力的影响。
- psp具有的特点:(1)不局限于某一种软件技术(如编程语言),而是着眼于软件开发的流程,这样,开发不同应用的软件工程师可以互相比较。(2)不依赖于考试,而主要靠工程师自己收集数据,然后分析,提高。(3)在小型、初创的团队中,很难找到高质量的项目需求,这意味着给程序员的输入质量不高。在这种情况下,程序员的输出(程序/软件)往往质量也不高,然而这并不能全部由程序员负责。(4)PSP依赖于数据,需要工程师输入数据,记录工程师的各项活动,这本身就需要不小的时间代价。(5)PSP的目的是记录工程师如何实现需求的效率,而不是记录顾客对产品的满意度。
- 1.第一章总结
-
任务三 项目开发背景
- 1.需求分析
背包问题是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式。具体的描述:{0-1}背包问题是从若干具有价值系数与重量系数的物品之中,选择若干物品装入有重量限制的背包之中,使其装入的物品在重量之和不超过背包载重前提之下价值系数达到最大。 - 2.功能设计
- 基本功能
1.可正确读入实验数据文件的有效{0-1}KP数据;
2.能够绘制任意一组{0-1}KP数据以价值重量为横轴、价值为纵轴的数据散点图;
3.能够对一组{0-1}KP数据按重量比进行非递增排序;
4.用户能够自主选择贪心算法、动态规划算法、回溯算法求解指定{0-1} KP数据的最优解和求解时间(以秒为单位);
5.任意一组{0-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出EXCEL文件。
- 基本功能
- 3.设计实现
- 动态规划法
思想:将待求解的问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。
步骤:(1)找出最优解的性质,刻画出结构特征
(2)递归的定义最优解的值
(3)自底向上的方式计算最优值(例如0/1背包问题将价值从低到高排序,再依次像背包中放入,调整)
(4)根据最优值构造最优解(求出哪些物品放在了背包中,标记为1,否则标记为0) - 回溯法
思想:设n件物品重量分别为w1,w2,…,wn的物品,用数组w[1 … n]存放,物品的价值分别为v1,v2,…,vn,用数组v[n]存放;限制重量用W表示。用x[1 … n]数组存放最优解,其中每个元素取1或0,x[i]=1表示第i个物品放入背包中,x[i]=0表示第i个物品不放入背包中。最优解问题,显然其解空间是子集树(每个物品要么装入,要么不装入),每个结点表示背包的一种选择状态,记录当前放入背包的物品总重量和总价值,每个分枝结点下面有两条边表示对某物品是否放入背包的两种可能选择。
- 动态规划法
- 1.需求分析
点击查看代码
int KnapSack2(int n,goods a[],int C,int x[])
{
int i,j;
int V[N][10*N];
for(int i=0;i<=n;i++) //初始化第0列
V[i][0]=0;
for(int j=0;j<=C;j++) //初始化第0行
V[0][j]=0;
for(int i=1;i<=n;i++) //计算第i行,进行第i次迭代
for(int j=1;j<=C;j++)
if(j<a[i-1].w)
V[i][j]=V[i-1][j];
else
V[i][j]=max(V[i-1][j],V[i-1][j-a[i-1].w]+a[i-1].p);
j=C; //求装入背包的物品
for (int i=n;i>0;i--)
{
if (V[i][j]>V[i-1][j]){
x[i-1]=1;
j=j-a[i-1].w;
}
else x[i-1]=0;
}
return V[n][C]; //返回背包取得的最大价值
}
点击查看代码
int BackTrack(int i)
{
if(i>n-1){
if(bestP<cp){
for (int k=0;k<n;k++) X[k]=cx[k];//存储最优路径
bestP=cp;
}
return bestP;
}
if(cw+a[i].w<=C){ //进入左子树
cw=cw+a[i].w;
cp=cp+a[i].p;
cx[a[i].sign]=1; //装入背包
BackTrack(i+1);
cw=cw-a[i].w;
cp=cp-a[i].p; //回溯,进入右子树
}
cx[a[i].sign]=0; //不装入背包
BackTrack(i+1);
return bestP;
}
-
测试运行
(1)结果截图
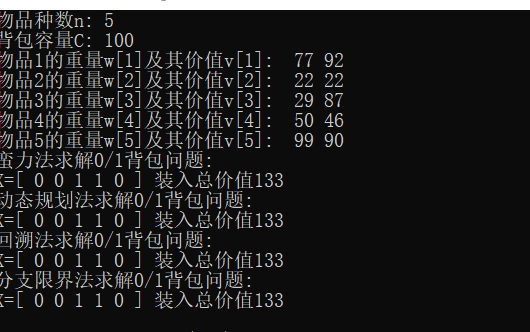
(2) 结果截图
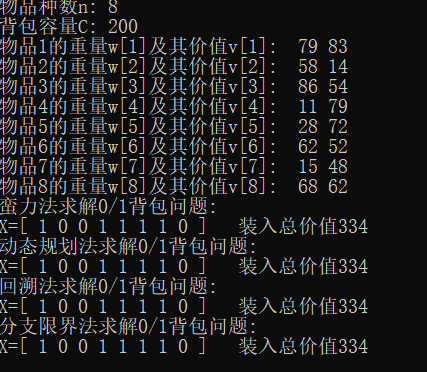
-
PSP展示
| PSP2.1 | 任务内容 | 计划共完成需要的时间(min) | 实际完成需要的时间(min) |
|---|---|---|---|
| Planning | 计划 | 10 | 8 |
| Estimate | 估计这个任务需要多少时间,并规划大致工作步骤 | 15 | 12 |
| Development | 开发 | 220 | 275 |
| Analysis | 需求分析(包括学习新技术) | 35 | 45 |
| Design Spec | 生成设计文档 | 17 | 19 |
| Design Review | 设计复审(和同事审核设计文档) | 10 | 20 |
| Coding Standard | 代码规范(为目前的开发制定合适的规范) | 15 | 28 |
| Design | 具体设计 | 50 | 110 |
| Coding | 具体编码 | 60 | 70 |
| Code Review | 代码复审 | 30 | 35 |
| Test | 测试(自我测试,修改代码, 提交修改) | 20 | 22 |
| Reporting | 报告 | 40 | 35 |
| Test Report | 测试报告 | 15 | 12 |
| Size Measurement | 计算工作量 | 10 | 18 |
| Postmortem & Process Improvement Plan | 事后总结,并提出过程改进计划 | 12 | 20 |
-
总结
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1 }Knapsack Problem,{0-1}KP)是最基本的KP问题形式,在本次实验之中未能通过正确读入数据文件中有效D{0-1}KP数据,主要是通过键盘输入获取相应的数据。但在此次实验之中,体会到了软件设计的模块化原则,具体的体现如下:- 进行项目需求分析
- 功能设计
- 设计实现
- 测试运行
-
任务四 将项目源码的完整工程文件提交到你注册Github账号的项目仓库中



