P4423 题解

前言

题目传送门！

更好的阅读体验？

刚学分治就来写篇题解纪念一下，其实和平面最近点对一样的（总共四倍经验！）。

思路

根据 P7883 的分治思路，这题我们可以考虑用相似的方法解决。

首先将点集按 \(x\) 坐标从小到大排序。然后分治。

对于 \(\left[l, r\right]\) 区间，分治为 \(\left[l, mid\right]\) 与 \(\left[mid+1, r\right]\) 两个区间解决。

容易发现，答案只有以下三种可能：

1. 由左端三个点构成的三角形。
2. 由右端三个点构成的三角形。
3. 左右端加起来取够三个点，构成的三角形。

根据分治的思想，前两类我们已经解决了，于是我们看第三类。

找到 \(x\) 轴意义上中间的那条直线，它就是划分线。

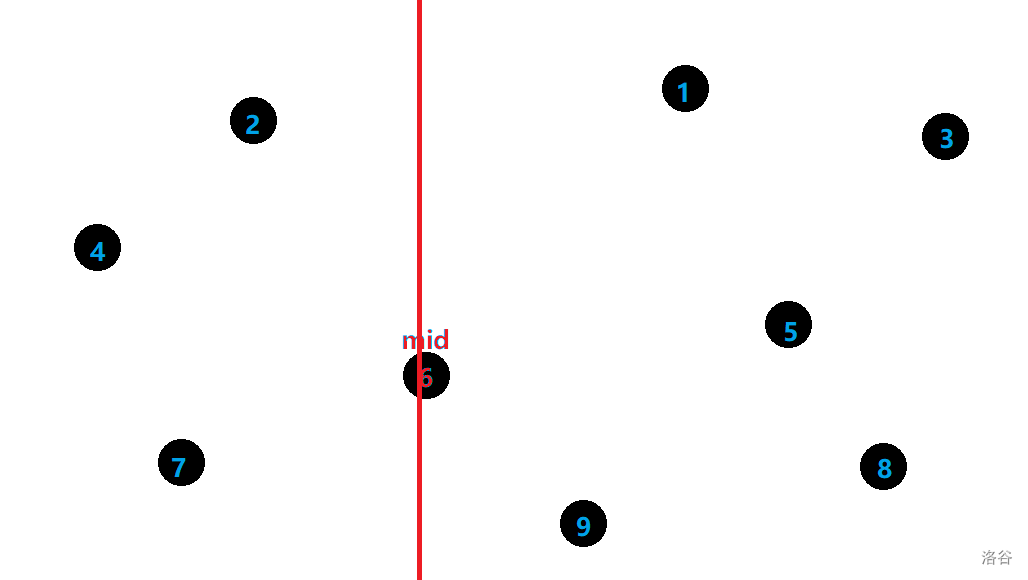
考虑一个常见的性质：对于三角形上的一条边 \(w\)，若其周长 \(C \ge k\)，则 \(w < \dfrac{k}{2}\)。原因比较显然就不证了。

应用到这题，设左右两边构成的答案为 \(ans\)，则三角形合法，当且仅当

\[\begin{cases} \mid X_{a,b,c} - X_{mid}\mid < \dfrac{ans}{2} \\ Y_a - Y_b < \dfrac{ans}{2} \\ Y_b - Y_c < \dfrac{ans}{2} \\ Y_c - Y_a < \dfrac{ans}{2} \end{cases} \]

此处 \(Y\) 有关的运算不用加绝对值的原因是，我们按照 \(y\) 坐标排序了，换句话说点对是有序的，这样既方便又不会重复枚举。

这样就有一个简明的做法，我们划出中线，筛选出所有 \(\mid X_u - X_{mid}\mid < \dfrac{ans}{2}\) 的点。

这些点还需要满足 \(y\) 坐标的限制，这个在枚举的时候限制一下就行了。

	vector <Node> tmp;
	for (int i = l; i <= r; i++)
		if (abs(a[i].x - a[mid].x) < ans / 2) //距离中线的距离符合要求
			tmp.push_back(a[i]);
	sort(tmp.begin(), tmp.end(), cmpy);
	
	int siz = tmp.size();
	for (int i = 0; i < siz; i++) //枚举三个符号要求的点
		for (int j = i + 1; j < siz && tmp[j].y - tmp[i].y < ans / 2; j++)
			for (int k = j + 1; k < siz && tmp[k].y - tmp[i].y < ans / 2; k++)
				ans = min(ans, dis(tmp[i], tmp[j]) + dis(tmp[j], tmp[k]) + dis(tmp[k], tmp[i]));

正解还是暴力？

现在有了一个问题：如果全部点都距离非常近，那么会不会使得三重循环寄爆炸，变成 \(O(n^3)\) 级别呢？

这个问题非常重要。我们回想一下平面最近点对的做法：

对于一个点，能与它组成点对的（此处点对是有序的）点必须满足 \(\mid X_u-X_{mid}\mid\)，\(\mid X_v-X_{mid}\mid\) 与 \(Y_v-Y_u\) 都小于 \(ans\)，所以符合要求的点一定在下图框框内部。

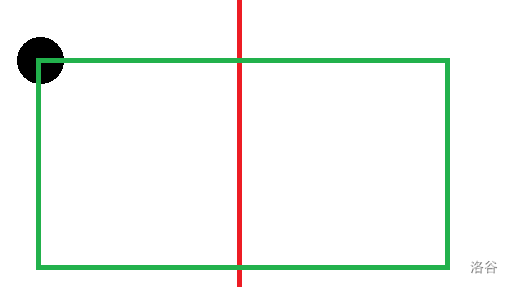
把长方形划分成八个边长为 \(\dfrac d2\) 的小正方形。每个正方形的对角线长度是

\[\sqrt{2\cdot(\dfrac d2)^2}=\sqrt{\dfrac{d^2}2} =\dfrac d{\sqrt2}<d \]

换句话说，同一个正方形里面不能有两个点，否则 \(ans\) 就不是最小距离了。那么总共可以选 \(2^2\times2=8\) 个点。

---

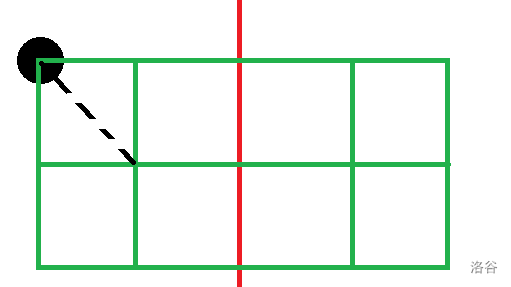
回到这个问题。考虑划分成九个边长为 \(\dfrac d3\) 的小正方形。

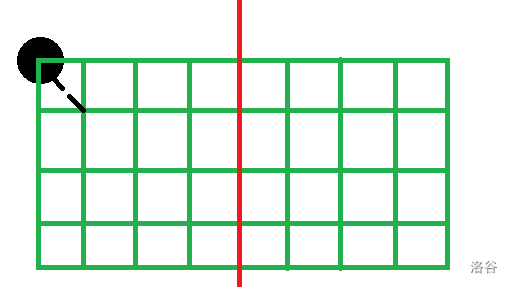
同样地，计算它的对角线：

\[\sqrt{2\cdot(\dfrac d4)^2}=\sqrt{\dfrac{d^2}8}=\dfrac d{2\sqrt2}<\dfrac d2 \]

换句话说，同一个正方形里面不能有两个点，否则 \(ans\) 就不是最小距离了。那么总共可以选 \(4^2\times2=32\) 个点。

时间复杂度就自然正确了，并且由于这种是极端情况，实际跑得快非常多。

代码

我写了两个版本，前者是 \(O(n \log^2 n)\) 的递归内 sort() 版本，后者是递归内线性归并的 \(O(n\log n)\) 分治。

本质都是相同的，方便大家对拍吧。

\(O(n \log^2 n)\) 的版本：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;

typedef pair <int, int> pii;
#define x first
#define y second
bool cmpx(pii p, pii q) {return p.x < q.x;}
bool cmpy(pii p, pii q) {return p.y < q.y;}

const int N = 2e5 + 5;
pii a[N];
double dis(pii p, pii q) {return sqrt(1ll * (p.x - q.x) * (p.x - q.x) + 1ll * (p.y - q.y) * (p.y - q.y));}
double solve(int l, int r)
{
	if (l >= r) return 1e9;
	int mid = (l + r) >> 1;
	double ans = min(solve(l, mid), solve(mid + 1, r));
	
	vector <pii> tmp;
	for (int i = l; i <= r; i++)
		if (abs(a[i].x - a[mid].x) < ans / 2) //距离中线的距离符合要求
			tmp.push_back(a[i]);
	sort(tmp.begin(), tmp.end(), cmpy);
	
	int siz = tmp.size();
	for (int i = 0; i < siz; i++) //枚举三个符号要求的点
		for (int j = i + 1; j < siz && tmp[j].y - tmp[i].y < ans / 2; j++)
			for (int k = j + 1; k < siz && tmp[k].y - tmp[i].y < ans / 2; k++)
				ans = min(ans, dis(tmp[i], tmp[j]) + dis(tmp[j], tmp[k]) + dis(tmp[k], tmp[i]));
	return ans;
}
int main()
{
	int n;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].x, &a[i].y);
	sort(a + 1, a + n + 1, cmpx);
	printf("%.6lf", solve(1, n));
	return 0;
}

\(O(n \log n)\) 的版本：

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;

typedef pair <int, int> pii;
#define x first
#define y second
bool cmpx(pii p, pii q) {return p.x < q.x;}
bool cmpy(pii p, pii q) {return p.y < q.y;}

const int N = 2e5 + 5;
pii a[N];
double dis(pii p, pii q) {return sqrt(1ll * (p.x - q.x) * (p.x - q.x) + 1ll * (p.y - q.y) * (p.y - q.y));}
pii t[N]; int cur;
void merge(int l, int r) //将 [l,mid] 与 [mid+1,r] 合并，原因是两部分已经是有序的了
{
	int mid = (l + r) >> 1, i = l, j = mid + 1; cur = l;
	while (i <= mid && j <= r)
		if (a[i].y < a[j].y) t[cur++] = a[i++];
		else t[cur++] = a[j++];
	while (i <= mid) t[cur++] = a[i++];
	while (j <= r) t[cur++] = a[j++];
	for (int k = l; k <= r; k++) a[k] = t[k];
}
double solve(int l, int r)
{
	if (l >= r) return 1e9;
	int mid = (l + r) >> 1, midval = a[mid].x; //注意此处一定要先存下来 midval，否则 merge() 会改变
	double ans = min(solve(l, mid), solve(mid + 1, r));
	merge(l, r);
	
	vector <pii> tmp;
	for (int i = l; i <= r; i++)
		if (abs(a[i].x - midval) < ans)
			tmp.push_back(a[i]);
	//sort(tmp.begin(), tmp.end(), cmpy); //这样就不用排序了qwq
	
	int siz = tmp.size();
	for (int i = 0; i < siz; i++) //枚举三个合法点
		for (int j = i + 1; j < siz && tmp[j].y - tmp[i].y < ans / 2; j++)
			for (int k = j + 1; k < siz && tmp[k].y - tmp[i].y < ans / 2; k++)
				ans = min(ans, dis(tmp[i], tmp[j]) + dis(tmp[j], tmp[k]) + dis(tmp[k], tmp[i]));
	return ans;
}
int main()
{
	int n;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].x, &a[i].y);
	sort(a + 1, a + n + 1, cmpx);
	printf("%.6lf", solve(1, n));
	return 0;
}

希望能帮助到大家！