CF1696E 题解
前言
结论题。
思路
很明显这是计数题而不是最小值。手玩样例。
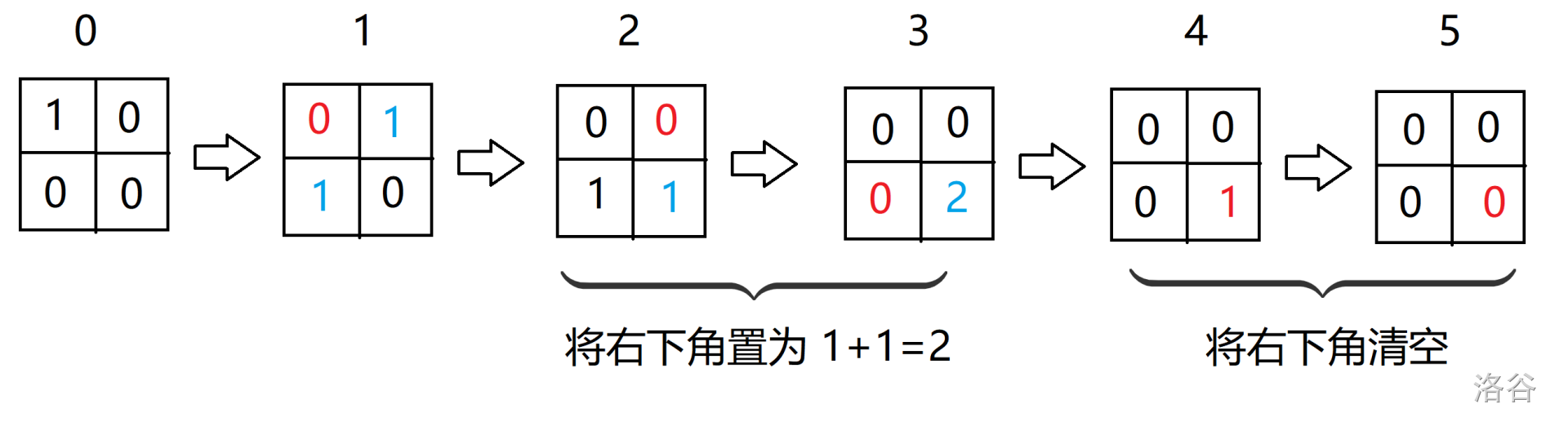
很容易发现以下性质:
- 第一步肯定是操作 \((1, 1)\)。
- 上边缘与左边缘(也就是 \((1, x)\) 与 \((x, 1)\) 的点)操作次数必为 \(1\)。
- 对于一个元素,如果上方的值为 \(x\),左方的值为 \(y\),操作 \((x + y)\) 次后,自己就会变成 \((x + y)\)。
- 对于右下角,若值为 \(x\),操作 \(x\) 次后清空,操作结束。
转化成数学语言,设 \((x, y)\) 号格子的值为 \(v_{x, y}\)(此处 \(x\) 是行,\(y\) 是列),则有:
\[v_{x, y} =
\begin{cases}
1 & x=1 \operatorname{or} y=1 \\
v_{x-1,y}+v_{x,y-1} & \text{otherwise}
\end{cases}
\]
画出来,斜着看,发现就是杨辉三角。众所周知杨辉三角的每一项都可以对应 \(C(n, m)\),画一个图方便理解。
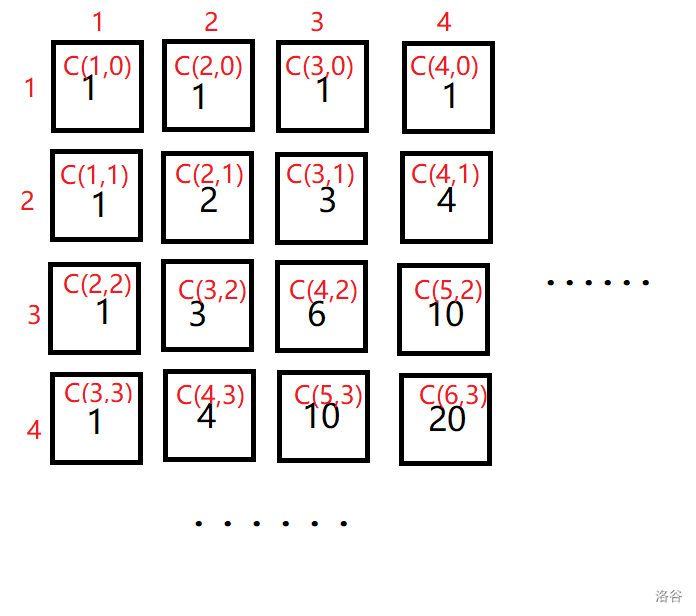
容易发现 \(v_{x,y} = C(x+y-2, x-1)\)(第一行貌似不属于这个规律)。
综上所述,
\[\begin{aligned}
\text{answer}
& = a_1 + \sum\limits_{i=2}^{n+1}\sum\limits_{j=1}^{a_i} v_{i,j} \\
& = a_1 + \sum\limits_{i=2}^{n+1}\sum\limits_{j=1}^{a_i} C(i+j-2, i-1) \\
& = a_1 + \sum\limits_{i=2}^{n+1}\sum\limits_{j=1}^{a_i}\Big(C(i+j-1,i)-C(i+j-2,i)\Big) \\
& = a_1 + \sum\limits_{i=2}^{n+1}\Big(C(i,i)-C(i-1,i)+C(i+1,i)-C(i,i)+\cdots+C(i+a_i-1,i)-C(i+a_i-2,i)\Big) \\
& = a_1 + \sum\limits_{i=2}^{n+1} C(i+a_i-1,i)-C(i-1,i) \\
& = a_1 + \sum\limits_{i=2}^{n+1} C(i+a_i-1,i) \\
& = \sum\limits_{i=1}^{n+1} C(i+a_i-1,i)
\end{aligned}
\]
其中,第二步到第三步是使用 \(C(x,y)=C(x-1,y-1)+C(x-1,y)\) 变形成 \(C(x-1,y-1)=C(x,y)-C(x-1,y)\) 得到的。
于是预处理一下组合数就做完了。
代码
希望能帮助到大家!

