P4012 题解
前言
网络流 \(24\) 题:最大费用最大流。
快捷步骤
这里先说两点。第一点,很多题解提到了,类似于把图翻过来的操作。
这实际上是完全没必要的。你把全部点翻了和没翻一样,为啥要翻。而且翻了也不会让你理解起来更顺畅。
第二点,实际上,没必要费心思给每一个点编号。你直接用 idx 记录下全部点即可。
这也是非常显然的事情。
s = ++idx, t = ++idx;
for (int i = 0; i <= n; i++)
for (int j = 0; j <= m; j++)
id[i][j] = ++idx; //给每个点一个编号
思路
首先我们只看每一个点。是典型的方格取数问题,可以考虑费用流。
对于一个相邻的、可以走到的点 \((x, y)\) 与 \((dx, dy)\),我们可以直接连边 \((x,y) \xrightarrow{cap=1\ cost=w} (dx,dy)\),表示:你想拿到这个格子的价值,那么你只能拿一次。
但是这样并不对。因为只是这样子,代表这一条边只能走一次。很显然这是不对的,因为你可以走这条边,但是什么都不拿。
于是我们再建一条 \((x,y) \xrightarrow{cap=\infty \ cost=0} (dx,dy)\),表示:这条边随便走,但是没有费用。
这就是第一步。我们再看一下源点与汇点:那 \(a\) 个点就是源点,那 \(b\) 个点就是汇点。
很套路地,建立多源多汇即可:超级源点连向每一个源点,超级汇点连向每一个汇点。
具体地:
- 假设有 \(k\) 个深海机器人从 \((x, y)\) 位置出发,就 \(S \xrightarrow{cap=k \ cost=0} (x, y)\)。
- 假设有 \(r\) 个深海机器人从 \((x, y)\) 位置作为目的地,就 \((x,y) \xrightarrow{cap=k \ cost=0} T\)。
于是这题就做完了。您也可以尝试看看下面这张图:
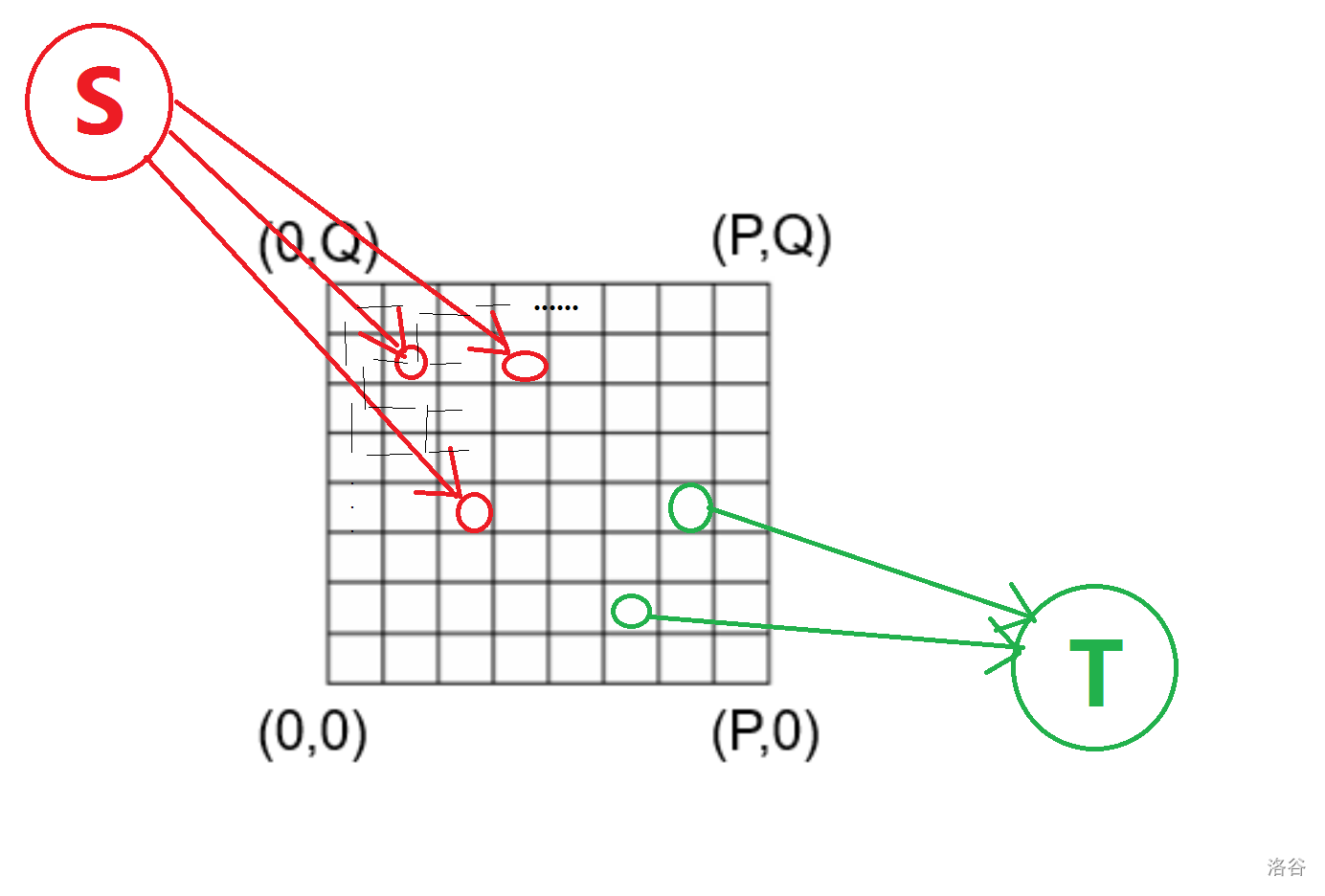
代码
最多的点数应该是 \(nm\) 的级别(还要多一些),可以直接按 \(400\) 算。
最多的边数大概是 \(2 \times (2nm + 2nm + a + b) = 8nm+2a+2b \approx 8\times400+2\times10+2\times10=3240\)(反正开多一点准没错)。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
/**********最大费用最大流模版,可以自己写**********/
const int N = 400, inf = 0x3f3f3f3f;
struct Edge {int now, nxt, w, cost;} e[3240];
int head[N], cur = 1;
void ad(int u, int v, int w, int cost)
{
e[++cur].now = v, e[cur].nxt = head[u], e[cur].w = w, e[cur].cost = cost;
head[u] = cur;
}
void add(int u, int v, int w, int cost) {ad(u, v, w, cost), ad(v, u, 0, -cost);}
int dis[N], icost[N], pre[N]; bool inque[N];
int s, t;
bool spfa()
{
queue <int> q;
memset(dis, -0x3f, sizeof dis), memset(icost, 0, sizeof icost);
q.push(s), dis[s] = 0, icost[s] = inf, inque[s] = true;
while (!q.empty())
{
int u = q.front();
q.pop(), inque[u] = false;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].now;
if (!e[i].w) continue;
if (dis[u] + e[i].cost > dis[v])
{
dis[v] = dis[u] + e[i].cost, pre[v] = i;
icost[v] = min(icost[u], e[i].w);
if (!inque[v]) q.push(v), inque[v] = true;
}
}
}
return icost[t] > 0;
}
int EK()
{
int ans = 0;
while (spfa())
{
int w = icost[t];
ans += w * dis[t];
for (int i = t; i != s; i = e[pre[i] ^ 1].now)
e[pre[i]].w -= w, e[pre[i] ^ 1].w += w;
}
return ans;
}
/**********最大费用最大流模版,可以自己写**********/
int id[20][20];
int main()
{
int a, b, n, m, idx = 0;
scanf("%d%d%d%d", &a, &b, &n, &m);
s = ++idx, t = ++idx;
for (int i = 0; i <= n; i++)
for (int j = 0; j <= m; j++)
id[i][j] = ++idx; //给每个点编号
for (int i = 0; i <= n; i++)
for (int j = 0; j < m; j++)
{
int w;
scanf("%d", &w);
add(id[i][j], id[i][j + 1], 1, w), add(id[i][j], id[i][j + 1], inf, 0); //建立相邻点的边
}
for (int j = 0; j <= m; j++)
for (int i = 0; i < n; i++)
{
int w;
scanf("%d", &w);
add(id[i][j], id[i + 1][j], 1, w), add(id[i][j], id[i + 1][j], inf, 0); //建立相邻点的边
}
while (a--) //建立超级源点与多个源点的边
{
int w, i, j;
scanf("%d%d%d", &w, &i, &j);
add(s, id[i][j], w, 0);
}
while (b--) //建立超级汇点与多个汇点的边
{
int w, i, j;
scanf("%d%d%d", &w, &i, &j);
add(id[i][j], t, w, 0);
}
cout << EK();
return 0;
}
希望能帮助到大家!

