CF1537D 题解

前言

题目传送门！

更好的阅读体验？

遇到这种博弈论的题目，当然是要打表找规律了！

思路

首先，很容易想到暴力递推。

代码在上方的链接里。然后看几眼就能发现，在大部分情况下，如果 \(n\) 是偶数那么 Alice 获胜，否则 Bob 获胜。

再多看几眼，会发现：有些地方 \(n\) 是偶数，但是仍然是 Bob 获胜！

于是，我们再打表，单独看这些地方。然后就会发现：

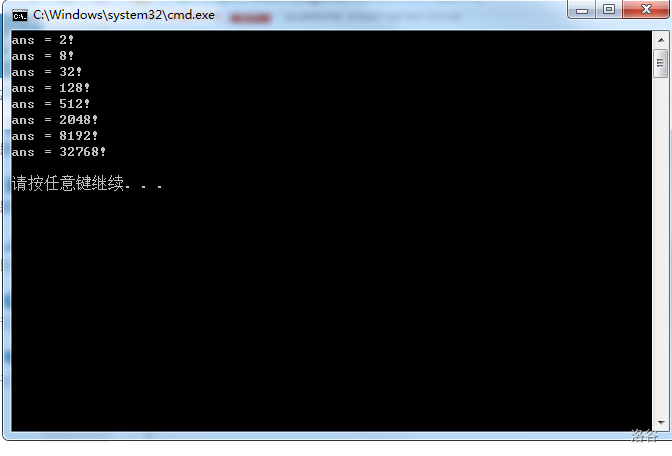
这些数有什么特点呢？很容易想到，\(2 = 2^1\)，\(8 = 2^3\)，\(32 = 2^5\)，\(128 = 2^7\)，以此类推。

换句话说，只要 \(n = 2^{k}\)（\(k\) 是奇数），那么这种情况就是特例，是 Bob 获胜。

然后写成代码就行。

代码

代码内有一个 map，里面存储的是上述的特殊值。这个也是可以打表的。

#include <iostream>
#include <cstdio>
#include <map>
using namespace std;
map <int, bool> zlt;
bool solve()
{
	int n;
	scanf("%d", &n);
	if (zlt[n]) return false; //可以理解为特判
	return (n % 2 == 0); //奇数就是Bob，偶数就是Alice
}
int main()
{
	zlt[2] = zlt[8] = zlt[32] = zlt[128] = zlt[512] = zlt[2048] = zlt[8192] = zlt[32768] = zlt[131072] = zlt[524288] = zlt[2097152] = zlt[8388608] = zlt[33554432] = zlt[134217728] = zlt[536870912] = true;
	ios::sync_with_stdio(false);
	int T;
	scanf("%d", &T);
	while (T--)
		if (solve()) puts("Alice");
		else puts("Bob");
	return 0;
}

希望能帮助到大家！