UVA1331 题解

前言

题目传送门！

更好的阅读体验？

第一次写黑题题解 。

计算几何、区间 $\text{DP}$。

思路

我们可以把大多边形分拆成小的多边形来看，并且小的多边形的顶点，在大多边形的顶点的编号是连续的。

所以考虑区间 $\text{DP}$。设 $d{p}_{i,j}$ 表示用 $[i,j]$ 之间的所有格点组成的小多边形，怎样能使答案最小。

最终结果显然就是 $d{p}_{1,n}$。

考虑如何转移。对于 $d{p}_{i,j}$，找一个断点将这个多边形一分为二，并取三个区域的答案最大值。

简单的说，转移方程就是：$d{p}_{i,j}=\underset{l<k<r}{min}\{max\{d{p}_{i,k},d{p}_{k,j},S\mathrm{△}{a}_i{a}_k{a}_j\}\}$。

求 $S\mathrm{△}{a}_i{a}_k{a}_j$，可以用叉积或者海伦公式算。

但是请注意，并不是所有 $k$ 都能转移的，所以这样写不完全正确。

比如说下图的情况就是不合法的转移：

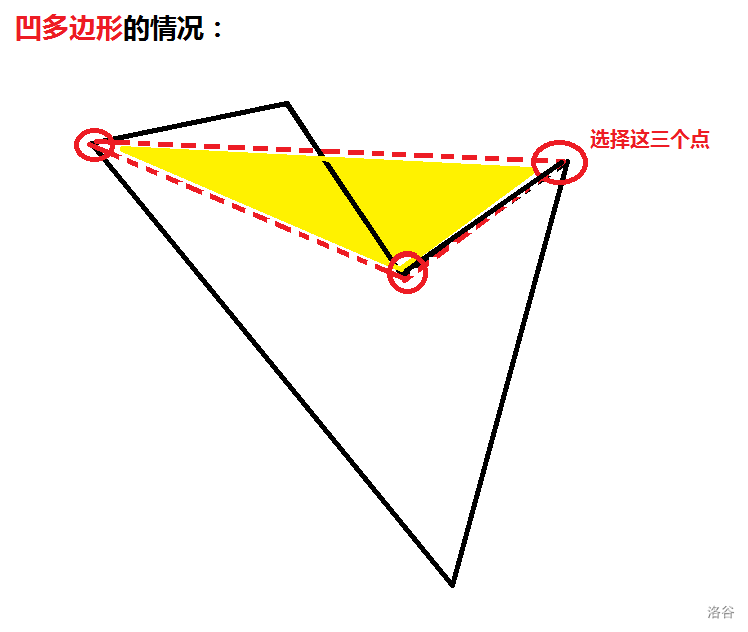
显然，三角形超出了多边形的位置。因此，我们要判断这个三角形是否在多边形内。

也就是说，大多边形的每个点（除了三角形的这三个点）都不能在三角形内部。

这一点还是比较好判断的：如果 $S\mathrm{△}{a}_x{a}_j{a}_k+S\mathrm{△}{a}_i{a}_x{a}_k+S\mathrm{△}{a}_i{a}_j{a}_x=S\mathrm{△}{a}_i{a}_j{a}_k$，说明 $x$ 点在 $\mathrm{△}{a}_i{a}_j{a}_k$ 内。

这个公式是什么意思呢？举例来说，合法情况就是下图：

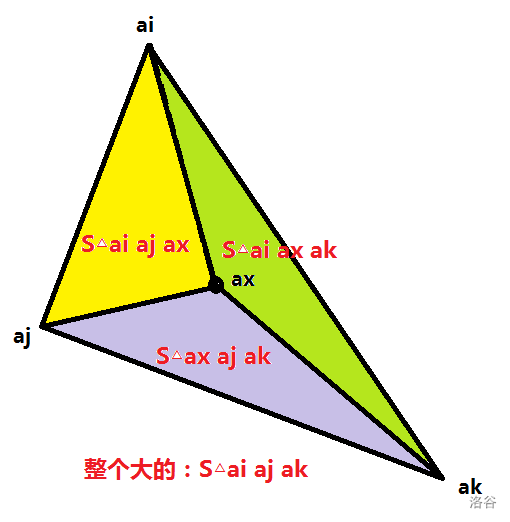
那么这题就完美做完啦！

完整代码

本题精度诡异，我的代码 ${10}^{-8}$ 与 ${10}^{-9}$ 都过不了，但是设成 ${10}^{-5}$ 可以过。

#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstring>
using namespace std;

typedef double db;
typedef pair <int, int> pii;
#define x first
#define y second
const int N = 55;

int n;
pii a[N];
namespace calc {
    db dis(int i, int j) //a[i] 到 a[j] 的距离
    {
        db dx = a[i].x - a[j].x, dy = a[i].y - a[j].y;
        return sqrt(dx * dx + dy * dy);
    }
    db area(int i, int j, int k) //三角形 a[i],a[j],a[k] 的面积
    {
        db a = dis(i, j), b = dis(i, k), c = dis(j, k);
        db s = (a + b + c) / 2;
        return sqrt(s * (s - a) * (s - b) * (s - c));
    }
    bool all_out_triangle(int a, int b, int c) //是否其余的全部点均在 三角形a[i],a[j],a[k] 外面
    {
        for (int i = 1; i <= n; i++)
            if (i != a && i != b && i != c)
            {
                db x = area(a, b, c);
                db y = area(a, b, i) + area(a, i, c) + area(i, b, c);
                if (fabs(x - y) < 1e-5) return false; //即：x不等于y。这样写是防止精度丢失
            }
        return true;
    }
};

db dp[N][N];
db MAX(db x, db y, db z) {return max(x, max(y, z));} //取 max(x, y, z)
void solve()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%d%d", &a[i].x, &a[i].y);

    memset(dp, 127, sizeof dp); //double 初始化要用 127 而不是 0x3f
    for (int i = 1; i < n; i++) dp[i][i + 1] = 0; //只有两个点
    for (int i = 1; i <= n - 2; i++) dp[i][i + 2] = calc::area(i, i + 1, i + 2); //有三个点，答案就是这个三角形的面积

    for (int len = 3; len <= n; len++) //区间 DP
        for (int i = 1, j = len; j <= n; i++, j++)
            for (int k = i + 1; k < j; k++)
                if (calc::all_out_triangle(i, j, k))
                    dp[i][j] = min(dp[i][j], MAX(dp[i][k], dp[k][j], calc::area(i, j, k)) );
    printf("%.1lf\n", dp[1][n]);
}
int main()
{
    ios::sync_with_stdio(false);
    int T;
    scanf("%d", &T);
    while (T--) solve();
    return 0;
}

希望能帮助到大家！