ABC277E 题解

前言

题目传送门！

更好的阅读体验？

非常套路的分层图，纪念赛时切掉了。

思路

我们以样例来解释。首先，这是最基础的图。

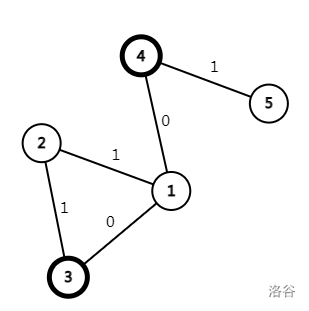
我们把图分成两层：第一层是原本 \(w = 1\) 的路可以通行，第二层是原本 \(w = 0\) 的路可以通行。

连接两层图的边，就是按钮所在的边。为什么呢？因为按一下按钮，边权就会全部取反，相当于跑到了不同的层上去。

也就是说，图会变成这个样子：

此时，边权就是真正的边权了：移动一步的代价为 \(1\)，所以同一层内，所有边的边权都是 \(1\)。

按按钮不需要代价，所以切换层的边的代价为 \(0\)。

然后跑最短路即可。答案就是这张图内的最短路。

由于边权只有 \(0\) 与 \(1\)，所以应该也可以跑 01-bfs，并且时间复杂度是 \(O(m)\)。

但是为了图方便，我就直接写了 Dijkstra 板子。

代码

省去了缺省源。个人认为还是打得很好看的！（自信）

const int N = 4e5 + 5; //开2倍
struct Edge {int now, nxt, w;} e[N << 1];
int head[N], cur;
void add(int u, int v, int w)
{
	e[++cur].now = v;
	e[cur].nxt = head[u];
	e[cur].w = w;
	head[u] = cur;
}
void ADD(int u, int v, int w) {add(u, v, w), add(v, u, w);}
 
struct Node {int pos, dis;};
bool operator <(Node y, Node x) {return x.dis < y.dis;}
 
int dis[N];
bool vis[N];
void dijkstra(int s) //完全是 Dijkstra 板子，你甚至可以复制板子的代码
{
	memset(dis, 0x3f, sizeof dis);
	priority_queue <Node> q;
	dis[s] = 0, q.push((Node){s, 0});
	while (!q.empty())
	{
		int u = q.top().pos;
		q.pop();
		if (vis[u]) continue;
		vis[u] = true;
		for (int i = head[u]; i; i = e[i].nxt)
		{
			int v = e[i].now;
			if (dis[u] + e[i].w < dis[v])
			{
				dis[v] = dis[u] + e[i].w;
				q.push((Node){v, dis[v]});
			}
		}
	}
}
void solve()
{
	int n, m, k;
	scanf("%d%d%d", &n, &m, &k);
	while (m--)
	{
		int u, v, w;
		scanf("%d%d%d", &u, &v, &w);
		if (w == 1) ADD(u, v, 1); //第一层
		else ADD(u + n, v + n, 1); //第二层
	}
	while (k--)
	{
		int u;
		scanf("%d", &u);
		ADD(u, u + n, 0); //切换层
	}
	dijkstra(1);
	//for (int i = 1; i <= (n << 1); i++) printf("from %d to %d is %d\n", 1, i, dis[i]);
	int t = min(dis[n], dis[n + n]);
	if (t == 0x3f3f3f3f) puts("-1");
	else cout << t << '\n';
}

希望能帮助到大家！