P4679 题解
前言
大力树剖!
做树剖时,大家可以膜拜 @liruiduan2 巨佬,他可以在考场上码 200 行的树剖题目。
思路
对于线段树的区间 \([l, r]\),记录三个东西:\(lmx_i\)、\(rmx_i\)、\(dis_{i, j}\)。
\(lmx_i\) (\(0 \le i \le 1\))表示从 \(l\) 的左或右节点出发,能走的最长距离。\(rmx_i\) 则是从 \(r\) 出发。
\(dis_{i, j}\)(\(0 \le i, j \le 1\))表示从 \(l\) 的左或右节点,走到 \(r\) 的左或右节点,最长距离。
合并操作看代码模拟就行,非常好理解。假设要把 \(x\) 与 \(y\) 合并到 \(ans\) 里:
ans.lmx[i] = max(ans.lmx[i], max(x.lmx[i], x.dis[i][j] + y.lmx[j]))ans.rmx[i] = max(ans.rmx[i], max(y.rmx[i], y.dis[j][i] + x.rmx[j]));- \(dis_{i, j}\) 用类似 floyd 的思想转移即可。
线段树是单点修改,不需要 pushdown,写起来非常舒服。
不过注意新建一个节点需要特殊处理。
inline void create(bool a[]) //创建一个新节点
{
int d = 2, x = a[0], y = a[1];
const int inf = 0x3f3f3f3f;
if (!x) d = x = -inf;
if (!y) d = y = -inf;
lmx[0] = rmx[0] = max(x, 0), lmx[1] = rmx[1] = max(y, 0);
dis[0][0] = x, dis[1][1] = y;
dis[0][1] = dis[1][0] = d;
}
所以接下来就是树剖了。前面是常规操作,最后可以得到两个点相遇后的两个结果。
但是这样做,求出的两个点的信息,是这样的:
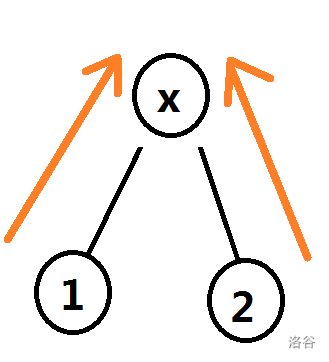
我们显然想让两个箭头是顺着的。
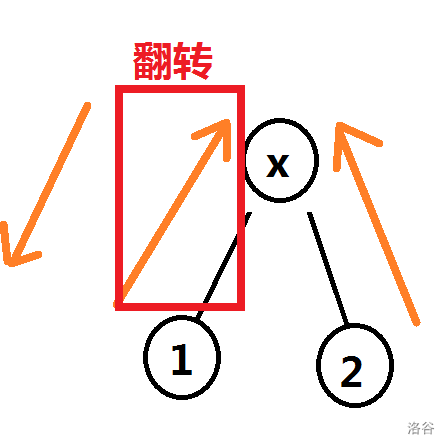
所以很简单,把一段翻转即可。这个时候再合并两段的答案就行了。
void Swap(Node &a) //把当前点翻转
{
for (int i = 0; i <= 1; i++) swap(a.lmx[i], a.rmx[i]);
swap(a.dis[0][1], a.dis[1][0]);
}
最后答案显然为 \(\max(lmx_{0}, lmx_{1})\)。
完整代码
有点长。可以用这份代码对拍。
/*树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖树剖*/
/*lrd爆切树剖lrd爆切树剖lrd爆切树剖lrd爆切树剖lrd爆切树剖lrd爆切树剖lrd爆切树剖lrd爆切树剖lrd爆切树剖*/
#include <iostream>
#include <cstdio>
#include <cstring>
#define space putchar(' ')
#define endl putchar('\n')
using namespace std;
typedef long long LL;
typedef unsigned long long ull;
typedef long double LD;
namespace io { //快读快写,可以直接忽略
void fastio()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
}
inline int read()
{
char op = getchar(); int x = 0, f = 1;
while (op < 48 || op > 57) {if (op == '-') f = -1; op = getchar();}
while (48 <= op && op <= 57) x = (x << 1) + (x << 3) + (op ^ 0x30), op = getchar();
return x * f;
}
inline void write(int x)
{
if (x < 0) putchar('-'), x = -x;
if (x > 9) write(x / 10);
putchar(x % 10 + 0x30);
}
} using namespace io;
const int N = 5e4 + 5;
struct Edge
{
int now, nxt;
} e[N << 1];
int head[N], cur;
inline void add(int u, int v) //链式前向星
{
e[++cur].now = v;
e[cur].nxt = head[u];
head[u] = cur;
}
int siz[N], wson[N], fa[N], dep[N];
void dfs(int u) //树剖两次 dfs
{
siz[u] = 1, dep[u] = dep[fa[u]] + 1;
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].now;
if (v != fa[u])
{
fa[v] = u;
dfs(v);
siz[u] += siz[v];
if (wson[u] == 0 || siz[v] > siz[wson[u]]) wson[u] = v;
}
}
}
int top[N];
bool map[N][2], zlt[N][2]; //zlt : 转化为dfn的地图
int dfn[N], vist;
void DFS(int u, int frt)
{
dfn[u] = ++vist;
top[u] = frt;
zlt[vist][0] = map[u][0], zlt[vist][1] = map[u][1];
if (wson[u] == 0) return;
DFS(wson[u], frt);
for (int i = head[u]; i; i = e[i].nxt)
{
int v = e[i].now;
if (v != fa[u] && v != wson[u]) DFS(v, v);
}
}
struct Node
{
int lmx[2], rmx[2], dis[2][2];
Node() {lmx[0] = lmx[1] = rmx[0] = rmx[1] = dis[0][0] = dis[0][1] = dis[1][0] = dis[1][1] = 0;}
inline void create(bool a[]) //创建一个新节点
{
int d = 2, x = a[0], y = a[1];
const int inf = 0x3f3f3f3f;
if (!x) d = x = -inf;
if (!y) d = y = -inf;
lmx[0] = rmx[0] = max(x, 0), lmx[1] = rmx[1] = max(y, 0);
dis[0][0] = x, dis[1][1] = y;
dis[0][1] = dis[1][0] = d;
}
} s[N << 2];
inline Node operator +(const Node &x, const Node &y) //合并两个节点
{
Node a;
for (int i = 0; i <= 1; i++)
for (int j = 0; j <= 1; j++)
{
a.lmx[i] = max(a.lmx[i], max(x.lmx[i], x.dis[i][j] + y.lmx[j]));
a.rmx[i] = max(a.rmx[i], max(y.rmx[i], y.dis[j][i] + x.rmx[j]));
a.dis[i][j] = -0x3f3f3f3f; //类似 floyd 的写法
for (int k = 0; k <= 1; k++) a.dis[i][j] = max(a.dis[i][j], x.dis[i][k] + y.dis[k][j]);
}
return a;
}
struct SegmentTree //线段树
{
inline int ls(int x) {return x << 1;}
inline int rs(int x) {return x << 1 | 1;}
inline void pushup(int pos) {s[pos] = s[ls(pos)] + s[rs(pos)];}
void build(int l, int r, int pos)
{
if (l == r) return s[pos].create(zlt[l]);
int mid = (l + r) >> 1;
build(l, mid, ls(pos));
build(mid + 1, r, rs(pos));
pushup(pos);
}
void update(int l, int r, int pos, int id, bool a[])
{
if (l == r) return s[pos].create(a);
int mid = (l + r) >> 1;
if (id <= mid) update(l, mid, ls(pos), id, a);
else update(mid + 1, r, rs(pos), id, a);
pushup(pos);
}
Node query(int l, int r, int pos, int L, int R) //warning: 由于空节点与非空节点合并会挂,所以要分开写
{
if (L <= l && r <= R) return s[pos];
int mid = (l + r) >> 1;
/*我平时的写法
Node ans;
if (L <= mid) ans = ans + query(l, mid, ls(pos), L, R);
if (mid < R) ans = ans + query(mid + 1, r, rs(pos), L, R);
return ans;
*/
if (L > mid) return query(mid + 1, r, rs(pos), L, R); //没有 L<=mid 说明有 mid<R
if (mid >= R) return query(l, mid, ls(pos), L, R); //没有 mid<R 说明有 L<=mid
return query(l, mid, ls(pos), L, R) + query(mid + 1, r, rs(pos), L, R); //两个非空节点合并才不会挂
}
} seg;
int n;
struct Tree //大力树剖!
{
void Swap(Node &a) //把当前点翻转
{
for (int i = 0; i <= 1; i++) swap(a.lmx[i], a.rmx[i]);
swap(a.dis[0][1], a.dis[1][0]);
}
int query(int x, int y)
{
Node nx, ny;
while (top[x] != top[y]) //下面注意要写成 nx = query + nx,因为空节点合并会有问题
{
if (dep[top[x]] > dep[top[y]])
nx = seg.query(1, n, 1, dfn[top[x]], dfn[x]) + nx, x = fa[top[x]];
else ny = seg.query(1, n, 1, dfn[top[y]], dfn[y]) + ny, y = fa[top[y]];
}
if (dep[x] > dep[y]) nx = seg.query(1, n, 1, dfn[y], dfn[x]) + nx;
else ny = seg.query(1, n, 1, dfn[x], dfn[y]) + ny;
Swap(nx);
Node ans = nx + ny;
return max(ans.lmx[0], ans.lmx[1]);
}
} tree;
int main()
{
n = read(); int T = read();
for (int i = 1; i < n; i++)
{
int u = read(), v = read();
add(u, v), add(v, u);
}
for (int i = 1; i <= n; i++)
{
char s[2]; scanf("%s", s);
map[i][0] = (s[0] == '.'), map[i][1] = (s[1] == '.');
}
dfs(1), DFS(1, 1);
seg.build(1, n, 1);
while (T--)
{
char op[2];
scanf("%s", op);
if (op[0] == 'C')
{
int i = read();
char s[2]; scanf("%s", s);
map[i][0] = (s[0] == '.'), map[i][1] = (s[1] == '.'); //暴力更新
seg.update(1, n, 1, dfn[i], map[i]);
}
else
{
int u = read(), v = read();
write(tree.query(u, v)), endl;
}
}
return 0;
}
/*
hack
5 1
4 5
2 5
4 3
4 1
..
#.
#.
#.
##
Q 2 4
*/
希望能帮助到大家!


