背包学习笔记

##前言

最近学习了背包，来写篇学习笔记。

如果你想认真看这篇笔记，可以参考配套题单，这些题目在下文练习题中也会提到。

目录

  1. 什么是背包

  2. 01 背包

    1. 无优化

    2. 空间优化

    3. 构造 01 背包最优解

    4. 练习题

  3. 完全背包

    1. 定义

    2. 写法

    3. 练习题

  4. 恰好背包

    1. 思路

    2. 练习题

  5. 布尔及计数型背包

    1. 计数背包

    2. 布尔背包

    3. 练习题

  6. 尾声

什么是背包

背包属于动态规划（dp）的一种。

所以想学习背包，你要现对 dp 有基本的了解。

背包有很多种类，变形也很广泛，最基础的有：

  1. 01 背包

  2. 完全背包

  3. 多重背包

  4. 分组背包

  5. 计数背包

  6. 恰好背包

  7. 可行性背包（布尔背包）

  8. 混合背包

这些背包分别是用来干什么的呢？往下看。

这里先暂时只讲解几种背包的使用。

01 背包

01 背包（无优化）

最基础的 01 背包长这个样子：

  • 一个背包，容量为 \(m\)。
  • 有 \(n\) 个物品，每个物品有它的大小 \(w_i\) 与价值 \(p_i\)。
  • 求背包所能容纳的最大价值。

对于每个物品，有两种状态：选或不选，因此得名 01 背包。

最朴素的做法是 dfs() 枚举每样物品是否装进背包，时间复杂度 \(O(2^n)\)，太慢啦。

dfs() 的代码不给了，因为实现很简单因为重点是背包。

我们设 \(dp_{i, j}\) 表示：当背包容量为 \(j\) 时，使用前 \(i\) 个物品所能达到的最大价值。

状态转移方程可以根据一个物品选或不选来讨论。

如果不选，那么就是前 \((i-1)\) 个物品同样的容量，即： \(dp_{i-1, j}\)。

如果选，会复杂一些，请认真理解。

凑上第 \(i\) 个物品后容量为 \(j\)，说明前 \((i-1)\) 个物品对应的容量为 \((j - w_i)\)。

选这个物品是有价值加成的，所以还要加上 \(p_i\)。

选的推理会稍微复杂一些，但实际上，转移方程是很简单的：\(dp_{i-1, j - w_i} + p_i\)。

那么，最终的状态转移方程是选或不选的两种情况的较大值。

//下面这一行为状态转移方程。
dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + p[i]);

诶等等！别这么快就开始得瑟了。还有一个大坑点！

状态转移方程中有个 \(j - w_i\)，你有没有想过这个值变成负数会怎么办？

没错，会 \(\color{purple}{RE}\) 哦。所以在 for() 循环枚举 \(j\) 时，如果 \(j < w_i\)，那么 \(dp_{i, j}\) 就是 \(dp_{i-1, j}\)（也就是不选的结果）。

最终代码如下，时间复杂度 \(O(nm)\)。

#include <iostream>
#include <cstdio>
#define N 233
#define M 1005
using namespace std;
int w[N], p[N], dp[N][M];
int main()
{
	int m, n;
	scanf("%d%d", &m, &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &w[i], &p[i]);
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			if (j < w[i]) dp[i][j] = dp[i-1][j];
			else dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + p[i]);
		}
	printf("%d", dp[n][m]);
	return 0;
}

另外，可以用下面这组数据验证：

6 4
1 4
2 6
3 12
2 7

运行结果：

23

以下几个关于 01 背包的代码，验证数据都是这个。

01 背包（优化）

  1. 空间优化：

你会发现 dp 数组根本不需要开二维，用一维数组就够了。

因为每次 dp 数组都只需要使用前一层的内容更新，显然用滚动数组是个不错的选择。

不不不，你想多了，写滚动数组比二维数组还更容易呢！

代码如下：

#include <iostream>
#include <cstdio>
#define N 233
#define M 1005
using namespace std;
int w[N], p[N], dp[M];
int main()
{
	int m, n;
	scanf("%d%d", &m, &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &w[i], &p[i]);
	for (int i = 1; i <= n; i++)
		for (int j = m; j >= w[i]; j--)
			dp[j] = max(dp[j], dp[j - w[i]] + p[i]);
	printf("%d", dp[m]);
	return 0;
}

你会发现不需要判断 \(j - w_i < 0\) 的情况了，请仔细观察代码，找出原因。

构造 01 背包最优解

你可以运用本节的知识求出 01 背包使用了什么物品。

这一节是很多书本没有提到的，或许是因为很少题目考，但在实际生活中还是很有帮助的。

我们可以利用倒推的思想求出使用的物品。

注意！你必须使用第一种方法，因为只有第一种方法能存储不同状态的答案。

创建一个指针 \(k\) 表示：现在可以使用前 \(k\) 个物品。

由于我们是要倒推，\(k\) 应该先指向 \(n\)。

int k = n;  //创建指针。

如果选了 \(i\) 号物品，说明使用了 \(dp_{i-1, j - w_i} + p_i\)，为了好写，我们通常用 \(dp_{i, j} \ne dp_{i-1, j}\) 表示。

注：上面这个不等式的意思是：没有采用不选的结果。说明就是采用了选的结果。

代码还是很好打的，虽然会稍微长一些。

#include <iostream>
#include <cstdio>
#define N 233
#define M 1005
using namespace std;
int n, m, w[N], p[N], dp[N][M];
void backpack()  //把关键步骤写进函数里会更加美观。 
{
	for (int i = 1; i <= n; i++)
		for (int j = 1; j <= m; j++)
		{
			if (j < w[i]) dp[i][j] = dp[i-1][j];
			else dp[i][j] = max(dp[i-1][j], dp[i-1][j - w[i]] + p[i]);
		}	
}
int ans[N], cur;
void get_backpack()
{
	int k = m;
	for (int i = n; i >= 1; i--) //逆向枚举。
		if (dp[i][k] != dp[i-1][k])
			ans[++cur] = i, k -= w[i];
	printf("use:");
	for (int i = cur; i >= 1; i--) printf(" %d", ans[i]);
	printf(" to get the max price."); 
}
int main()
{
	scanf("%d%d", &m, &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &w[i], &p[i]);
	backpack();
	printf("max price = %d.\n", dp[n][m]);
	get_backpack();
	return 0;
}

测试数据同上，运行结果为：

max price = 23.
use: 1 3 4 to get the max price.

练习题

都是洛谷的题目。

必做题（难度都很低）：

  • P1048：01 背包模板题，一定先练习这一题。

  • P1060：01 背包变形题，但只需要对状态转移方程稍微改变。

  • P1734：先预处理，再执行 01 背包。这是很多题目使用的写法。

挑战题：

  • P1510：这题有两种写法，虽然都能通过，但不同的方向会直接影响到时间效率。

  • P1417：这题对于初学者来说是非常困难的。提示，需要结合排序，排序的 cmp 函数很有挑战。

下面介绍另一种背包。

完全背包

定义

  • 和 01 背包类似，不过每种物品有无限个。

  • 其他是一样的。

写法（直接是优化版）

我们直接对优化版的 01 背包进行更改。

不卖关子，更改方法很简单，第二层循环顺着来就好了。

正确性显然。

代码：

#include <iostream>
#include <cstdio>
#define N 233
#define M 1005
using namespace std;
int w[N], p[N], dp[M];
int main()
{
	int m, n;
	scanf("%d%d", &m, &n);
	for (int i = 1; i <= n; i++) scanf("%d%d", &w[i], &p[i]);
	for (int i = 1; i <= n; i++)
		for (int j = w[i]; j <= m; j++)  //只有这一行更改了。 
			dp[j] = max(dp[j], dp[j - w[i]] + p[i]);
	printf("%d", dp[m]);
	return 0;
}

测试数据与上文提到的相同，但输出应为：

24

所以，我们得到一个没用的关系式：

01 背包的结果 \(\le\) 完全背包的结果

练习题

必做题（简单题）：

  • P2722：完全背包模板题，一定要先打这一题。

  • P1679：学会预处理很重要，其他也是完全背包模板。

挑战题：

  • P2979：分类讨论，代码会稍长一些，相信自己一定能行！

恰好背包

思路

什么是恰好背包？老规矩，先看恰好背包的样子：

  • 物品的总价值需要恰好等于 \(n\)。

  • 01 背包与完全背包都适用。

  • 其他相同。

其实这个很简单，只需要在板子前加上：

memset(dp, -0x3f, sizeof(dp));
dp[0] = 0;

貌似很容易理解，请自行思考。

练习题

注意！这次的练习题都比较难。

  • UVA12563：别被难度欺骗，只不过算是半个板子，在最后输出的地方稍微更改罢了。

  • P2340：挺有挑战的哦，还需要使用滚动数组。

* 滚动数组大致写法：

//原先的
int dp[N][W];
dp[i][j] = max(dp[i-1][j], dp[i-1][j - s[i]] + f[i]);
//空间优化的
int dp[2][W];
dp[i%2][j] = max(dp[(i-1)%2][j], dp[(i-1)%2][j - s[i]] + f[i]);

布尔及计数型背包

计数背包

什么是计数背包呢？

顾名思义，是计算解法数量的。

大致长下面这个样子：

  • 给你 \(m\) 个数，每个数字有限或无限地使用。

  • 选取一些数，使这些数的和为 \(n\)。

  • 问有几种凑法（不考虑顺序）。

『有限』和『无限』表示了是使用 01 背包还是完全背包。

设 \(dp_i\) 表示得到 \(i\) 的方案数，则状态转移方程为：

\(dp_j = dp_j + dp_{j - a_i}\)

很容易理解，\((j - a_i)\) 的方案数，与再补一个 \(a_i\) 的方案数是有承接关系的。

对了，记得要初始化，例如本例中需要初始化 \(dp_0 = 1\)。

代码实际上也只是前面的模板稍作更改。

#include <iostream>
#include <cstdio>
using namespace std;
int a[2333], dp[2333];
int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i++) scanf("%d", &a[i]);
	dp[0] = 1;
	for (int i = 1; i <= m; i++)
		for (int j = a[i]; j <= n; j++) //例题是完全背包，如果是 01 背包逆序枚举即可。
			dp[j] += dp[j - a[i]];
	printf("%d", dp[n]);
	return 0;
}

接下来看布尔背包。

布尔背包

你首先会有疑问：

这是因为，两个背包比较相似。

长相也差不多：

  • 这次是求能否构造和为 \(n\) 的方案。

  • 其它都一样。

思路也可以延续计数背包，你还记得计数背包的状态转移方程吗？

dp[j] += dp[j - a[i]];

哈哈，布尔背包是差不多的：

dp[j] |= dp[j - a[i]];

这个 | 符号是『或符号』。它的运算规律如下：

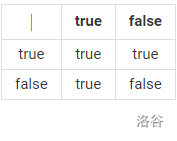
（前台表格炸了只能在后台截图）

观察上面的表，很容易发现，两边只要有一个是 true，返回的结果就是 true。

那么状态转移方程就很好理解了吧。

代码不是基本一样的吗。

#include <iostream>
#include <cstdio>
using namespace std;
int a[2333];
bool dp[2333];
int main()
{
	int n, m;
	scanf("%d%d", &n, &m);
	for (int i = 1; i <= m; i++) scanf("%d", &a[i]);
	dp[0] = true;
	for (int i = 1; i <= m; i++)
		for (int j = a[i]; j <= n; j++) 
			dp[j] |= dp[j - a[i]];
	printf("%d", dp[n]);
	return 0;
}

说了这么多，切几道题练习一下。

练习题

必做题（简单题）：

  • P2563：计数背包模板题，但是你要先学会质数筛。

  • P1049：半个布尔背包模板题。

  • P2347：自己判断这是什么类型的背包。

提升题（有点小难度）：

  • P1877：需要灵活运用布尔背包，把它扩充成二维背包会好做很多哦。

  • P1466：自己加油想一想，别忘记开 long long 哦。

挑战题：

  • P1504：读懂题，是成功的一半。

另注

不定时更新其他背包的写法。

如果有问题，请务必在评论区指出，避免误导后人。

不要脸地求大家点个赞吧！
首发：2022-04-19 22:26:23

posted @ 2022-08-25 00:32  liangbowen  阅读(22)  评论(1)  编辑  收藏  举报