[LeetCode题解]377. 组合总和 Ⅳ
前言
看完这篇题解,可以再看看这几个问题:
题目描述

题目:377. 组合总和 Ⅳ
解题思路
方法一:回溯 + 剪枝
采用前三题的思路:回溯 + 剪枝。
func combinationSum4(nums []int, target int) int {
if len(nums) == 0 {
return 0
}
sort.Ints(nums)
if target < nums[0] {
return 0
}
return backtrack(nums, target)
}
func backtrack(nums []int, target int) int {
if target == 0 {
return 1
}
res := 0
for i:=0;i<len(nums);i++ {
if target - nums[i] < 0 {
break
}
res += backtrack(nums, target-nums[i])
}
return res
}
结果超时QAQ。。。
方法二:回溯 + 剪枝 + 备忘录
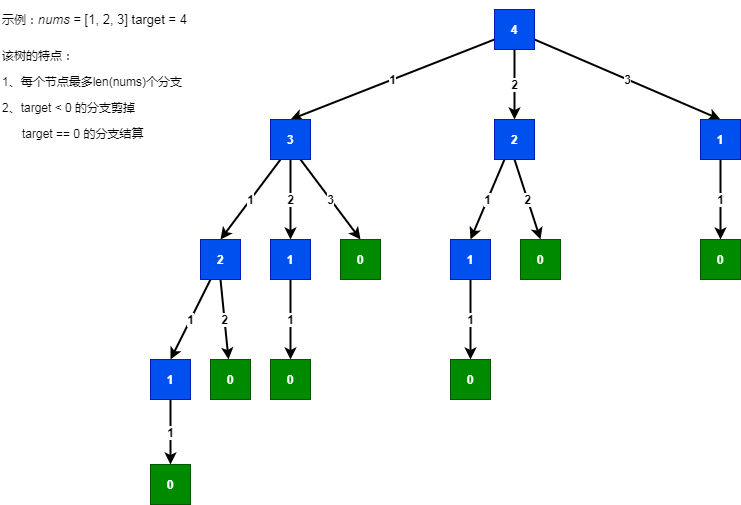
从方法一的代码生成的递归树可知,存在很多重复子问题。可以使用备忘录来降低时间复杂度。
var men []int
func combinationSum4(nums []int, target int) int {
if len(nums) == 0 {
return 0
}
men = make([]int, target+1)
sort.Ints(nums)
if target < nums[0] {
return 0
}
return backtrack(nums, target)
}
func backtrack(nums []int, target int) int {
if target == 0 {
return 1
}
if men[target] > 0{
return men[target]
}
res := 0
for i:=0;i<len(nums);i++ {
if target - nums[i] < 0 {
break
}
res += backtrack(nums, target-nums[i])
}
men[target] = res
return res
}
但是结果仍然超时QAQ。。。
方法三:DP
解决重复计算、重复子问题也可以使用 DP 来解决。
第一步:找重复性
通过递归树可知,存在重复计算了多次相同 target 的组合数。
第二步:定义状态
直接将问题转化为定义,dp[i] 表示 target=i 时的组合数。
第三步:找出 DP 方程
通过递归树得到 DP 方程如下:
dp[i] = sum(dp[i - num] for num in nums and if i >= num)
第四步:初始化状态
dp[0] = 1 表示对于给定数组的 target = 0 的结果有 1 个,即空集。
代码实现:
func combinationSum4(nums []int, target int) int {
dp := make([]int, target+1)
dp[0] = 1
for i:=1;i<=target;i++{
for _,num := range nums {
if i >= num {
dp[i] += dp[i-num]
}
}
}
return dp[target]
}
复杂度分析:
- 时间复杂度:\(O(n * target)\),其中
n是数组nums的长度。 - 空间复杂度:\(O(target)\)。使用
target + 1长度的数组空间。



