[LeetCode题解]40. 组合总和 II
前言
看完这篇题解,可以再看看这几个问题:
题目描述

题目:40. 组合总和 II
解题思路
本题与39. 组合总和类似,区别在于数据是否可以重复使用。
算法步骤:
- 排序。方便进行剪枝判断。
- 回溯。排列、组合类题目常用方法。
- 剪枝。提前去掉不符合的结果,降低时间复杂度。
- 去重。
如何去掉重复的集合(重点)
去重最简单的方法是使用哈希表,但是时间和空间复杂度会提高。
通过查看递归树(回溯本质是递归,会生成递归树)
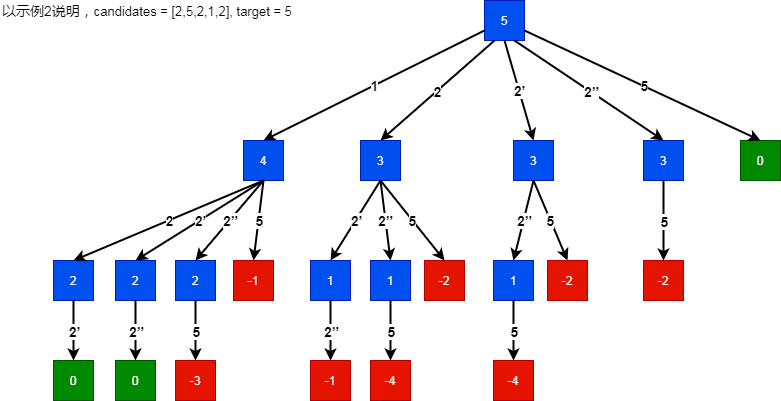
其中 [1,2,2'] 和 [1,2',2''] 是重复的。我们发现,出现重复的集合的原因是在同一层的出现相同的元素。
因此我们得到去重条件:相同元素只保留第一个,即去掉相同元素的非第一个元素。
if i > start && candidates[i] == candidates[i-1] {
continue
}
代码实现
var ans [][]int
var list []int
func combinationSum2(candidates []int, target int) [][]int {
// 1. 排序
// 2. 回溯 + 剪枝
ans = make([][]int, 0)
list = make([]int, 0)
if len(candidates) == 0 {
return ans
}
sort.Ints(candidates)
backtarck(candidates, 0, target)
return ans
}
func backtarck(candidates []int, start int, target int) {
// terminal
if target == 0 {
tmp := make([]int, len(list))
copy(tmp, list)
ans = append(ans, tmp)
return
}
// logical code
for i:=start;i<len(candidates);i++ {
if target - candidates[i] < 0 { // 剪枝:已排序的数组后面的数字差肯定都<0
break
}
if i > start && candidates[i] == candidates[i-1] { // 去重:去掉第一个
continue
}
list = append(list, candidates[i])
backtarck(candidates, i+1, target-candidates[i])
list = list[:len(list)-1]
}
}
复杂度分析:
- 时间复杂度:\(O(2^n * n)\),其中
n是数组candidates的长度。一般的递归树的时间复杂度是 \(O(2^n)\),遍历数组的时间复杂度是 \(O(n)\) ,最终时间复杂度为 \(O(2^n * n)\)。 - 空间复杂度:\(O(n)\)。除了保存结果的数组外,还需要一个数组保存回溯过程的中间结果。



