《数据结构与算法之美》22——递归树

前言

在排序那一节里，讲到排序时，利用递推公式推导时间复杂度来求解归并排序、快速排序的时间复杂度，但有些情况，例如快速排序的平均时间复杂度，利用递推公式，会涉及很复杂的数据推导。今天学习一种特殊的树来分析递归算法的时间复杂度，那就是递归树。

递归树与时间复杂度

递归算法的思路是把大问题分成小问题来解决，一层一层的分解，直到问题规模足够小，不需要再递归为止。

把这个一层一层的分解过程画成图，它其实是一颗树。给它起个名字叫递归树。下面是一棵斐波那契数列的递归树：

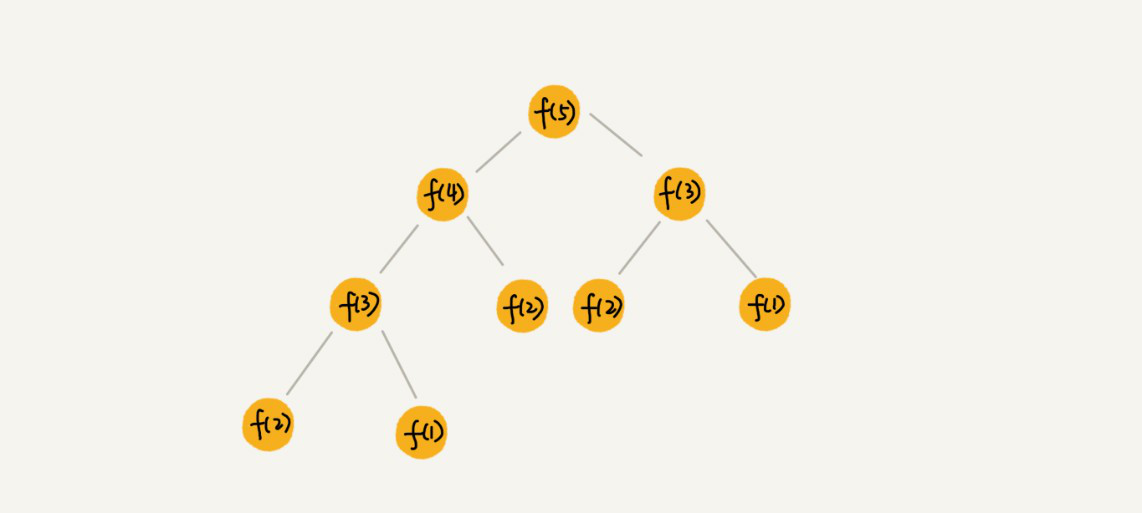
下面通过几个案例来介绍如何使用递归树来分析递归算法的时间复杂度。

实战案例

分析快速排序的时间复杂度

快速排序算法，通过选择一个数据作为pivot（分区点），将小于pivot的数据和大于pivot的数据进行交换，直到分区大小为1为止。

快速排序在最好的情况下，每次分区都能一分为二，这时候用递推公式T(n)=2T(n/2)+n，推导出时间复杂度是O(nlogn)。但是，并不可能每次分区都这么幸运，正好一分为二。

假设平均情况下，每次分区之后，两个分区的大小比例为1:k。当k=9时，用递推公式求解时间复杂度的话，递推公式就写成T(n)=T(f(n/10))+T(f(9n/10))，推导过程十分复杂。

用今天学习的递归树来分析，会简单不少，下面来看看分析过程。

把上面例子的递归分解的过程画成递归树，如下：

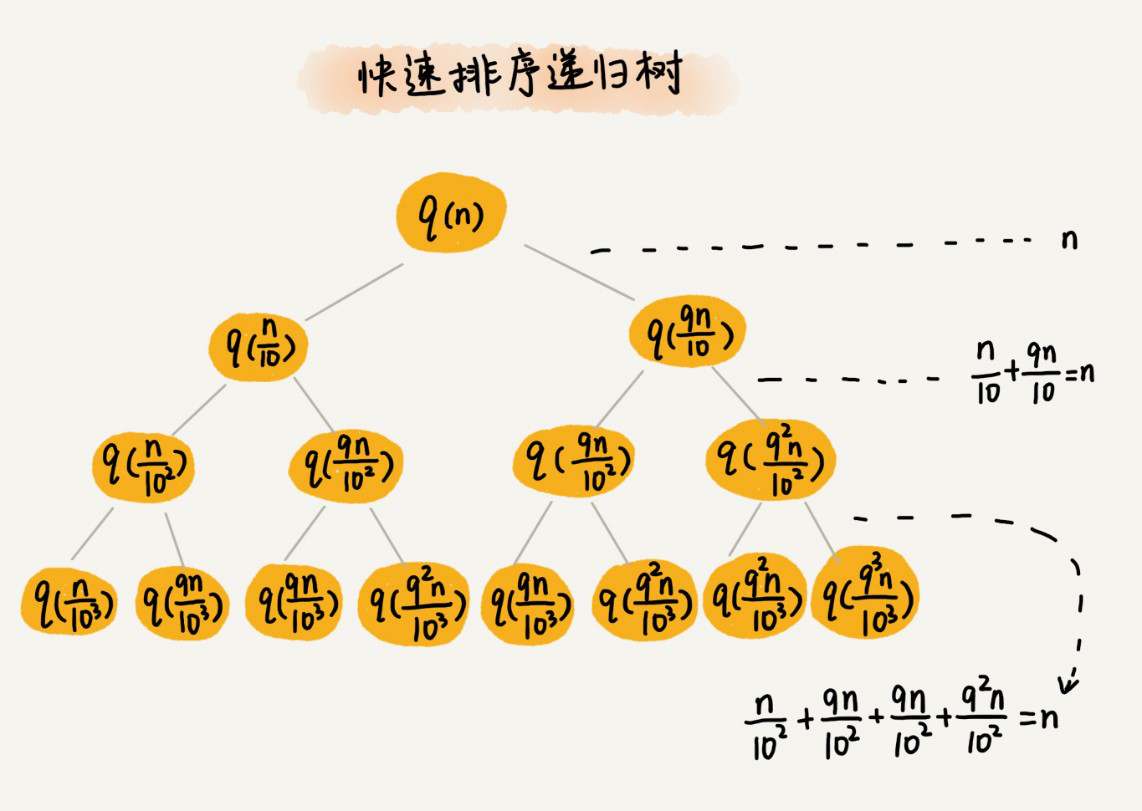
通过计算，可以得到，从根节点到叶子节点的最短路径是log₁₀n，最长路径是log_10/9n。

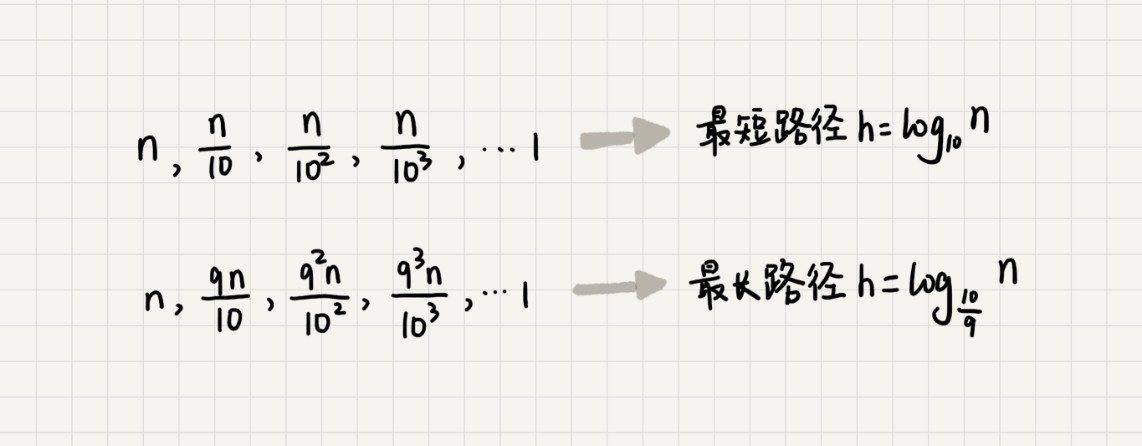
所以，遍历数据的个数总和就介于nlog₁₀n和nlog_10/9n之间。根据复杂度的大O表示法，统一写成O(nlogn)。

刚刚假设k=9，实际上不管k是多少，都是一个确定的常量，那时间复杂度还是O(nlogn)。

分析斐波那契数列的时间复杂度

下面介绍的例子是斐波那契数列，代码如下：

int f(int n) {
 if (n == 1) return 1;
 if (n == 2) return 2;
 return f(n-1) + f(n-2);
}

把上面的递归代码画成递归树，如下：

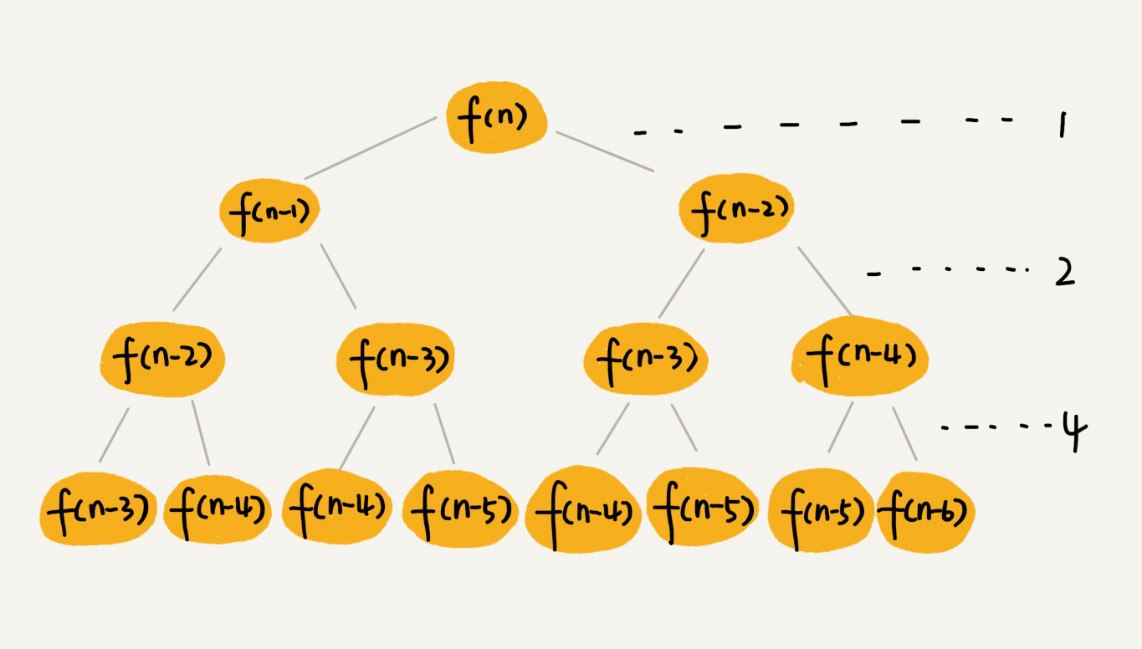
f(n)分解为f(n-1)+f(n-2)，每次数据规模都是1或者2，叶子节点的数据规模是1或者2。所以从根节点走到叶子节点，每条路径是长短不一的。如果每次都是1，那最长路径是n，如果每次都是2，那最短路径是n/2。

每次分解之后的合并操作只需要一次加法运算，把这次加法运算的时间消耗记作1。从上往下，第一层是1，第二层是2，第三层是2²。以此类推，第k层的时间消耗是2^k-1。

如果路径长度是n，那这个总和就是2ⁿ-1。

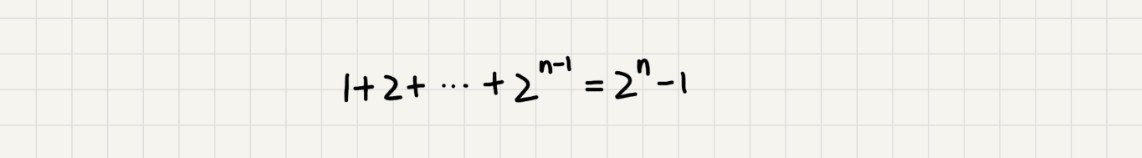
如果路径长度是n/2，那总的时间消夏就是2^n/2-1。

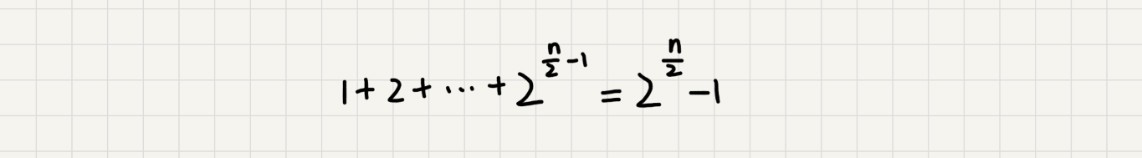
所以，这个算法的时间复杂度就介于O(2ⁿ)和O(2^n/2)之间，是指数级的。

分析全排列的时间复杂度

前两个比较简单，来看一个稍微复杂的。

高中时都学过排列组合。“如何把n个数据的所有排列都找出来”，这就是全排列的问题。

举个例子，比如，1，2，3这个集合，有下面的几种不同的排列：

1, 2, 3
1, 3, 2
2, 1, 3
2, 3, 1
3, 1, 2
3, 2, 1

如何编程打印一组数据的所有排列呢，这里可以用递归来实现。

如果确定了最后一位数据，那就变成了求解剩下n-1个数据的排列问题。而最后一位数据就是n个数据中的任意一个，因此它的取值有n种情况。所以，“n个数据的排列”问题，就分解成n个“n-1个数据的排列”的子问题。

写成递推公式，如下：

假设数组中存储的是1，2， 3...n。

f(1,2,...n) = {最后一位是1, f(n-1)} + {最后一位是2, f(n-1)} +...+{最后一位是n, f(n-1)}。

把递推公式写成代码，如下：

// 调用方式：
// int[]a = a={1, 2, 3, 4}; printPermutations(a, 4, 4);
// k表示要处理的子数组的数据个数
public void printPermutations(int[] data, int n, int k) {
    if (k == 1) {
        for (int i = 0; i < n; ++i) {
            System.out.print(data[i] + " ");
        }
        System.out.println();
    }
    for (int i = 0; i < k; ++i) {
        int tmp = data[i];
        data[i] = data[k-1];
        data[k-1] = tmp;
        printPermutations(data, n, k - 1);
        tmp = data[i];
        data[i] = data[k-1];
        data[k-1] = tmp;
    }
}

下面来看一下如何借助递归树来分析时间复杂度。

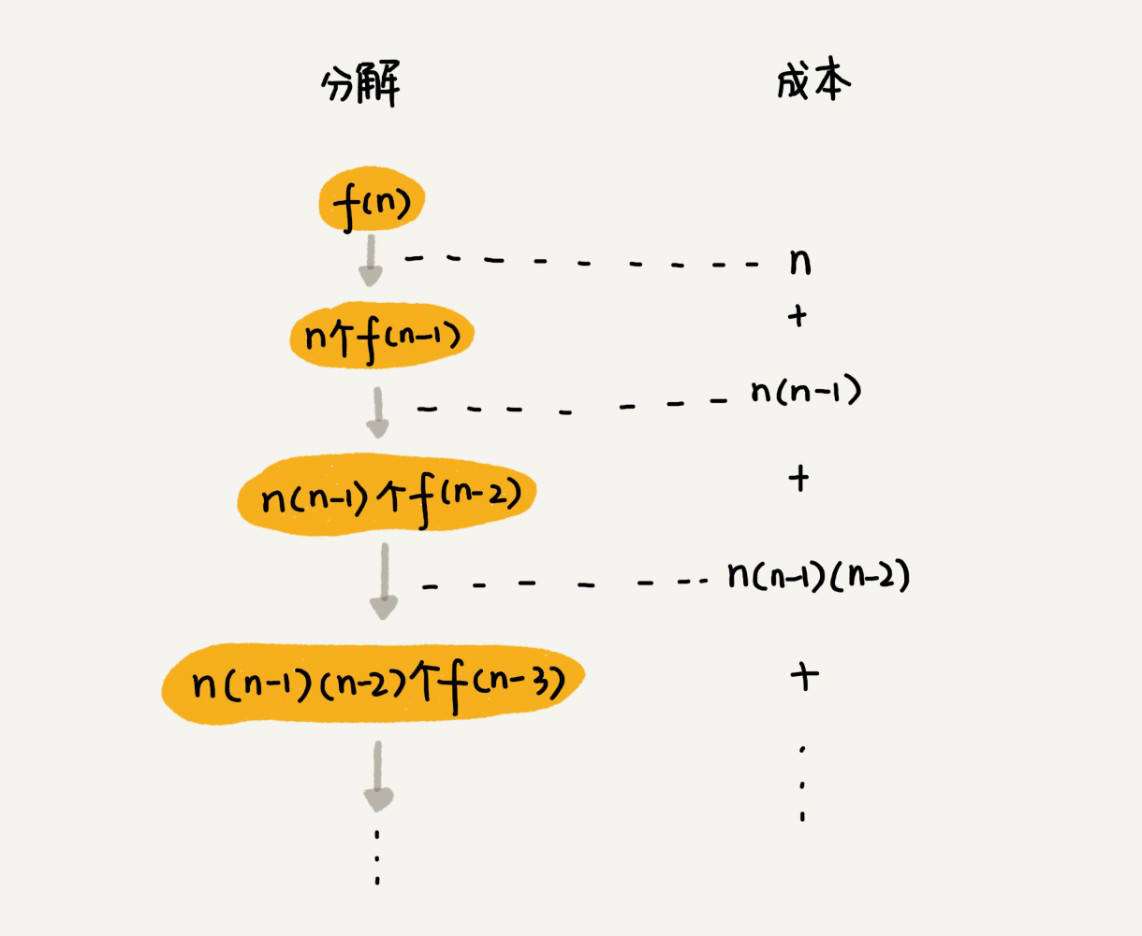
第一层分解有n次交换操作，第二层有n*(n-1)，第三层n*(n-1)*(n-2)。

以此类推，第k层就是n*(n-1)*(n-2)....*(n-k+1)，最后一层就是n*(n-1)*(n-2)....*2*1。

每一层的总和是：

\(n + n*(n-1) + n*(n-1)*(n-2) +... + n*(n-1)*(n-2)*...*2*1\)

这个公式的求和比较复杂，我们看最后一个数，n*(n-1)*(n-2)....*2*1等于n!，前面的n-1个数都小于最后一个数，所以，总和肯定小于n*n!，也就是说，全排列的递归算法的时间复杂度大于O(n!)，小于O(n*n!)。

分析细胞分解的时间复杂度

1个细胞的生命周期是3小时，1小时分裂一次。求n小时后，容器内有多少细胞？

第0小时，存活1个细胞；第1小时，存活2个细胞；第2小时，存活4个细胞；第3小时，存活8（前第3小时的细胞数）个细胞；第4小时，存活16-1（前第3小时的细胞数）个细胞；以此类推，第k小时，存活2^k-2^k-3。

递推公式如下：

\(f(0)=1\)
\(f(1)=2\)
\(f(2)=4\)
\(f(n)=2f(n-1)-f(n-4)\)

将递推公式画成递归树：

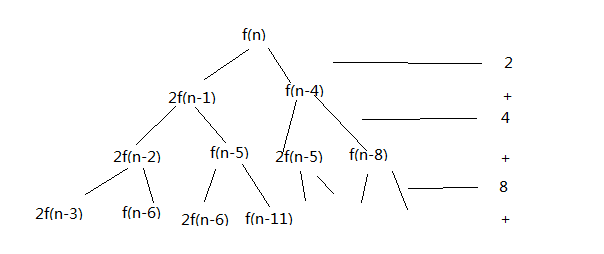
与分析斐波那契数列的时间复杂度类似的计算方式，最长路径n+1，最短路径n-3；

假设乘法和减法的消耗是1，最长路径的消耗是

\(1+2+2^2+2^3+2^4+....+2^{n-1}=2^n-1\)

最短路径的消耗是

\(1+2+2^2+2^3+2^4+....+2^{n-4}=2^{n-3}-1\)

因此时间复杂度在O(2^n-1)到O(2^n-3)之间，是指数级的。

总结

今天讲了如何用递归树来分析递归算法，再加上前面学习排序时介绍的递推公式，就有两种分析递归算法的时间复杂度的方法了。

在分析时间复杂度时，要根据情况，灵活使用。有些代码适合使用递推公式，比如归并排序的时间复杂度；有些代码适合递归树，比如快速排序的平时时间复杂度；有些代码两种方法都不适合。比如二叉树的递归前中后序遍历的时间复杂度。

总之，平时要多练，多分析。