Day 40

第130题：

给定一个二维的矩阵，包含 'X' 和 'O'（字母 O）。

找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。(来自LeetCode)

 

1、分析二维矩阵内的哪一部分 O 是被包围的呢；

　　其实二维矩阵内有三种类型的字符：第一种是 X ，第二种是被包围的 O ，第三种是没有被包围的 O；

　　如果我们需要把被包围的 O 变成 X ，可以转换思路，寻找没有被包围的 O ，然后对这些 O 做上标记；

　　再遍历二维矩阵，将矩阵内没有标记的 O 变为 X。

　　其中没有被包围的 O 一定存在矩阵的边缘或者和矩阵边缘的 O 相邻，我们只需要遍历矩阵的上下左右四边的位置；

　　如果是 O ,将这个 O 变成 A (相当于做标记)，再遍历这个位置上下左右是否存在 O ；

　　只要有，那它肯定不是被包围的 O ，也变成 A ，这样就可以找出所有的不被包围的 O ；

　　最后遍历矩阵，将 A 变回 O ，把 O 变成 X 即可。

　　

第122题：

给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你可以尽可能地完成更多的交易（多次买卖一支股票）。

注意：你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。来源：力扣（LeetCode）

 

1、为求最大收益，就是把每一次可以得到的收益都累计起来；

　　那么当我们买入一只A，遍历下一个B，涨了，卖出，得到收益profit1；

　　然后可以看作把卖出的又买回来B，再遍历下一个C，如果没有涨，我们就将手中B的卖出，买下一个C；

　　那么这样就相当于把内部的所有利润都累计起来，得出最大利润profit。

　　

 

 2、也可以利用dp[x][y]数组判断此时的持有物(股票或者现金)和此时手中的收益；

　　x表示此时手中的收益(可为负数)，y表示持有现金或者股票(0：现金，1：股票)；

　　一开始dp[0][0]表示还没有开始交易，且持有现金；

　　当买入第一支股票（价值1）后，就改为dp[-1][1]；

　　然后遍历整个数组，得出每个位置买入或者卖出后的转台存入dp数组；

　　最终得出最大值。

　　

第136题：

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗。来源：力扣（LeetCode）

 

 

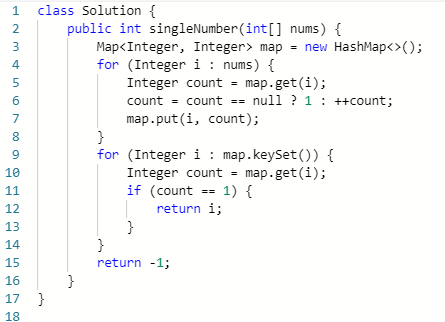
 1、遍历数组，将元素和元素的个数存入hash表，然后遍历hash表，得出个数为1的元素。

　　

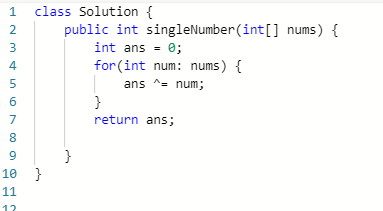
2、利用亦或性质，数组中的全部元素的异或运算结果即为数组中只出现一次的数字。

　　

 

class Solution {    public int singleNumber(int[] nums) {        Map<Integer, Integer> map = new HashMap<>();        for (Integer i : nums) {            Integer count = map.get(i);            count = count == null ? 1 : ++count;            map.put(i, count);        }        for (Integer i : map.keySet()) {            Integer count = map.get(i);            if (count == 1) {                return i;            }        }        return -1; // can't find it.    }}
作者：yinyinnie链接：https://leetcode-cn.com/problems/single-number/solution/xue-suan-fa-jie-guo-xiang-dui-yu-guo-cheng-bu-na-y/来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。