数据结构--循环队列
一.顺序队列的改进
队列元素的出列是在队头,即下标为0的位置,那也就意味着,队列中的所有元素都得向前移动,以保证队列的队头(也就是下标为0的位置)不为空,此时的时间复杂度为0(n)。
可有时想想,为什么出队列时一定要全部移动呢,如果不去限制队列的元素必须存储在数组的前n个单元这一条件,出队的性能就会大大增加。也就是说,队头不需要一定在下标为0的位置,比如也可以是a[1]等。
而为了避免当只有一个元素时,队头和队尾重合使处理变得麻烦,引入两个指针,front指针指向队头元素,rear指针指向队尾元素的下一个位置,这样当front等于rear时,此队列不是还剩一个元素,而是空队列。
对于队列最好的方法是使用链表实现,因为对于数组来说,队列可能会出现下面这种情况:
假设是长度为5的数组,初始状态,空队列如所示,front与 rear指针均指向下标为0的位置。然后入队a1、a2、a3、a4, front指针依然指向下标为0位置,而rear指针指向下标为4的位置。

出队a1、a2,则front指针指向下标为2的位置,rear不变,如下图所示,再入队a5,此时front指针不变,rear指针移动到数组之外。嗯?数组之外,那将是哪里?

问题还不止于此。假设这个队列的总个数不超过5个,但目前如果接着入队的话,因数组末尾元素已经占用,再向后加,就会产生数组越界的错误,可实际上,我们的队列在下标为0和1的地方还是空闲的。我们把这种现象叫做“假溢出”。
不可以继续添加元素,否则会造成数组越界而遭致程序出错。然而此时又不应该扩充数组,因为还有大量实际空间未被占用。
此时我们应该如何解决这个问题呢?我们将其实现为循环队列。
解决假溢出的办法就是后面满了,就再从头开始,也就是头尾相接的循环。我们把队列的这种头尾相接的顺序存储结构称为循环队列。
也就是利用循环来解决空间浪费问题。
二.循环队列的引入
2.1总结来说,什么是循环队列?
由于在用数组实现队列的时候,队列有元素出列,front就向后移动,所以队列前面的空间就空了出来。当rear移动到LENGTH时,再入队会发生假溢出,也就是说实际上我们开辟的数组还有剩余空间,却因为rear越界表现为溢出,
为了更合理的利用空间,人们想了一个办法:将队列的首尾相连接。这样当rear移动到LENGTH时,会再从0开始循环。
那当什么时候队列满呢?当rear等于front的时候。可是队列为空的时候也是同样的条件,那不就没法判断了吗?
办法一是设置一个标志变量flag,当front == rear,且flag = 0时为队列空,当front == rear,且flag= 1时为队列满
办法二牺牲一个存储空间,front前面不存数据,当rear在front前面的时候就是满了(尾在头前就是满了)
我们主要讨论第二种方法=
2.2理解循环队列
当队列空时,条件就是from = rear,当队列满时,我们修改其条件,保留一个元素空间。也就是说,队列满时,数组中还有一个空闲单元。 如下图所示,我们就认为此队列已经满了,
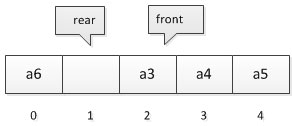
由于rear可能比front大,也可能比front小,所以尽管它们只相差一个位置时就是满的情况,但也可能是相差整整一圈。所以若队列的最大尺寸为QueueSize,那么队列满的条件是(rear+1) %QueueSize == front (取模“%的目的就是为了整合rear与front大小为一个问题)。
比如上面这个例子, QueueSize = 5,当 front=0,而 rear=4, (4+1) %5 = 0,所以此时队列满。再比如,front = 2而rear =1。(1 + 1) %5 = 2,所以此时 队列也是满的。而对于下图, front = 2而rear= 0, (0+1) %5 = 1,1!=2,所以此时队列并没有满。

另外,当rear > front时,此时队列的长度为rear—front。但当rear < front时,队列长度分为两段,一段是QueueSize-front,另一段是0 + rear,加在一起,队列长度为rear-front + QueueSize,
因此通用的计算队列长度公式为:
(rear—front + QueueSize) % QueueSize
总结
队空条件:front == rear
队满条件:(rear+1) %QueueSize == front
队列长度:(rear—front + QueueSize) % QueueSize
三.循环队列的代码
3.1.循环队列各个参数的含义
(1)队列初始化时,front和rear值都为零;
(2)当队列不为空时,front指向队列的第一个元素,rear指向队列最后一个元素的下一个位置;
(3)当队列为空时,front与rear的值相等,但不一定为零;
3.2循环队列入队的伪算法
(1)把值存在rear所在的位置;
(2)rear=(rear+1)%maxsize ,其中maxsize代表数组的长度;
bool Enqueue(PQUEUE Q, int val)
{
if(FullQueue(Q))
return false;
else
{
Q->pBase[Q->rear]=val;
Q->rear=(Q->rear+1)%Q->maxsize;
return true;
}
}
3.3.循环队列出队的伪算法
(1)先保存出队的值;
(2)front=(front+1)%maxsize ,其中maxsize代表数组的长度;
bool Dequeue(PQUEUE Q, int *val)
{
if(EmptyQueue(Q))
{
return false;
}
else
{
*val=Q->pBase[Q->front];
Q->front=(Q->front+1)%Q->maxsize;
return true;
}
}
3.4.如何判断循环队列是否为空
if(front==rear)
队列空;
else
队列不空;
bool EmptyQueue(PQUEUE Q)
{
if(Q->front==Q->rear) //判断是否为空
return true;
else
return false;
}
3.5.如何判断循环队列是否为满
解决这个问题有两个办法:一是增加一个参数,用来记录数组中当前元素的个数;第二个办法是,少用一个存储空间,也就是数组的最后一个存数空间不用,当(rear+1)%maxsiz=front时,队列满;
bool FullQueue(PQUEUE Q)
{
if(Q->front==(Q->rear+1)%Q->maxsize) //判断循环链表是否满,留一个预留空间不用
return true;
else
return false;
}
完整代码
queue.h文件代码:
#ifndef __QUEUE_H_
#define __QUEUE_H_
typedef struct queue
{
int *pBase;
int front; //指向队列第一个元素
int rear; //指向队列最后一个元素的下一个元素
int maxsize; //循环队列的最大存储空间
}QUEUE,*PQUEUE;
void CreateQueue(PQUEUE Q,int maxsize);
void TraverseQueue(PQUEUE Q);
bool FullQueue(PQUEUE Q);
bool EmptyQueue(PQUEUE Q);
bool Enqueue(PQUEUE Q, int val);
bool Dequeue(PQUEUE Q, int *val);
#endif
queue.c文件代码:
#include<stdio.h>
#include<stdlib.h>
#include"malloc.h"
#include"queue.h"
/***********************************************
Function: Create a empty stack;
************************************************/
void CreateQueue(PQUEUE Q,int maxsize)
{
Q->pBase=(int *)malloc(sizeof(int)*maxsize);
if(NULL==Q->pBase)
{
printf("Memory allocation failure");
exit(-1); //退出程序
}
Q->front=0; //初始化参数
Q->rear=0;
Q->maxsize=maxsize;
}
/***********************************************
Function: Print the stack element;
************************************************/
void TraverseQueue(PQUEUE Q)
{
int i=Q->front;
printf("队中的元素是:\n");
while(i%Q->maxsize!=Q->rear)
{
printf("%d ",Q->pBase[i]);
i++;
}
printf("\n");
}
bool FullQueue(PQUEUE Q)
{
if(Q->front==(Q->rear+1)%Q->maxsize) //判断循环链表是否满,留一个预留空间不用
return true;
else
return false;
}
bool EmptyQueue(PQUEUE Q)
{
if(Q->front==Q->rear) //判断是否为空
return true;
else
return false;
}
bool Enqueue(PQUEUE Q, int val)
{
if(FullQueue(Q))
return false;
else
{
Q->pBase[Q->rear]=val;
Q->rear=(Q->rear+1)%Q->maxsize;
return true;
}
}
bool Dequeue(PQUEUE Q, int *val)
{
if(EmptyQueue(Q))
{
return false;
}
else
{
*val=Q->pBase[Q->front];
Q->front=(Q->front+1)%Q->maxsize;
return true;
}
}
参考资料:
http://blog.csdn.net/lpp0900320123/article/details/20694409





