各种排序算法的python实现
各种排序算法的python实现
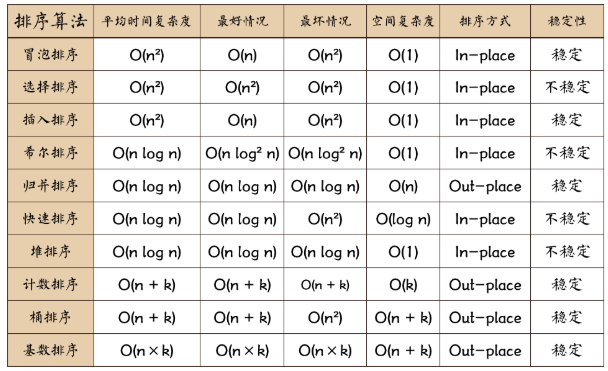
- 稳定:如果a原本在b前面,而a=b,排序之后a仍然在b的前面;
- 不稳定:如果a原本在b的前面,而a=b,排序之后a可能会出现在b的后面;
- 内排序:所有排序操作都在内存中完成;
- 外排序:由于数据太大,因此把数据放在磁盘中,而排序通过磁盘和内存的数据传输才能进行;
- 时间复杂度: 一个算法执行所耗费的时间。
- 空间复杂度:运行完一个程序所需内存的大小。
算法总结
一、冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
def BubbleSort(self,array):
if array==None or len(array)==0:
return
n = len(array)
# 设置一个标记,检测是否在每轮循环中发生了交换
flag = True
while n>=1 and flag:
flag = Flase
for i in range(n):
if array[i] > array[i+1]:
array[i],array[i+1] = array[i+1], array[i]
flag=True
n -= 1
return array二、插入排序
插入排序(Insertion-Sort)的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。插入排序在实现上,通常采用in-place排序(即只需用到O(1)的额外空间的排序),因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
def insertionSort(arr):
if arr==None or len(arr)==0:
return
for i in range(1, len(arr)):
key = arr[i]
j = i-1
while j >=0 and key < arr[j]:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = key
return arr三、选择排序
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
def selectSort(arr):
if arr==None or len(arr)==0:
return
for i in range(len(arr)):
min = i
# 不断找出未排序数组中最小的数
for j in range(1,len(arr)):
if arr[j]<arr[min]:
min = j
arr[i],arr[min] = arr[min],arr[i]
return arr四、希尔排序
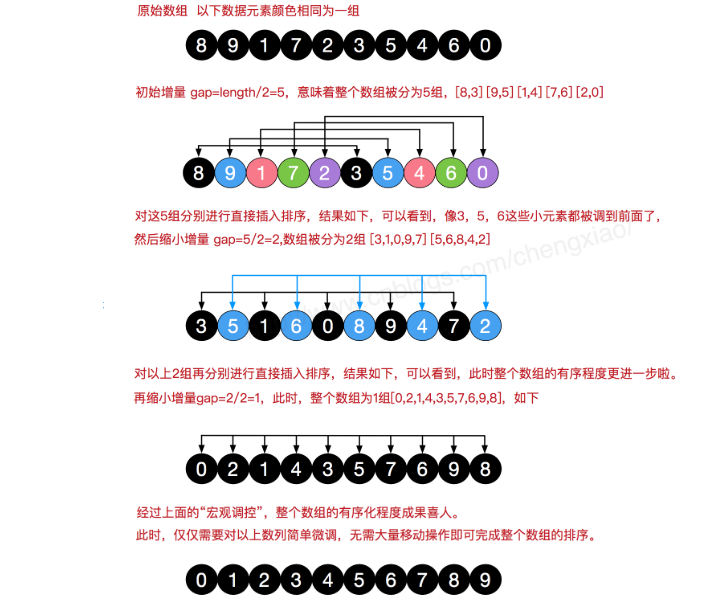
希尔排序是希尔(Donald Shell)于1959年提出的一种排序算法。希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
希尔排序是把记录按下表的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
图片演示:
def shellSort(nums):
n = len(nums)
gap = int(n/2)
while gap > 0:
for i in range(gap,n):
temp = nums[i]
j = i
while j >= gap and nums[j-gap] >temp:
arr[j] = nums[j-gap]
j -= gap
nums[j] = temp
gap = int(gap/2)
return nums五、归并排序
和选择排序一样,归并排序的性能不受输入数据的影响,但表现比选择排序好的多,因为始终都是O(n log n)的时间复杂度。代价是需要额外的内存空间。
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。归并排序是一种稳定的排序方法。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并
def mergeSort(arr):
if arr==None or len(arr)==0:
return
mid = len(arr) // 2
left = self.mergeSort(arr[:mid])
right = self.mergeSort(arr[mid:])
return self.merge(left,right)
def merge(self,left,right):
sortedArr = []
l = 0
r = 0
while l< len(left) and r<len(right):
if left[l] < right[r]:
sortedArr.append(left[l])
l += 1
else:
sortedArr.append(right[r])
r += 1
sortedArr += left[l:]
sortedArr += right[r:]
return sortedArr六、快速排序
快速排序的基本思想:通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
def Partition(L, left, right):
pivotkey = L[left]
while left < right:
while left < right and L[right] >= pivotkey:
right -= 1
L[left] = L[right]
while left < right and L[left] <= pivotkey:
left += 1
L[right] = L[left]
L[left] = pivotkey
return left
def q_sort(L, left, right):
if left < right:
pivot = Partition(L, left, right)
q_sort(L, left, pivot - 1)
q_sort(L, pivot + 1, right)
return L七、堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
def heap(arr,n,i):
largest = i
l = 2*i + 1
r = 2*i + 2
# 判断每个节点的左节点是否比该节点大
if l<n and arr[i]<arr[l]:
largest = l
# 判断右节点是否大于当前最大节点
if r<n and arr[largest]<arr[r]:
largest = r
# 如果堆顶元素发生变化
if largest!=i:
arr[i],arr[largest] = arr[largest],arr[i]
heap(arr,n,largest)
def heap_sort(arr):
n = len(arr)
# 建立最大堆,由下往上构建
for i in range(n,-1,-1):
heap(arr,n,i)
# 一次使用最后面的元素与堆顶元素进行交换
for j in range(n-1,0,-1):
arr[j],arr[0] = arr[0],arr[j]
head(arr,j,0)
return arr八、计数排序
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
计数排序(Counting sort)是一种稳定的排序算法。计数排序使用一个额外的数组C,其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。它只能对整数进行排序。
def count_sort(nums):
res = []
# 假设nums包括0这个数,建立一个全为零的数组
count = [0]*(len(nums))
# 统计每个位置上每个数出现的次数
for i in range(len(nums)):
count[nums[i]] += 1
# 如果每个位置上的数不为零,则一次打印直到打印完每个位置上的数
for i in range(len(nums)):
while count[i]:
res.append(i)
count[i] -= 1
return res九、桶排序
桶排序是将待排序集合中处于同一个值域的元素存入同一个桶中,也就是根据元素值特性将集合拆分为多个区域,则拆分后形成的多个桶,从值域上看是处于有序状态的。对每个桶中元素进行排序,则所有桶中元素构成的集合是已排序的。
def bucket_Sort(nums):
maxnum,minnum = max(nums),min(nums)
bucketArr = [[] for i in range(maxnum//10 - minnum//10 + 1)]
for i in nums:
index = i//10 - minnum//10
bucketArr[index].append(i)
# 清空原数组并把每个桶中的数排序后加入该数组中
nums.clear()
for i in bucketArr:
i.sort()
nums.extend(i)十、基数排序
基数排序也是非比较的排序算法,对每一位进行排序,从最低位开始排序,复杂度为O(kn),为数组长度,k为数组中的数的最大的位数;
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以是稳定的。
der radix_sort(nums):
i = 0
# 找出最大值
maxnum = max(nums)
# 得到最大值的长度
len = len(str(maxnum))
while i<len:
# 生成0-9共10个块来存储数字
bucket_list = [[] for _ in range(10)]
for num in nums:
# 将每个数字存储相应的块中,先按个位数,再按十位数。。。
bucket_list[(num/(100*i))%10].append(num)
nums.clear()
# 将每个块中的数再存入清空后的原数组
for x in bucker_list:
for item in x:
nums.append(item)
i += 1
return nums


 浙公网安备 33010602011771号
浙公网安备 33010602011771号