R语言：规划求解优化ROI

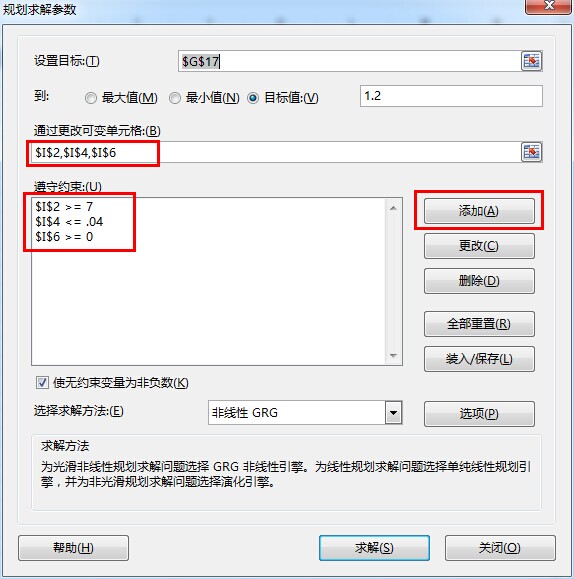
今天看到一篇文章介绍如何用excel建模对ROI 进行规划求解。
蓝鲸的网站分析笔记

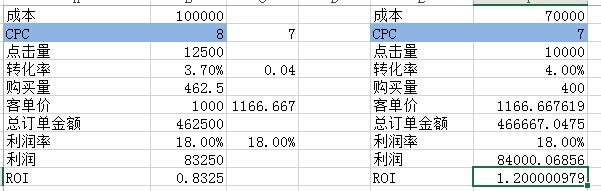
• 成本 Cost
• 每次点击费用 CPC
• 点击量 $$clickRate = \frac{cost}{CPC}$$
• 转化率 conversionRatio
• 购买量 $$Purchaseamount = \frac{Cost*conversionRatio}{CPC}$$
• 客单价 perCustomerTransaction
• 利润率 rateofProfit
• 利润 $$profit = Purchaseamount * perCustomerTransaction * rateofProfit$$
• 投资回报率 $$ ROI = \frac{profit}{Cost}$$

涉及 多元非线性规划分析求解 ,R 中提供了Rdonlp2()包。

library(Rdonlp2)
p<-c(7,0.01,1000)      # 迭代初始值
par.l=c(7,0,0);par.u=c(Inf,0.04,Inf) #自变量定义域约束
fn=function(x){
  0.18*x[2]*x[3]/x[1]
}  #目标函数

nlcon=function(x){
  0.18*x[2]*x[3]/x[1]
}
nlin.l=1.2;nlin.u=1.2 #构成非线性约束
ret<-donlp2(p,fn,par.u=par.u, par.l=par.l,
            nlin=list(nlcon), nlin.u=nlin.u, nlin.l=nlin.l)
ret

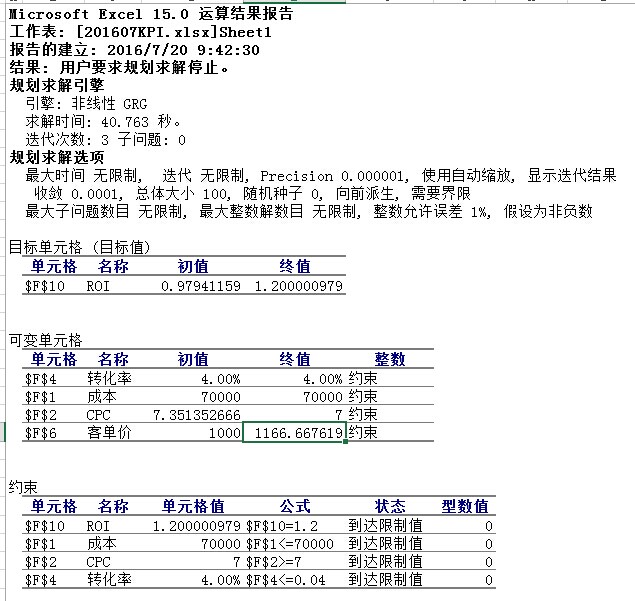
运行后的结果如下

 ret
$par   #DONLP2 的返回值 和Excel求解值相同
[1]    7.000    0.040 1166.667

$gradf  #梯度
[1] -0.171428571 30.000000000  0.001028571

$u   # vector of lagrange multipliers for constraints  约束拉格朗日乘子的矢量
[1] 5.551115e-17 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
[7] 1.000000e+00 0.000000e+00

$w   #vector of penalty term 惩罚因子向量
[1] 1.0 1.0 1.0 1.0 1.0 1.0 2.2 1.0

$step.nr  # total number of iterations 迭代次数
[1] 2

$fx  # the value of objective function fn  目标函数fn的结果
[1] 1.2

$scf  # scaling of fn 尺度
[1] 1

$psi # psi the weighted penalty term
[1] 0.3771429

$upsi # 
[1] 0.1714286

$del.k.1
[1] 0.001

$b2n0
[1] 0

$b2n
[1] 1.509644e-14

$nr
[1] 3

$sing
[1] -1

$umin
[1] 0

$not.used
[1] 0

$cond.r
[1] 17672.02

$cond.h
[1] 2.001279

$scf0
[1] 1

$xnorm
[1] 1000.025

$dnorm
[1] 166.6667

$phase
[1] 0

$c.k
[1] 1

$wmax
[1] 2.2

$sig.k
[1] 1

$cfincr
[1] 2

$dirder
[1] -0.2057143

$dscal
[1] 1

$cosphi
[1] 1e-05

$violis
[1] 0

$hesstype
[1] 0

$modbfgs
[1] 0

$modnr
[1] 0

$qpterm
[1] 0

$tauqp
[1] 0

$infeas
[1] 0

$nr.update
         [,1]         [,2]          [,3]
[1,] 1.000008 -0.005714053 -1.142493e-07
[2,] 0.000000  1.414665735  1.964581e-05
[3,] 0.000000  0.000000000  1.000000e+00

$message
[1] "KT-conditions satisfied, no further correction computed"

$runtime
[1] 0.002