精典算法之详解 河内之塔
河内之塔(Towers of Hanoi)是法国人M.Claus(Lucas)于1883年从泰国带至法国的,河内为越战时北越的首都,即现在的胡志明市;1883年法国数学家Edouard Lucas曾提及这个故事,据说创世
纪时Benares有一座波罗教塔,是由三支钻石棒(Pag)所支撑,开始时神在第一根棒上放置64个由上至下依由小至大排列的金盘(Disc),并命令僧侣将所有的金盘从第一根石棒移至第三根
石棒,且搬运过程中遵守大盘子在小盘子之下的原则,若每日仅搬一个盘子,则当盘子全数搬运完毕之时,此塔将毁损,而也就是世界末日来临之时。
我们来把这个故事变成一个算法:
把三个柱子标为ABC 如果只有一个盘子时,将它直接搬到c,当有两个盘子,就将B做为辅助。如果盘数超过2个,将第三个以下的盘子遮起来,就很简单了,每次处理两个盘子,也就是
A->B A->C B->C这三个步骤,而被遮住的部分是一个递归处理。如果有n个盘子,则移动完毕所需的次数为2^n-1。
看一下图,代码我会用c#和c++两种语言给出算法,然后我会把算法详细分解给大家
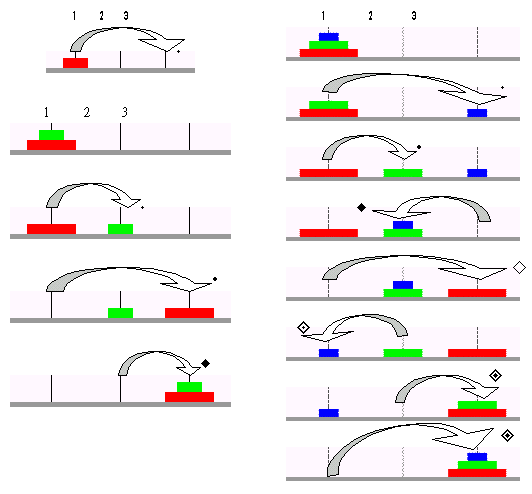
c++代码
void hanoi(int n,char A,char B,char C)
{
if(n==1)
{
cout<<"Move "<<n<<" from "<<A<<" to "<< C <<endl;
}
else
{
hanoi(n-1,A,C,B); //把A柱子上第N-1个盘子通过C放到B柱子上
cout<<"Move "<< n<<" from "<< A <<" to "<< C <<endl;
hanoi(n-1,B,A,C); //把B上所有盘子通过A放到C上
}
}
int main()
{
cout<<"请输入盘子数量"<<endl;
int n;
cin>>n;
hanoi(n,'A','B','C');
return 0;
}
c#代码
static void Main(string[] args)
{
Console.WriteLine("输入盘子数量");
int _n = Convert.ToInt32(Console.ReadLine());
Hanoi(_n, 'A', 'B', 'C');
Console.ReadLine();
}
static void Hanoi(int n, char A, char B, char C)
{
if (n == 1)
{
Console.WriteLine("Move {0} From {1} to {2}", n, A, C);
}
else
{
Hanoi(n - 1, A, C, B);
Console.WriteLine("Move {0} From {1} to {2}", n, A, C);
Hanoi(n - 1, B, A, C);
}
}
我们用数量为3个盘子的时候来看一下这个Hanoi(int n, char A, char B, char C)方法
1.Hanoi(n - 1, A, C, B);这个递归是把n-1个盘子按从大到小的顺序放到B柱子上,
也就是n为3-1=2个盘子的时候,即Hanoi(2,A,C,B);
这个时候的B是原来的C,C为原来的B
n>1还要访问Hanoi(n - 1, A, C, B);也就是Hanoi(1,A,C,B);会把A柱子最上边的1盘子放到C柱子上去
n为2 时执行完 Hanoi(n - 1, A, C, B);
Console.WriteLine("Move {0} From {1} to {2}", n, A, C);这是把A柱子上的第2盘子放到B(因为这个时候的C为B)柱子上去
Hanoi(n - 1, B, A, C);这相当于Hanoi(1,C,A,B) 把C柱子上的1盘子放到B上
2 Console.WriteLine("Move {0} From {1} to {2}", n, A, C);
把A柱子上的最后一个盘子3放到C柱子上
到这个时候 A柱子已经空了
B柱子上最小的盘子1在2盘子上边
C柱子上有最大的盘子3
3 Hanoi(n - 1, B, A, C);上一个递归我们已经把n-1个盘子放到了B柱子上,这个方法就是把B柱子上的盘子放到C柱子上
也就是Hanoi(2,B,A,C)它再递归
先调用Hanoi(n - 1, A, C, B); 这个时候 的A是B B为C,C为A 就是把B上的1盘子放到A柱子上
Console.WriteLine("Move {0} From {1} to {2}", n, A, C); 把B柱子上的2盘子放到C柱子上
Hanoi(n - 1, B, A, C);也就是Hanoi(1,A,B,C);会把A柱子上的C盘子入到C柱子上去


