联考day2 C. 舟游
前两天里面的反思里面说最近感觉很颓废,要自己独立解决一道题,于是挑了这一道之前觉得似乎是自己能力之外的题目,逼着自己把每一部分的暴力分都打出来了,但是写完之后感觉难度还是可以接受的。(~~选这道题当然也有假期接触了舟游的可能~~)
题目描述

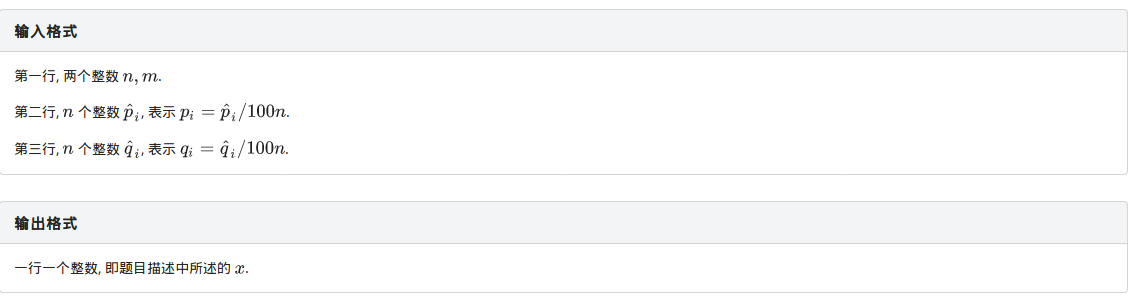
12分解法
我们发现对于每一个干员貌似他从属于哪一个稀有度我们并不在意,我们只想知道抽到他的概率,于是可以把每个稀有度拆为三个干员分开计算。最初经过一番瞎搞我成功得出了错误的转移公式:\(dp[s][i]\)表示当前抽到的卡的状态为\(s\),当前这一次抽卡几经进行了\(i\)轮的期望答案数字。于是有\(dp[s][i]=a_s*dp[s][i+1]+p[k]*dp[s|(1<<(k-1))][i+1]+1\), 同时存在\(dp[s][m]=dp[s][0]+1\),因为这套方程是有问题的,就不再解释了,下面会给出哪里出了问题。发现转移对于每个\(s\)是存在环的,于是对于每个\(s\)都进行一次高斯消元,由于\(s\)的转移要用到\(s|(1<<(k-1))\)于是从大向小枚举,写完后发现样例好像是\((dp[0][0]+1)/2\),于是直接输出,只得到了12pts,(m=1的点)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <iostream>
#define reg register
const int N = 1e6 + 10;
const int Mod = 2e9 + 11;
int read() {
int s = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = (s << 1) + (s << 3) + (ch ^ 48);
ch = getchar();
}
return s * f;
}
typedef long long ll;
ll qpow(ll x, int cnt) {
ll res = 1;
while(cnt) {
if(cnt & 1) res = (res * x) % Mod;
cnt >>= 1;
x = (x * x) % Mod;
}
return res;
}
ll inv(ll x) {
return qpow(x, Mod - 2);
}
int n, m;
ll p[N], q[N], a[N], b[N];
ll calc_p(int t) {
ll res = 0;
for(int j = 1; j <= n * 3; ++j) {
if(!(t & (1 << (j - 1)))) {
res = (res + p[j]) % Mod;
}
}
return (1 - res + Mod) % Mod;
}
ll calc_q(int t) {
ll res = 0;
for(int j = 1; j <= n * 3; ++j) {
if(!(t & (1 << (j - 1)))) {
res = (res + q[j]) % Mod;
}
}
return (1 - res + Mod) % Mod;
}
ll dp[N][65], mp[100][100];
void Init(int id) {
memset(mp, 0, sizeof(mp));
for(int i = 0; i < m - 1; ++i) {
mp[i][i] = 1;
mp[i][m + 1] = 1;
for(int j = 1; j <= n * 3; ++j) {
if((1 << (j - 1)) & id) continue;
int t = (id | (1 << (j - 1)));
mp[i][m + 1] = (mp[i][m + 1] + p[j] * dp[t][i + 1] % Mod) % Mod;
}
mp[i][i + 1] = (Mod - a[id]);
}
mp[m - 1][m - 1] = 1;
mp[m - 1][m + 1] = 1;
for(int j = 1; j <= n * 3; ++j) {
if((1 << (j - 1)) & id) continue;
int t = (id | (1 << (j - 1)));
mp[m - 1][m + 1] = (mp[m - 1][m + 1] + q[j] * dp[t][m] % Mod) % Mod;
}
mp[m - 1][m] = (Mod - b[id]);
mp[m][m] = 1;
mp[m][0] = Mod - 1;
mp[m][m + 1] = 1;
}
void Gauss(int id) {
int now = 0;
for(reg int i = 0; i <= m; ++i) {
int pos = now;
for(reg int j = now + 1; j <= m; ++j) {
if(mp[j][i] > mp[pos][i])
pos = j;
}
if(mp[pos][i] == 0) continue;
if(pos != now) std::swap(mp[pos], mp[now]);
for(reg int j = i + 1; j <= m + 1; ++j) {
mp[now][j] = mp[now][j] * inv(mp[now][i]) % Mod;
}
mp[now][i] = 1;
for(reg int j = now + 1; j <= m; ++j) {
ll cnt = mp[j][i];
for(reg int k = i; k <= m + 1; ++k) {
mp[j][k] = (mp[j][k] - cnt * mp[now][k] % Mod + Mod) % Mod;
}
}
now++;
}
dp[id][m] = mp[m][m + 1];
for(reg int i = m - 1; i >= 0; i--) {
dp[id][i] = mp[i][m + 1];
for(reg int j = i + 1; j <= m; ++j) {
dp[id][i] = (dp[id][i] - mp[i][j] * dp[id][j] % Mod + Mod) % Mod;
}
}
}
int main() {
freopen("arknights.in", "r", stdin);
freopen("arknights.out", "w", stdout);
n = read(); m = read();
for(reg int i = 1; i <= n; ++i) {
int x = read();
for(reg int j = 1; j <= 3; ++j) {
p[(i - 1) * 3 + j] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
}
for(reg int i = 1; i <= n; ++i) {
int x = read();
for(reg int j = 1; j <= 3; ++j) {
q[(i - 1) * 3 + j] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
}
int ed = (1 << (n * 3)) - 1;
for(reg int i = 0; i <= ed; ++i) {
a[i] = calc_p(i);
b[i] = calc_q(i);
}
for(reg int i = ed - 1; i >= 0; --i) {
Init(i);
Gauss(i);
}
printf("%lld\n", (dp[0][0] + 1) * inv(2) % Mod );
return 0;
}
36分解法
12分里面错误的方程是\(dp[s][i]=a_s*dp[s][i+1]+p[k]*dp[s|(1<<(k-1))][i+1]+1\), \(dp[s][m]=dp[s][0]+1\),其中\(a_s\)是提交处理好的前\(m-1\)次抽卡概率为\(p_i\)时状态\(s\)保持不变的概率,代码里面的\(b_i\)同理,只是从\(p_i\)变为了\(q_i\),即第\(m\)次抽卡,\(s\)改变就是抽到了其他的卡,于是乘上一个\(p[k]\)进行转移,一轮抽卡结束之后次数需要加一,于是有了第二个式子。由于这样看上去没有什么问题,但是由于我们的定义是当前抽卡一轮里面已经抽了\(i\)次还需要的期望次数,于是第一个式子里面最后的\(1\)是多余的,因为它们都是在同一次抽卡的过程中出现的状态,我们只需要在每次抽卡结束,即第\(m\)次结束之后给它加一个\(1\)就行了,所以第二个式子是没有问题的。把式子改正,可以得到最暴力的36分。这里解释一下为什么输出\(dp[0][m]\)而不是\(dp[0][0]\),从我们的定义入手,\(dp[0][0]\)表示的是当前啥也没有新的抽卡一轮刚刚开始已经抽了\(0\)次还需要的期望次数。当前这一轮刚刚开始,转移一定是不完整的。于是我们选择抽完了一轮\(m\)次还需要的期望次数作为答案,此时新的一轮还未开始,而且手中没有任何卡,可以认为是初态。时间复杂度大概为\(m^3*2^{3m}\)。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <iostream>
#define reg register
const int N = 1e6 + 10;
const int Mod = 2e9 + 11;
int read() {
int s = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = (s << 1) + (s << 3) + (ch ^ 48);
ch = getchar();
}
return s * f;
}
typedef long long ll;
ll qpow(ll x, int cnt) {
ll res = 1;
while(cnt) {
if(cnt & 1) res = (res * x) % Mod;
cnt >>= 1;
x = (x * x) % Mod;
}
return res;
}
ll inv(ll x) {
return qpow(x, Mod - 2);
}
int n, m;
ll p[N], q[N], a[N], b[N];
ll calc_p(int t) { //处理状态为t时的前m-1次抽卡状态不变的概率。
ll res = 0;
for(int j = 1; j <= n * 3; ++j) {
if(!(t & (1 << (j - 1)))) {
res = (res + p[j]) % Mod;
}
}
return (1 - res + Mod) % Mod;
}
ll calc_q(int t) { //处理状态为t时的第m次抽卡状态不变的概率。
ll res = 0;
for(int j = 1; j <= n * 3; ++j) {
if(!(t & (1 << (j - 1)))) {
res = (res + q[j]) % Mod;
}
}
return (1 - res + Mod) % Mod;
}
ll dp[N][65], mp[100][100];
void Init(int id) { //初始化矩阵
memset(mp, 0, sizeof(mp));
for(int i = 0; i < m - 1; ++i) {
mp[i][i] = 1;
for(int j = 1; j <= n * 3; ++j) {
if((1 << (j - 1)) & id) continue;
int t = (id | (1 << (j - 1))); //枚举所有抽到状态之外的卡的概率。
mp[i][m + 1] = (mp[i][m + 1] + p[j] * dp[t][i + 1] % Mod) % Mod;
}
mp[i][i + 1] = (Mod - a[id]); //这一次什么也没抽到,状态不变,从次数加一的方向转移。
}
mp[m - 1][m - 1] = 1;
for(int j = 1; j <= n * 3; ++j) { //同上
if((1 << (j - 1)) & id) continue;
int t = (id | (1 << (j - 1)));
mp[m - 1][m + 1] = (mp[m - 1][m + 1] + q[j] * dp[t][m] % Mod) % Mod;
}
mp[m - 1][m] = (Mod - b[id]);
mp[m][m] = 1; //第二个式子的初始化
mp[m][0] = Mod - 1;
mp[m][m + 1] = 1;
}
void Gauss(int id) { //常规高斯消元
int now = 0;
for(reg int i = 0; i <= m; ++i) {
int pos = now;
for(reg int j = now + 1; j <= m; ++j) {
if(mp[j][i] > mp[pos][i])
pos = j;
}
if(mp[pos][i] == 0) continue;
if(pos != now) std::swap(mp[pos], mp[now]);
for(reg int j = i + 1; j <= m + 1; ++j) {
mp[now][j] = mp[now][j] * inv(mp[now][i]) % Mod;
}
mp[now][i] = 1;
for(reg int j = now + 1; j <= m; ++j) {
ll cnt = mp[j][i];
for(reg int k = i; k <= m + 1; ++k) {
mp[j][k] = (mp[j][k] - cnt * mp[now][k] % Mod + Mod) % Mod;
}
}
now++;
}
dp[id][m] = mp[m][m + 1];
for(reg int i = m - 1; i >= 0; i--) {
dp[id][i] = mp[i][m + 1];
for(reg int j = i + 1; j <= m; ++j) {
dp[id][i] = (dp[id][i] - mp[i][j] * dp[id][j] % Mod + Mod) % Mod;
}
}
}
int main() {
freopen("arknights.in", "r", stdin);
freopen("arknights.out", "w", stdout);
n = read(); m = read();
for(reg int i = 1; i <= n; ++i) {
int x = read();
for(reg int j = 1; j <= 3; ++j) { //注意三个人的概率要处以3
p[(i - 1) * 3 + j] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
}
for(reg int i = 1; i <= n; ++i) {
int x = read();
for(reg int j = 1; j <= 3; ++j) {
q[(i - 1) * 3 + j] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
}
int ed = (1 << (n * 3)) - 1;
for(reg int i = 0; i <= ed; ++i) {
a[i] = calc_p(i);
b[i] = calc_q(i);
}
for(reg int i = ed - 1; i >= 0; --i) { //从大到小依次运算
Init(i);
Gauss(i);
}
printf("%lld\n", dp[0][m]);
return 0;
}
60~76分解法
至于为什么会有这个分数范围我也挺懵,学长讲题的时候提到这样写大概可以得到60分,其他的会超时,但我写完之后直接得了76分,可能是register和快读的功劳吧...
在12分的做法里面我们提到把一个稀有度的三个干员拆开单独计算,但是其实他们都是一样的,我们可以对于每一个稀有度只记录我们在这个稀有度里面抽到了几个人就可以了,但是我们一般的装压似乎只能记录\(0\),\(1\)两个状态,多出的状态\(3\)似乎没有方法记录,但是我们用两个二进制位来记录状态不就行了嘛。对于每一个稀有度的已经获得的人数就可以表示了,这样代替36分里面的将3个人拆开的做法,时间复杂度优化至了\(m^3*2^{2m}\),可以取得60分的好成绩。
现在解释一下代码里面频繁出现的\(tim=((t\&(1<<(j)))!=0)\),\(tim=(tim<<1)+((t\&(1<<(j-1)))!=0)\)是个什么东西,这样我们可以从状态\(t\)里面取出稀有度为\(j\)的干员已经抽到的数量,代替之前里面的二进制运算。
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <iostream>
#define reg register
const int N = (2 << 20);
const int Mod = 2e9 + 11;
int read() {
int s = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = (s << 1) + (s << 3) + (ch ^ 48);
ch = getchar();
}
return s * f;
}
typedef long long ll;
ll qpow(ll x, int cnt) {
ll res = 1;
while(cnt) {
if(cnt & 1) res = (res * x) % Mod;
cnt >>= 1;
x = (x * x) % Mod;
}
return res;
}
ll inv(ll x) {
return qpow(x, Mod - 2);
}
int n, m;
ll p[N], q[N], a[N], b[N];
ll calc_p(int t) {
ll res = 0;
for(int j = 1; j <= n * 2; j += 2) { //由于状态变化,初始化方式也有所变化
ll tim = 0;
tim = ((t & (1 << (j))) != 0);
tim = (tim << 1) + ((t & (1 << (j - 1))) != 0);
res = (res + (3 - tim) * p[(j + 1) / 2] % Mod) % Mod;
}
return (1 - res + Mod) % Mod;
}
ll calc_q(int t) {
ll res = 0;
for(int j = 1; j <= n * 2; j += 2) {
ll tim = 0;
tim = ((t & (1 << (j))) != 0);
tim = (tim << 1) + ((t & (1 << (j - 1))) != 0);
res = (res + (3 - tim) * q[(j + 1) / 2] % Mod) % Mod;
}
return (1 - res + Mod) % Mod;
}
ll dp[N][65], mp[100][100];
void Init(int id) {
memset(mp, 0, sizeof(mp));
for(reg int i = 0; i < m - 1; ++i) {
mp[i][i] = 1;
for(reg int j = 1; j <= n * 2; j += 2) {
if(((1 << (j - 1)) & id) && ((1 << j) & id)) continue;
reg int tim = ((id & (1 << (j))) != 0);
tim = (tim << 1) + ((id & (1 << (j - 1))) != 0);
tim = 3 - tim; //由于两个二进制位表示一个稀有度,相应的下标为(j+1)/2
mp[i][m + 1] = (mp[i][m + 1] + tim * p[(j + 1) / 2] % Mod * dp[id + (1 << (j - 1))][i + 1] % Mod) % Mod;
}
mp[i][i + 1] = (Mod - a[id]);
}
mp[m - 1][m - 1] = 1;
for(reg int j = 1; j <= n * 2; j += 2) {
if(((1 << (j - 1)) & id) && ((1 << j) & id)) continue;
reg int tim = ((id & (1 << (j))) != 0);
tim = (tim << 1) + ((id & (1 << (j - 1))) != 0);//同上
tim = 3 - tim;
mp[m - 1][m + 1] = (mp[m - 1][m + 1] + tim * q[(j + 1) / 2] % Mod * dp[id + (1 << (j - 1))][m] % Mod) % Mod;
}
mp[m - 1][m] = (Mod - b[id]);
mp[m][m] = 1;
mp[m][0] = Mod - 1;
mp[m][m + 1] = 1;
}
int t = 0;
void Gauss(int id) {
int now = 0;
for(reg int i = 0; i <= m; ++i) {
int pos = now;
for(reg int j = now + 1; j <= m; ++j) {
if(mp[j][i] > mp[pos][i])
pos = j;
}
if(mp[pos][i] == 0) continue;
if(pos != now) std::swap(mp[pos], mp[now]);
for(reg int j = i + 1; j <= m + 1; ++j) {
mp[now][j] = mp[now][j] * inv(mp[now][i]) % Mod;
}
mp[now][i] = 1;
for(reg int j = now + 1; j <= m; ++j) {
ll cnt = mp[j][i];
for(reg int k = i; k <= m + 1; ++k) {
mp[j][k] = (mp[j][k] - cnt * mp[now][k] % Mod + Mod) % Mod;
}
}
now++;
}
dp[id][m] = mp[m][m + 1];
for(reg int i = m - 1; i >= 0; i--) {
dp[id][i] = mp[i][m + 1];
for(reg int j = i + 1; j <= m; ++j) {
dp[id][i] = (dp[id][i] - mp[i][j] * dp[id][j] % Mod + Mod) % Mod;
}
}
}
int main() {
//freopen("a.in", "r", stdin);
freopen("arknights.in", "r", stdin);
freopen("arknights.out", "w", stdout);
n = read(); m = read();
for(reg int i = 1; i <= n; ++i) {
int x = read();
p[i] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
for(reg int i = 1; i <= n; ++i) {
int x = read();
q[i] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
int ed = (1 << (n * 2)) - 1;
//注意终态ed也发生了变化
for(reg int i = 0; i <= ed; ++i) {
a[i] = calc_p(i);
b[i] = calc_q(i);
}
for(reg int i = ed - 1; i >= 0; --i) {
Init(i);
Gauss(i);
}
printf("%lld\n", dp[0][m]);
return 0;
}
76~84分解法
从60分的解法里面我们可以得到启发,可以把相等稀有度的干员合并起来一起计算。而特殊性质里面正好给了我们所有干员都一样的情况,对于这种情况我们可以直接放弃装压。由于干员全部一样我们直接记录已经抽到了几个就行了,我们就不用再从终态枚举到\(0\)依次进行运算了,但是注意干员总数是\(n*3\),在进行运算的时候记得乘上。时间复杂度为\((n*3)*m^3\)可以拿到部分分16~8分(如果你在60分的算法里面得到了76分的话就只剩8分了...),跑的比前面的快了\(20\)来倍...(图中下面的是特殊情况)

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <iostream>
#define reg register
const int N = (2 << 20);
const int Mod = 2e9 + 11;
int read() {
int s = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = (s << 1) + (s << 3) + (ch ^ 48);
ch = getchar();
}
return s * f;
}
typedef long long ll;
ll qpow(ll x, int cnt) {
ll res = 1;
while(cnt) {
if(cnt & 1) res = (res * x) % Mod;
cnt >>= 1;
x = (x * x) % Mod;
}
return res;
}
ll inv(ll x) {
return qpow(x, Mod - 2);
}
int n, m;
ll p[N], q[N], a[N], b[N];
ll calc_p(int t) {
ll res = 0;
for(int j = 1; j <= n * 2; j += 2) {
ll tim = 0;
tim = ((t & (1 << (j))) != 0);
tim = (tim << 1) + ((t & (1 << (j - 1))) != 0);
res = (res + (3 - tim) * p[(j + 1) / 2] % Mod) % Mod;
}
return (1 - res + Mod) % Mod;
}
ll calc_q(int t) {
ll res = 0;
for(int j = 1; j <= n * 2; j += 2) {
ll tim = 0;
tim = ((t & (1 << (j))) != 0);
tim = (tim << 1) + ((t & (1 << (j - 1))) != 0);
res = (res + (3 - tim) * q[(j + 1) / 2] % Mod) % Mod;
}
return (1 - res + Mod) % Mod;
}
ll dp[N][65], mp[100][100];
void Init(int id) {
memset(mp, 0, sizeof(mp));
for(reg int i = 0; i < m - 1; ++i) {
mp[i][i] = 1;
for(reg int j = 1; j <= n * 2; j += 2) {
if(((1 << (j - 1)) & id) && ((1 << j) & id)) continue;
reg int tim = ((id & (1 << (j))) != 0);
tim = (tim << 1) + ((id & (1 << (j - 1))) != 0);
tim = 3 - tim;
mp[i][m + 1] = (mp[i][m + 1] + tim * p[(j + 1) / 2] % Mod * dp[id + (1 << (j - 1))][i + 1] % Mod) % Mod;
}
mp[i][i + 1] = (Mod - a[id]);
}
mp[m - 1][m - 1] = 1;
for(reg int j = 1; j <= n * 2; j += 2) {
if(((1 << (j - 1)) & id) && ((1 << j) & id)) continue;
reg int tim = ((id & (1 << (j))) != 0);
tim = (tim << 1) + ((id & (1 << (j - 1))) != 0);
tim = 3 - tim;
mp[m - 1][m + 1] = (mp[m - 1][m + 1] + tim * q[(j + 1) / 2] % Mod * dp[id + (1 << (j - 1))][m] % Mod) % Mod;
}
mp[m - 1][m] = (Mod - b[id]);
mp[m][m] = 1;
mp[m][0] = Mod - 1;
mp[m][m + 1] = 1;
}
int t = 0;
void Gauss(int id) {
int now = 0;
for(reg int i = 0; i <= m; ++i) {
int pos = now;
for(reg int j = now + 1; j <= m; ++j) {
if(mp[j][i] > mp[pos][i])
pos = j;
}
if(mp[pos][i] == 0) continue;
if(pos != now) std::swap(mp[pos], mp[now]);
for(reg int j = i + 1; j <= m + 1; ++j) {
mp[now][j] = mp[now][j] * inv(mp[now][i]) % Mod;
}
mp[now][i] = 1;
for(reg int j = now + 1; j <= m; ++j) {
ll cnt = mp[j][i];
for(reg int k = i; k <= m + 1; ++k) {
mp[j][k] = (mp[j][k] - cnt * mp[now][k] % Mod + Mod) % Mod;
}
}
now++;
}
dp[id][m] = mp[m][m + 1];
for(reg int i = m - 1; i >= 0; i--) {
dp[id][i] = mp[i][m + 1];
for(reg int j = i + 1; j <= m; ++j) {
dp[id][i] = (dp[id][i] - mp[i][j] * dp[id][j] % Mod + Mod) % Mod;
}
}
}
void Init_cheat(int id) { //为特殊性质准备的特殊矩阵初始化
memset(mp, 0, sizeof(mp));
for(reg int i = 0; i < m - 1; ++i) { //此时的id已经不是状压,而是当前抽到的干员数量
mp[i][i] = 1;
mp[i][m + 1] = (mp[i][m + 1] + (n - id) * p[1] % Mod * dp[id + 1][i + 1] % Mod) % Mod;
mp[i][i + 1] = (Mod - (1 - p[1] * (n - id) % Mod + Mod) % Mod) % Mod;
}
mp[m - 1][m - 1] = 1; //因为干员都一样,省去了枚举下一次抽到那一个的过程,直接从id+1的方向进行转移就行了.
mp[m - 1][m + 1] = (mp[m - 1][m + 1] + (n - id) * q[1] % Mod * dp[id + 1][m] % Mod) % Mod;
mp[m - 1][m] = (Mod - (1 - q[1] * (n - id) % Mod + Mod) % Mod) % Mod;
mp[m][m] = 1;
mp[m][0] = Mod - 1;
mp[m][m + 1] = 1;
}
int main() {
//freopen("a.in", "r", stdin);
freopen("arknights.in", "r", stdin);
freopen("arknights.out", "w", stdout);
bool flag = 1;
n = read(); m = read();
for(reg int i = 1; i <= n; ++i) {
int x = read();
p[i] = x * inv(100 * n) % Mod * inv(3) % Mod;
if(i != 1 && p[i] != p[i - 1]) flag = 0; //判断是不是特殊情况
}
for(reg int i = 1; i <= n; ++i) {
int x = read();
q[i] = x * inv(100 * n) % Mod * inv(3) % Mod;
if(i != 1 && q[i] != q[i - 1]) flag = 0;
}
if(flag) {
n *= 3; //千万记得n要乘以三
for(reg int i = n - 1; i >= 0; --i) {
Init_cheat(i);
Gauss(i);
}
printf("%lld\n", dp[0][m]);
return 0;
}
int ed = (1 << (n * 2)) - 1;
for(reg int i = 0; i <= ed; ++i) {
a[i] = calc_p(i);
b[i] = calc_q(i);
}
for(reg int i = ed - 1; i >= 0; --i) {
Init(i);
Gauss(i);
}
printf("%lld\n", dp[0][m]);
return 0;
}
100分做法
其实在写上面的解法的过程中你就会发现,貌似60分里面的\(dp[s][i]\)需要消掉的未知变量只有\(dp[s][i+1]\)其他的由于倒着枚举的缘故都可以算作常数放入矩阵,于是你把初始化出来的矩阵打印出来会发现一个神奇的矩阵:
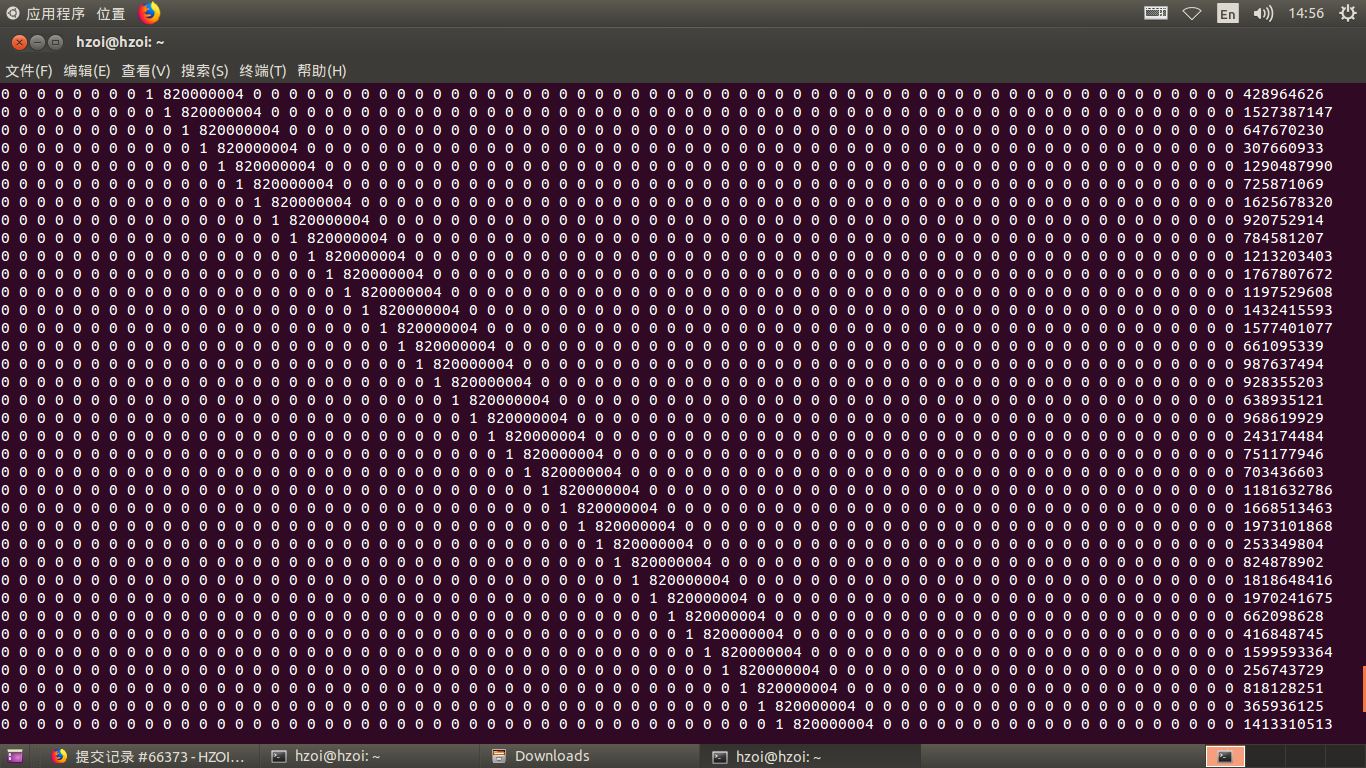
我们每一次的转移都只和下一次的状态有关,其实它就是一个链首尾相接形成的一个大环,于是我们可以手动模拟高斯消元,用\(O(n)\)的时间解出答案。从60分做法里面我们可以得到,\(dp[s][i]=a_s*dp[s][i+1]+p[k]*dp[s|(1<<(k-1))][i+1]\),其中\(dp[s|(1<<(k-1))][i+1]\)和\(p[k]\)已知,我们就可以改写为\(dp[s][i]=a_i*dp[s][i+1]+b_i\), 特别的,对于\(i=m-1\)存在\(dp[s][m-1]=a_{m-1}*dp[s][m]+b_{m-1}\),同理有\(dp[s][m-2]=a_x*dp[s][m-1]+b_x\), 发现把前面的式子带入后面的式子,\(dp[s][m-2]\)也可以写为\(dp[s][m-2]=a_{m-2}*dp[s][m]+b_{m-2}\)以此类推,最后可以得到\(dp[s][0]=a_{0}*dp[s][m]+b_{0}\),而我们同时又有\(dp[s][m]=dp[s][0]+1\), 把该式带入前面,可以得到\(dp[s][0]=(a_0+b_0)/(1-a_0)\), 于是可以得到\(dp[s][0]\)和\(dp[s][m]\),将\(dp[s][m]\)带回\(dp[s][k]=a_{k}*dp[s][m]+b_{k}\)可以解得\(dp[s][k]\)这道题就做完了。此时时间复杂度为\(m*2^{2*n}\), 可以通过该题.(代码之中由于a, b数组我已经用了,用的是aa和bb)
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <bitset>
#include <iostream>
#define reg register
#define debug puts("-debug-")
const int N = (2 << 20);
const int Mod = 2e9 + 11;
int read() {
int s = 0, f = 1;
char ch = getchar();
while(ch < '0' || ch > '9') {
if(ch == '-') f = -1;
ch = getchar();
}
while(ch >= '0' && ch <= '9') {
s = (s << 1) + (s << 3) + (ch ^ 48);
ch = getchar();
}
return s * f;
}
typedef long long ll;
ll qpow(ll x, int cnt) {
ll res = 1;
while(cnt) {
if(cnt & 1) res = (res * x) % Mod;
cnt >>= 1;
x = (x * x) % Mod;
}
return res;
}
ll inv(ll x) {
return qpow(x, Mod - 2);
}
int n, m;
ll p[N], q[N], a[N], b[N];
ll calc_p(int t) {
ll res = 0;
for(int j = 1; j <= n * 2; j += 2) {
ll tim = 0;
tim = ((t & (1 << (j))) != 0);
tim = (tim << 1) + ((t & (1 << (j - 1))) != 0);
res = (res + (3 - tim) * p[(j + 1) / 2] % Mod) % Mod;
}
return (1 - res + Mod) % Mod;
}
ll calc_q(int t) {
ll res = 0;
for(int j = 1; j <= n * 2; j += 2) {
ll tim = 0;
tim = ((t & (1 << (j))) != 0);
tim = (tim << 1) + ((t & (1 << (j - 1))) != 0);
res = (res + (3 - tim) * q[(j + 1) / 2] % Mod) % Mod;
}
return (1 - res + Mod) % Mod;
}
ll dp[N][65], aa[100], bb[100];
void Init(int id) { //这里不再是初始化矩阵,而是初始化aa, bb数组.
memset(aa, 0, sizeof(aa));
memset(bb, 0, sizeof(bb));
for(reg int j = 1; j <= n * 2; j += 2) {
if(((1 << (j - 1)) & id) && ((1 << j) & id)) continue;
reg int tim = ((id & (1 << (j))) != 0);
tim = (tim << 1) + ((id & (1 << (j - 1))) != 0);
tim = 3 - tim; //仿照60分做法计算转移系数
bb[m - 1] = (bb[m - 1] + tim * q[(j + 1) / 2] % Mod * dp[id + (1 << (j - 1))][m] % Mod) % Mod;
}
aa[m - 1] = b[id];//不变的可能
for(reg int i = m - 2; i >= 0; --i) {
aa[i] = aa[i + 1] * a[id] % Mod; //要乘的话两个数组都要乘, 通过上面的式子带入不难得知.
bb[i] = bb[i + 1] * a[id] % Mod;
for(reg int j = 1; j <= n * 2; j += 2) {
if(((1 << (j - 1)) & id) && ((1 << j) & id)) continue;
reg int tim = ((id & (1 << (j))) != 0);
tim = (tim << 1) + ((id & (1 << (j - 1))) != 0);
tim = 3 - tim;
bb[i] = (bb[i] + tim * p[(j + 1) / 2] % Mod * dp[id + (1 << (j - 1))][i + 1] % Mod) % Mod;
}
}
}
void Gauss(int id) {
dp[id][0] = (aa[0] + bb[0]) % Mod * inv((Mod + 1 - aa[0]) % Mod) % Mod; //dp[id][0]可以直接计算
dp[id][m] = (dp[id][0] + 1) % Mod;
for(int i = m - 1; i; --i) { //回代, 计算dp[id][k]
dp[id][i] = (aa[i] * dp[id][m] % Mod + bb[i]) % Mod;
}
}
int main() {
freopen("arknights.in", "r", stdin);
freopen("arknights.out", "w", stdout);
n = read(); m = read();
for(reg int i = 1; i <= n; ++i) {
int x = read();
p[i] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
for(reg int i = 1; i <= n; ++i) {
int x = read();
q[i] = x * inv(100 * n) % Mod * inv(3) % Mod;
}
int ed = (1 << (n * 2)) - 1;
for(reg int i = 0; i <= ed; ++i) {
a[i] = calc_p(i);
b[i] = calc_q(i);
}
for(reg int i = ed - 1; i >= 0; --i) {
Init(i);
Gauss(i);
}
printf("%lld\n", dp[0][m]);
return 0;
}
这题还有一个加强版,这份代码就过不去了,有需要的可自行问学长方法......
现在感觉自己越来越菜了,考试一直考不好,也很郁闷,距离CSP也没几天了,我这个状态还需要尽快调整.这次把这到题彻彻底底的弄懂给自己的信心加成还是有的,以后的一些好题也一定要好好改,不要让之前反思里面的话成为空词...现在我的危机还是挺严重的,眼看就要掉出一机房,与别人的差距越来越大.考试心态,考试策略出现问题,发挥屡次不好。但是我还是希望可以通过剩下不多的时间提升自己。绝对不能让自己的OI生涯到次为止,加油吧!



