柱、锥、台、球的体积公式推导(不用积分)
求这些规则几何体的体积如果都要算积分的话,那也太麻烦了。本文将讨论如何不用积分就能得出结论。
虽然不用算积分,但也要用到积分的思想。因此本文承认以下引理:
引理 (袓暅原理) 所有等高处横截面积相等的两个同高立体的体积相等
柱体
对某一柱体,构造与之具有相同的底面积和高的正四棱柱,则由引理可知,该柱体与构造出的正四棱柱具有相同的体积。又因为正四棱柱的体积等于底面积乘以高,所以该柱体的体积即为底面积乘以高。由此可得任意柱体的体积都是底面积乘以高,即:
\( V_{柱}=Sh \)
锥体
对某一锥体,构造与之具有相同的底面积和高的斜三棱锥,并要求它的底面是等腰直角三角形,且直角顶点与该斜三棱锥的顶点之间的那一条棱与底面垂直。(此几何体俗称「墙角」)
由引理可知,原锥体的体积与构造出的「墙角」具有相同的体积。下证「墙角」的体积是底与高乘积的三分之一。
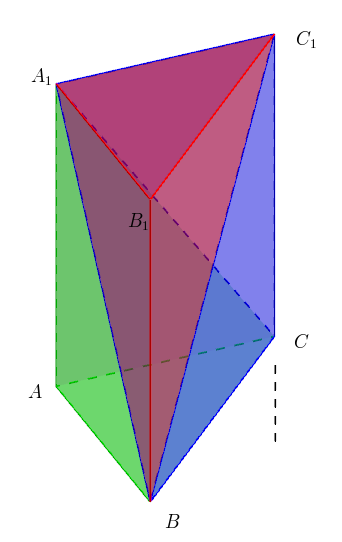
如图,绿色的 \(A_{1}-ABC\) 即为「墙角」,\(\angle{BAC}=90^{\circ}\), \(AA_1 \perp 面ABC\). 把它补成直三棱柱 \(ABC-A_{1}B_{1}C_{1}\), 连接 \(BC_1\).
此时这个直三棱柱被分成了三个部分,即 \(A_{1}-ABC\), \(A_{1}-BB_{1}C_{1}\) 和 \(A_{1}-BCC_1\), 它们的体积和即为该直三棱柱的体积。
因为等底等高的三棱锥体积相等(由引理 1 及截面和底面的相似性易知),且三棱锥可以把任一面当作底面,所以有
\( V_{A_{1}-BB_{1}C_{1}} = V_{C_{1}-A_{1}B_{1}B} = V_{C_{1}-A_{1}AB} \)
以及
\( V_{A_{1}-BB_{1}C_{1}} = V_{A_{1}-BCC_{1}} \)
综合两式得
\( V_{C_{1}-A_{1}AB} = V_{A_{1}-BB_{1}C_{1}} = V_{A_{1}-BCC_{1}} \)
即这三个三棱锥具有相同的体积,又因为它们的体积之和即为直三棱柱的体积,所以「墙角」的体积就是直三棱柱体积的三分之一。
由直三棱柱的体积等于底面积乘以高可知,「墙角」的体积就是底乘高的三分之一。
所以,原锥体的体积即为底乘高的三分之一,即:
\( V_{锥}=\frac{1}{3}Sh \)
台体
把台体补成锥体,这样就出现了一大一小两个锥体,台体的体积可以看成是大的锥体的体积减去小的锥体的体积,即:
\( V_{台} = V_{大锥} - V_{小锥} \)
\( V_{台} = \frac{1}{3}\left ( S_{下}h_{大} - S_{上}h_{小} \right ) \) (1)
根据截面和底面的相似性可知
\( \frac{h_{小}}{h_{大}} = \sqrt{\frac{S_{上}}{S_{下}}} \)
\( h_{小} = \sqrt{\frac{S_{上}}{S_{下}}}h_{大} \) (2)
\( h = h_{大} - h_{小} = \left ( 1-\sqrt{\frac{S_{上}}{S_{下}}} \right )\cdot h_{大} \)
\( h_{大} = \frac{h}{1-\sqrt{\frac{S_{上}}{S_{下}}}} \) (3)
将 (2) 代入 (1) 式得
\( V_{台} = \frac{1}{3}\left ( S_{下}\sqrt{\frac{S_{下}}{S_{上}}}h_{小} - S_{上}h_{小} \right ) \)
\( V_{台} = \frac{1}{3}h_{大}\left ( S_{下} - S_{上}\sqrt{\frac{S_{上}}{S_{下}}} \right ) \)
再代入 (3) 得
\( V_{台} = \frac{1}{3}\frac{h}{1-\sqrt{\frac{S_{上}}{S_{下}}}}\left ( S_{下} - S_{上}\sqrt{\frac{S_{上}}{S_{下}}} \right ) \)
\( V_{台} = \frac{1}{3}h\left ( \frac{\sqrt{S_{下}}S_{下}}{\sqrt{S_{下}}-\sqrt{S_{上}}}-\frac{\sqrt{S_{上}}S_{上}}{\sqrt{S_{下}}-\sqrt{S_{上}}} \right ) \)
\( V_{台} = \frac{1}{3}h\left ( \frac{(\sqrt{S_{下}}S_{下}-\sqrt{S_{上}}S_{上})(\sqrt{S_{下}}+\sqrt{S_{上}})}{S_{下}-S_{上}} \right ) \)
\( V_{台} = \frac{1}{3}h\left ( \frac{S_{下}^2-S_{上}^2+\sqrt{S_{上}S_{下}}(S_{下}-S_{上})}{S_{下}-S_{上}} \right ) \)
\( V_{台} = \frac{1}{3}h\left ( S_{上}+\sqrt{S_{上}S_{下}}+S_{下} \right ) \)
球体
按照之前的思路应用引理,寻找截面积与球处处相等的目前已经可以求出体积的几何体。
考察半径为 \(R\) 的球在距球心高 \(h\) 处的截面积 \(S\).
由勾股定理知,高 \(h\) 处的小圆半径为 \( r = \sqrt{R^2-h^2} \).
所以
\( S = \pi r^2 \)
\( S = \pi \left( R^2-h^2 \right ) \)
\( S = \pi R^2 - \pi h^2 \)
观察这个式子,\(R\) 是常数,\(h\) 在变化,容易得出结论:所需构造的等积几何体即是球的外接圆柱除去中心在球心顶角为直角的圆锥的部分。
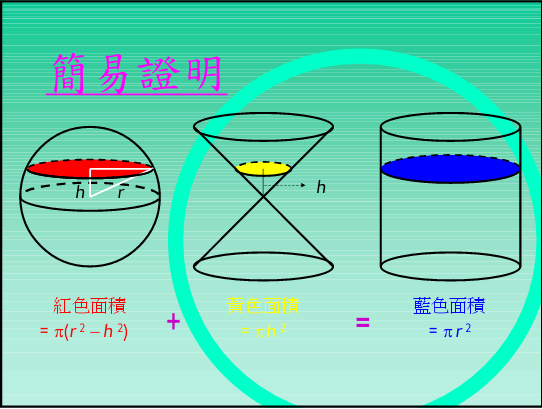
(图片来自 Slide 《球體面積和體積》)
由此立得
\( V_{球} = \pi R^2\cdot(2R) - \frac{1}{3} \pi R^2\cdot(2R) \)
\( V_{球} = \frac{2}{3} \cdot \pi \cdot 2R^3 \)
\( V_{球} = \frac{4}{3} \pi R^3 \)



