抛物线的几何性质(传统几何法推导)
抛物线有很多几何性质,网上也有不少关于这些性质的推导的文章,不过几乎清一色地都是用的解析几何的方法。联立方程,导出根与系数的关系,算算算算算……
但是,与同样是二次曲线的椭圆和双曲线不同,圆和抛物线的几何性质非常「好」,不用坐标法,也能推出很多结论。不过相比具有完美对称性的圆来说,抛物线还是逊色了许多。圆的切线很容易用几何条件去描述(容易用反证法证出圆的切线垂直于过切点的直径),而抛物线的切线虽然也容易用几何条件描述,但相关结论却难以用纯几何法证出。所以涉及切线问题时,还是需要用坐标法证明一个重要结论的。虽然如此,本文的证明过程还是要比带着一大坨方程的纯代数法清爽得多。
要证结论,得先给出定义:
定义 由平面内到一个定点和一条定直线距离相等的所有点构成的图形,称为抛物线. 定点称为抛物线的焦点,定直线称为抛物线的准线, 焦点到准线的距离称为焦准距.
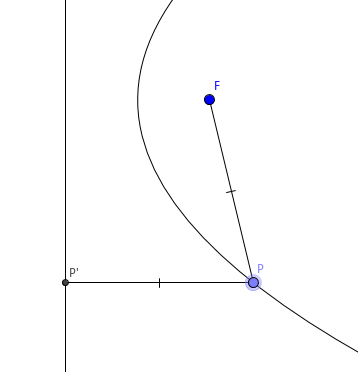
结论 1 抛物线是轴对称图形,准线过焦点的垂线是它的一条对称轴.
证明
设焦点为 \(F\), 准线为 \(l\), 轴为 \(a\), 抛物线上有一点 \(P\). 过 \(P\) 作 \(PP'\perp l\), 垂足为 \(P'\). 当 \(P\) 不在 \(a\) 上时,作 \(P\) 关于 \(a\) 的对称点 \(Q\), 作 \(P'\) 关于 \(a\) 的对称点 \(Q'\). 连接 \(FP\)、\(FQ\). 由 \(a \perp l\) 知 \( PP'\parallel a \), 所以 \( QQ'\parallel a \), 所以 \(QQ' \perp l\). 由对称知 \(PP'=QQ'\), \(FP=FQ\), 又 \( FP=PP' \), 所以 \( FQ=QQ' \), 所以 \(Q\) 在抛物线上, 结论得证.
定义 抛物线的准线过焦点的垂线称为抛物线的轴, 轴与抛物线的交点称为抛物线的顶点.
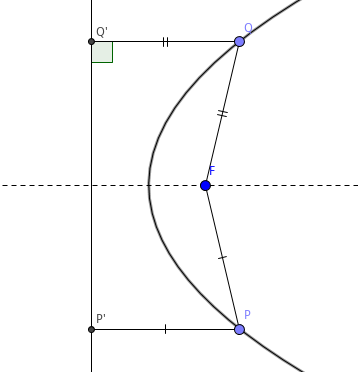
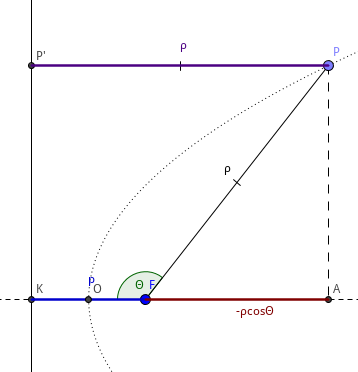
结论 2 设抛物线的焦点为 \(F\), 顶点为 \(O\), 焦准距为 \(p\), 对于抛物线上任意一点 \(P\), \(FP = \frac{p}{1+\cos{\angle{OFP}}}\).
证明
设 \(FP=\rho\), \(\angle{OFP}=\theta\).
如图,当 \(\theta > 90^{\circ}\) 时,作 \(FP\) 在轴上的投影,易得 \(\rho = p-\rho\cos{\theta}\). 整理得 \(\rho = \frac{p}{1+\cos{\theta}}\), 即 \(FP = \frac{p}{1+\cos{\angle{OFP}}}\).
同理可证当 \(0^{\circ} < \theta < 90^{\circ}\) 时,结论仍然成立.
当 \(\theta = 90^{\circ}\) 时,\( PF=p \), 结论仍然成立。
当 \(\theta = 0^{\circ}\) 时,\( PF = \frac{p}{2} \), 结论仍然成立.
综上,对于抛物线上任意一点 \(P\), 结论成立.
推论 1 设抛物线的焦准距为 \(p\), 过抛物线焦点 \(F\) 的直线与抛物线交于 \(A\)、\(B\) 两点,则有 \(\frac{1}{AF}+\frac{1}{BF}=\frac{2}{p}\).
推论 2 设抛物线的顶点为 \(O\), 焦准距为 \(p\), \(\angle{OFP}=\theta\), 过抛物线焦点 \(F\) 的直线与抛物线交于 \(A\)、\(B\) 两点,则有 \(AB=\frac{2p}{\sin^2{\theta}}\).
结论 3 设抛物线轴与准线的交点为 \(K\), 过抛物线焦点 \(F\) 的直线与抛物线交于 \(A\)、\(B\) 两点, 则轴平分 \(\angle{AKB}\).
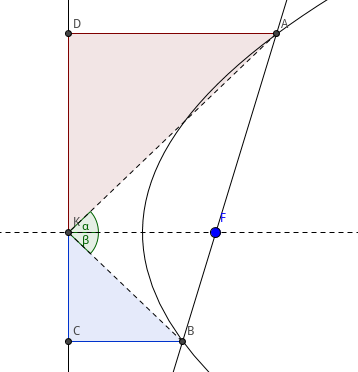
如图,设准线为 \(l\), 轴为 \(a\), 过 \(A\) 作 \(AD\perp l\), 交 \(l\) 于 \(D\), 过 B 作 \(BC\perp l\), 交 \(l\) 于 \(C\).
\(\because\) \(AD\perp l\) 且 \(BC\perp l\)
\(\therefore\) \(AD\parallel a\) 且 \(BC\parallel a\)
\(\therefore\) \(\frac{KD}{KC}=\frac{FA}{FB} \)
又 \(\because\) \(FA=AD\) 且 \(FB=BC\)
\(\therefore\) \(\frac{KD}{KC}=\frac{AD}{BC} \)
\(\therefore\) \(\triangle{KDA}\sim \triangle{KCB}\)
\(\therefore\) \(\angle{DKA} = \angle{CKB}\)
\(\therefore\) 轴平分 \(\angle{AKB}\)
结论 4 设抛物线焦点为 \(F\), 准线为 \(l\), 轴与准线的交点为 \(K\), 过 \(F\) 的直线与抛物线交于 \(A\)、\(B\) 两点,过 \(A\) 作 \(AD\perp l\), 交 \(l\) 于 \(D\), 过 B 作 \(BC\perp l\), 交 \(l\) 于 \(C\), 则\(FD\) 平分 \(\angle{KFA}\), \(FC\) 平分 \(\angle{KFB}\), \(FC\perp FD\).

证明
\(\because\) \(FB=BC\), \(FA=AD\)
\(\therefore\) \(\angle{AFD}=\angle{ADF}\), \(\angle{BFC}=\angle{BCF}\)
\(\because\) \(KF\parallel AD\), \(KF\parallel BC\)
\(\therefore\) \(\angle{KFD}=\angle{ADF}\), \(\angle{KFC}=\angle{FCB}\)
\(\therefore\) \(FD\) 平分 \(\angle{KFA}\), \(FC\) 平分 \(\angle{KFB}\)
\(\therefore\) \(FC\perp FD\)
结论 5 设抛物线焦点为 \(F\), 准线为 \(l\), 顶点为 \(O\), 过 \(F\) 的直线与抛物线交于 \(A\)、\(B\) 两点,过 \(A\) 作 \(AD\perp l\), 交 \(l\) 于 \(D\), 过 B 作 \(BC\perp l\), 交 \(l\) 于 \(C\), 则 \(A\)、\(O\)、\(C\) 三点共线,\(B\)、\(O\)、\(D\) 三点共线.
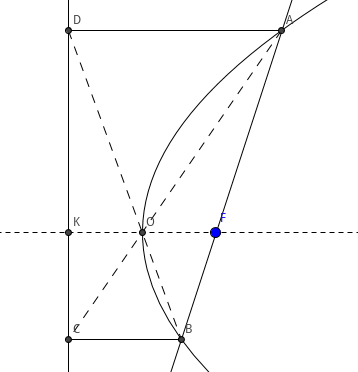
证明
连接 \(AC\) 交轴于 \(O'\)
由 \(\triangle{AO'F}\sim \triangle{ACB}\) 得
\( \frac{BC}{O'F}= \frac{AB}{AF} \)
\( \frac{BF}{O'F}= \frac{AF+BF}{AF} \)
\( \frac{BF}{O'F}= 1+\frac{BF}{AF} \)
\( \frac{1}{O'F}= \frac{1}{BF}+\frac{1}{AF} \)
由结论 2 推论 1 得
\( \frac{1}{O'F}= \frac{2}{p} \)
\( O'F= \frac{p}{2} \)
\( \therefore \) \(O'\) 与 \(O\) 重合
\( \therefore \) \(A\)、\(O\)、\(C\) 三点共线
同理可得 \(B\)、\(O\)、\(D\) 三点共线.
\( \therefore \) 结论成立.
下面用坐标法证明抛物线切线的一个几何性质,作为描述抛物线切线的几何条件。
定理 在平面直角坐标系 \(xOy\) 中,焦点为 \( (0, \frac{p}{2}) \), 准线为 \( y=-\frac{p}{2} \) 的抛物线的方程为 \( x^2=2py \).
证明略.
结论 6 设抛物线顶点为 \(O\), 过顶点的切线为 \(l\), 抛物线上有一异于顶点的点 \(P\). 过点 P 作抛物线的切线 \(m\), 交 \(l\) 于 \(M\), \(P\) 在 \(l\) 上的投影为 \(P'\), 则 \(M\) 是 \(OP\) 的中点.
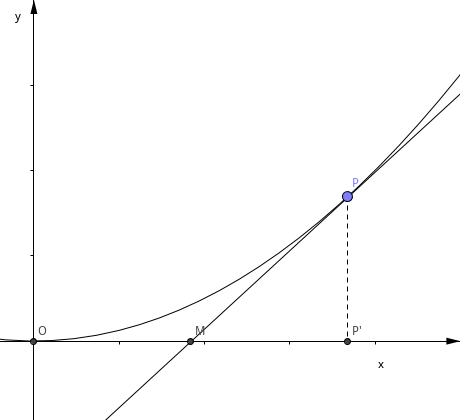
证明
如图建系. 设 \( P(x_0, y_0) \)
\( y=\frac{x^2}{2p} \)
\(\Rightarrow y'=\frac{x}{p} \)
\(\Rightarrow m: y-y_0 = \frac{x_0}{p}(x-x_0)\)
令 \( y=0 \), 得
\( -y_0 = \frac{x_0}{p}(x-x_0)\)
解得
\( x = \frac{x_0}{2} \)
\( \therefore \) 结论得证
结论 7 设抛物线顶点为 \(O\), 焦点为 \(F\), 准线为 \(l\), 轴与准线的交点为 \(K\), 过顶点的切线为 \(m\), 抛物线上有一异于顶点的点 \(P\). 过点 \(P\) 作抛物线的切线 \(t\), 交 \(m\) 于 \(M\). 过 \(P\) 作 \(PD\perp l\), 交 \(l\) 于 \(D\), 则 \(F\)、\(D\)、\(M\) 三点共线,切线 \(PM\) 是 \(FD\) 的垂直平分线.

证明
由 \(O\) 是 \(KF\) 的中点及结论 6 可知,\(F\)、\(D\)、\(M\) 三点共线
\( \therefore \) \( DM=FM \)
又 \( \because \) \( PF=PD \), \( MP=MP \)
\( \therefore \) \( \triangle{PMF}\cong \triangle{PMD} \)
\( \therefore \) \(PM\) 垂直平分 \(FD\)
\( \therefore \) 结论得证
推论 从抛物线的焦点射出的光线,经抛物线反射后沿与抛物线的轴平行的方向射出.
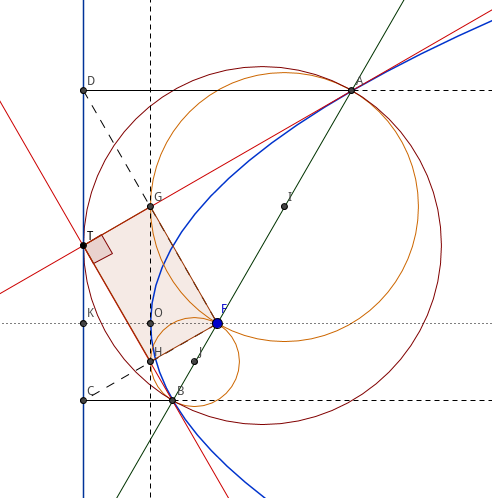
结论 8 设抛物线焦点为 \(F\), 准线为 \(l\), 过顶点的切线为 \(m\), 过 \(F\) 的直线与抛物线交于 \(A\)、\(B\) 两点,过 \(A\) 作 \(AD\perp l\), 交 \(l\) 于 \(D\), 过 B 作 \(BC\perp l\), 交 \(l\) 于 \(C\), 过 \(A\)、\(B\) 作分别抛物线的切线 \(t_1\)、\(t_2\), \( t_1\cap m=G \), \( t_2\cap m=H \), 则 \(t_1\) 与 \(t_2\) 的交点 \(T\) 在 \(l\) 上,\(TC=TD\), 且 \(TA\perp TB\).
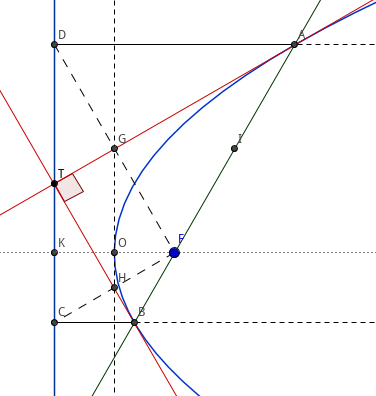
证明
设 \( t_1\cap l=T_1 \), \( t_2\cap l=T_2 \).
由结论 4 及 结论 7 知,\(T_1G\perp FD\), \(CF\perp FD\)
\( \therefore \) \(T_1G\parallel CF\)
又由结论 7 知,\(G\) 是 \(FD\) 的中点
\( \therefore \) \(T_1G\) 是 \(\triangle{DFC}\) 的中位线
\( \therefore \) \(T_1\) 是 \(CD\) 的中点
同理可知,\(T_2\) 也是 \(CD\) 的中点
\( \therefore \) \(T_1\) 与 \(T_2\) 重合
\( \therefore \) \(t_1\) 与 \(t_2\) 在 \(m\) 上交于一点
设这一点为 \(T\).
由结论 4 及 结论 7 知,\(\angle{TGF}=\angle{GFH}=\angle{FHT}=90^{\circ}\)
\( \therefore \) \(\angle{HTG}=90^{\circ}\)
\( \therefore \) \(TG\perp TH\), 即 \(TA\perp TB\)
综上,结论得证.
推论 1 四边形 \(TGFH\) 是矩形.
推论 2 以 \(AB\) 为直径的圆与准线相切,以 \(AF\) 为直径的圆、以 \(BF\) 为直径的圆与 \(m\) 相切.
能想到的性质暂时就这么多。欢迎补充。



