版权声明:本系列文章为博主原创文章,转载请注明出处!谢谢!
本章索引:
从第3章的Logistic回归算法开始,我们一直在讨论分类问题。在各种不同的分类算法中,...,我们一直在讨论如何分类,而没有考虑到分类的效果如何。假设不考虑分类算法本身的思想,运算复杂度等问题,是不是所有的分类效果都是一样的呢?答案是否定的。本章将带领大家一起讨论这个问题,以及由此引出的一类非常重要的分类算法 -- 支持向量机。在录制CS229的时候,吴老师不断强调支持向量机在分类算法问题中的重要性,并认为它在各方面的表现都不比神经网络逊色。不过目前在在人工智能领域貌似是神经网络用的更多一些,不太确定是不是因为这些年神经网络的发展更好,毕竟CS229已经录完10多年了。在求解支持向量机问题的时候,可以使用核函数来提到计算的效率。本章将设计大量的最优化问题,如果最优化的基本问题遗忘的话,建议回去再看一遍番外篇。
1. 最优分类问题的讨论
2. 最优间隔分类器
3. 支持向量机算法
4. 核函数
5. 正规化技术和不可分场景
6. SMO算法
1. 最优分类问题的讨论
在二分类算法中,我们最终的目的是找到一个超平面来划分两类数据。例如,待分类的样本分布在二维空间,那么超平面就是一条直线;如果是三维空间,那么超平面就是一个平面;一般情况下,对于任意维的空间,我们把这个界限称为超平面。直觉上,越靠近这个超平面的样本点,我们认为它和另一类的距离越近,分类的确定性就越低;越远离超平面的样本点,它的分类确定性就越高。比如下面的图:虽然A和C都属于"X"类,但我们认为A属于"X"类的确定性要大于C属于"X"类的确定性。
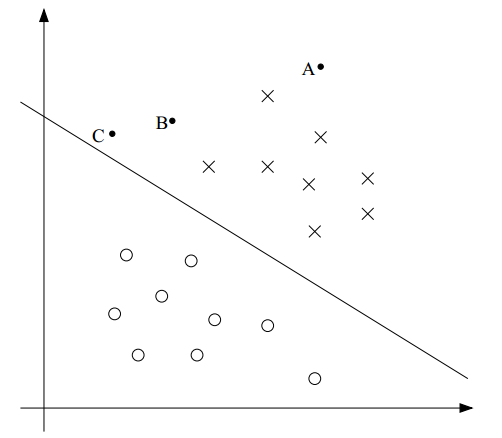
另一方面,如果分界超平面再向右上移动一些,那么有可能C就被分到"O"类中了。很明显C距离"X"类更近一些,它更应当被分到"X"类。把C分到"O"类的超平面不是一个好的分界超平面。正如本章索引中提到的,我们的确需要关注分类算法的效果,使得分界超平面的位置能更好的区分两类样本。什么叫更好的分类的效果呢?之前也提到了,我们对A属于"X"类非常确信,因为它更远离分界超平面。因此,直觉上,如果一个分界超平面能尽可能的原理样本点,那么它的分类效果就非常的好。
下面让我们用数学语言来描述这一结论。
为了更好的表示支持向量机算法,我们需要对之前用在分类算法中的表达式做一些修改:
(1) 我们用$y\in\{-1,1\}$来表示二分类算法中的标签,代替了以前的$y\in\{0,1\}$。并用$y=1$表示上图中的“X"类,用$y=-1$表示"O"类。
(2) 我们丢弃$x_0=1$的假设和$\theta_0x_0+\theta_1x_1+\theta_2x_2 = \sum_{i=0}^n \theta_ix_i = \theta^Tx$的表示方法,改为$b+\theta_1x_1+\theta_2x_2 = b + \sum_{i=1}^n \theta_ix_i = w^T +b$的形式,其中$w=[\theta_1,\cdots,\theta_n]^T$。也就是说,我们现在把截距单独的拿出来,表示为$b$,并用$w$代替之前的$\theta$。
因此,分类算法的假设$h_\theta(x)$表示为:
\begin{equation} h_{w,b}(x) = g(w^Tx+b) \end{equation}
其中,当$z\geq 0$时$g(z) = 1$;其他情况下 $g(z) = -1$。
下面介绍函数间隔和几何间隔。这两个概念是定量描述分类超平面效果好坏的标准,也不断出现在本章后面的算法中。
对于训练集合中的训练样本$(x^{(i)}, y^{(i)})$,定义$(w,b)$相对于它的函数间隔(Functional Margin)为:
\begin{equation*} \hat{\gamma}^{(i)} = y^{(i)}(w^Tx +b) \end{equation*}
在这个定义下有如下结论:
(1) 如果$y^{(i)}(w^Tx+b) \ge 0$,那就表明我们对这个训练样本的预测是正确的。(对照上面的图,在二维空间思考下,应该能想明白)
(2) 如果$y^{(i)} = 1$,为了使函数间隔更大,我们应当让(w^T+b)是一个较大的正数;反之,如果如果$y^{(i)} = -1$,为了使函数间隔更大,我们应当让(w^T+b)是一个较大的负数。
结论(2)使得我们不好直接用函数间隔来衡量超平面的分类效果。我们上面讲过,对于$g(z)$,当$z\geq 0$时$g(z) = 1$;其他情况下 $g(z) = -1$。只有$z$的正负会影响$g$的取值,因此,我们完全可以任意缩放$(w,b)$而不影响$g$和$h_\theta(x)$的取值,因为$g(w^Tx+b) = g(2w^Tx+2b)$,结果就是我们总可以取到无限大的函数间隔。
这是针对一个训练样本的函数间隔的定义。针对整个训练集合,我们定义函数间隔为;
\begin{equation*} \hat{\gamma} = \mathop{min}\limits_{i=1,\cdots,m}\hat{\gamma}^{(i)} \end{equation*}
对于训练集合中的训练样本$(x^{(i)}, y^{(i)})$,定义$(w,b)$相对于它的几何间隔(Geometric Margin)为:
\begin{equation*}
\gamma^{(i)} = y^{(i)}((\frac{w}{\Vert w \Vert})^T x^{(i)} + \frac{b}{\Vert w \Vert})
\end{equation*}
我们借助下图来解释它的意义:
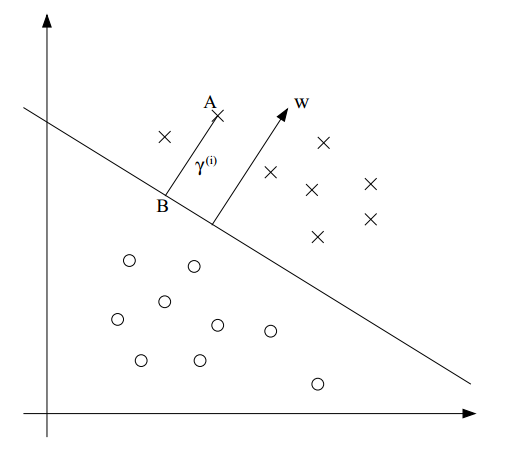
假设我们想计算样本点A $(x^{(i)}, y^{(i)}$到超平面的几何距离$\gamma^{(i)}$,也就是线段AB。图中的分类超平面其实就是$w^Tx+b=0$,这个超平面的法向量是$w$,单位法向量是$w/\Vert w \Vert$。由于点A代表$x^{(i)}$,因此B为: $x^{(i)} - \gamma^{(i)} \cdot w/\Vert w \Vert$。同时,B也在超平面$(w^Tx+b)$上,故带入,有
\begin{equation*}
w^T(x^{(i)} - \gamma^{(i)} \frac{w}{\Vert w \Vert}) + b =0
\end{equation*}
解出$\gamma^{(i)}$,就可得到:
\begin{equation*}
\gamma^{(i)} = (\frac{w}{\Vert w \Vert})^T x^{(i)} + \frac{b}{\Vert w \Vert}
\end{equation*}
上面只是考虑了$y=1$的情况,如果推广到一般情况,那么就得到了上面几何间隔的定义:
\begin{equation*}
\gamma^{(i)} = y^{(i)}((\frac{w}{\Vert w \Vert})^T x^{(i)} + \frac{b}{\Vert w \Vert})
\end{equation*}
从几何间隔的定义可以得到几何间隔的重要性质:我们可以任意缩放$w$和$b$,而不改变几何间隔。
观察下函数间隔和几何间隔之间的关系,很明显,如果$\Vert w \Vert = 1$,那么几何间隔就等于函数间隔。
最后,把几何间隔的定义推广到整个训练集合的几何间隔,类似于有函数间隔,我们有:
\begin{equation*} \gamma = \mathop{min}\limits_{i=1,\cdots,m} \gamma^{(i)} \end{equation*}
总结:上面的讨论告诉我们,分类算法不仅要保证分类的正确性,还要进一步保证对于分类结果的确定程度。我们定义了函数间隔和几何间隔来定量描述分类的确定程度。
2. 最优间隔分类器
在上节的讨论中了解到,为了得到最好的分类效果,我们应当寻找一个几何间隔尽可能大的判决边界。用最优化的思想来描述这种需求。
假设训练集合是线性可分的,那么上面的需求等价于下面的最优化问题:
\begin{equation*}
max_{\gamma,w,b}\ \ \gamma
\end{equation*}
\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq \gamma, \ i=1,\cdots,m
\end{equation*}
\begin{equation*}
\Vert w \Vert =1
\end{equation*}
目标函数的目的是最大化$\gamma$,使得训练集合中所有训练样本的函数间隔都大于$\gamma$,且$\Vert w \Vert =1$。约束$\Vert w \Vert =1$的目的是使得函数间隔等于集合间隔。如果能求解这个最优化问题,那么最优间隔分类器的就得到了。
事与愿违,问题中的等式约束条件$\Vert w \Vert =1$是一个非常讨厌的非凸约束,我们无法对问题进行有效的求解。因此,我们改写上述问题:
\begin{equation*}
max_{\gamma,w,b}\ \ \frac{\hat{\gamma}}{\Vert w \Vert}
\end{equation*}
\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq \hat{\gamma}, \ i=1,\cdots,m
\end{equation*}
这里,我们改为优化$\frac{\hat{\gamma}}{\Vert w \Vert}$。这个问题和上一个问题是等价的,只是摆脱了$\Vert w \Vert =1$这个非凸约束。然而,目标函数$max_{\gamma,w,b}\ \ \frac{\hat{\gamma}}{\Vert w \Vert}$仍然是一个非凸函数,因此这也不是一个凸优化问题(可曾记得,凸优化问题要求目标函数和约束条件都是凸函数?)。
既然还是不行,那我们再进一步。记得之前的结论吧,我们可以任意缩进$w$和$b$,这并不会改变几何间隔的大小。那就开干,在上面优化问题的基础上,我们缩进$w$和$b$,直到函数间隔$\hat{\gamma}=1$。现在好了,本来待优化的目标函数是$\frac{\hat{\gamma}}{\Vert w \Vert}$,现在分子被我们缩进成了1,我们优化的目标就变成了最大化$\frac{1}{\Vert w \Vert}$。等价的,我们可以转化为下列优化问题:
\begin{equation*}
min_{\gamma,w,b}\ \ \frac{1}{2}{\Vert w \Vert}^2
\end{equation*}
\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq 1, \ i=1,\cdots,m
\end{equation*}
这下,目标函数和约束条件都是凸函数了,可以用很多软件直接进行无定制化的求解。
3.支持向量机算法
到这里,最优间隔分类器的问题应该是已经结束了,我们还要继续做什么呢?我们能做的,就是继续为算法寻找更高效的求解方法。继续前进需要了解拉格朗日乘数法,这是一种凸优化问题的求解方法,我把它贴在这里。请确保你完全看明白了再继续。
回到我们的上节最后的优化问题:
\begin{equation*}
min_{\gamma,w,b}\ \ \frac{1}{2}{\Vert w \Vert}^2
\end{equation*}
\begin{equation*}
s.t.\ \ y^{(i)}(w^T x^{(i)} + b) \geq 1, \ i=1,\cdots,m
\end{equation*}
把约束条件写成函数$g_i(w)$,即
\begin{equation*} g_i(w) = -y^{(i)}(w^T x^{(i)} +b) +1 \leq 0 \end{equation*}
根据KKT对偶补充条件,只有使得$g_i(w)=0$的样本点,才能有$\alpha_i \ge 0$。$g_i(w)=0$意味着函数间隔$-y^{(i)}(w^T x^{(i)} +b)$取到了最小值1,如下图虚线上的三个点(两个"X"和一个"O")。只有这三个训练样本对应的的$\alpha_i$是非0的。这三个点就称为支持向量。一般来讲,支持向量的数量是很少的。
正如我们在介绍拉格朗日乘数法的对偶形式时用的内积一样,现在让我们把我们的算法也写成内积的形式,这对我们后面的核函数来说是很重要的一步。
构建拉格朗日算子如下:
\begin{equation*}
\mathcal{L} (w,b,\alpha) = \frac{1}{2} {\Vert w \Vert}^2 - \sum_{i=1}^m \alpha[y^{(i)}(w^T x^{(i)} + b) - 1]
\end{equation*}
让我们来找到上述问题的对偶形式。为了得到对偶形式,我们需要先找到合适的$w$和$b$,使得$\mathcal{L} (w,b,\alpha) $最小化,并得到$\theta_D$。
对$w$和$b$求偏导即可,然后让偏导数等于零即可:
\begin{equation*}
\nabla \mathcal{L} (w,b,\alpha) = w - \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)} = 0
\end{equation*}
求解,得到:
\begin{equation*}
w= \sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}
\end{equation*}
我们把w带入拉格朗日乘数,然后化简,得到:
\begin{equation*}
\mathcal{L} (w,b,\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)} - b\sum_{i=1}^m \alpha_i y^{(i)}
\end{equation*}
然后再对$b$求偏导:
\begin{equation*}
\frac{\partial}{\partial b} \mathcal{L} (w,b,\alpha) = \sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}
对比上一个式子,它的最后一项就是0。所以得到以下结果:
\begin{equation*}
\mathcal{L} (w,b,\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j (x^{(i)})^T x^{(j)}
\end{equation*}
然后,我们把$\alpha_i \geq 0$和对$b$的偏导的结果放在一起,就有下面的对偶优化问题:
\begin{equation*}
max_\alpha \ \ W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2}\sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle
\end{equation*}
\begin{equation*}
s.t.\ \ \alpha_i \geq 0, \ i=1,\cdots,m
\end{equation*}
\begin{equation*}
\sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}
我们可以解决这个对偶问题,就等于解决了原问题。在上面这个优化问题中,待优化的参数是$\alpha$,如果我们可以直接求出$\alpha$,那么我们可以用公式9去找到最优的$w$(作为$\alpha$的函数),然后再用原问题最优的b:
\begin{eqnarray*}
w^T x +b & = & (\sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}) ^T x + b \\
& = & \sum_{i=1}^m \alpha_i y^{(i)} \langle x^{(i)} ,x \rangle + b
\end{eqnarray*}
观察一下公式(9),我们发现,$w$的值之和$\alpha$有关。如果已经根据训练集合建立了模型,那么当我们有新的样本$x$需要预测时,我们要计算$w^T x +b $,然后如果结果大于0,就断定$y=1$:
\begin{eqnarray*}
w^T x +b & = & (\sum_{i=1}^m \alpha_i y^{(i)} x^{(i)}) ^T x + b \\
& = & \sum_{i=1}^m \alpha_i y^{(i)} \langle x^{(i)} ,x \rangle + b
\end{eqnarray*}
因此,如果我们能得到$\alpha$,那么我们只需要计算$x$和训练集合中的其他样本的内积即可。另外,之前也提到了,除了少量的支持向量,其他的$\alpha$都是0,因此,我们只需要计算$x$和支持向量之间的内积。
总结:我们深入研究原问题的对偶问题,得到了很多有用的结论。最重要的是,我们最终把问题转化成了特征向量之间的内积形式。这就是支持向量机算法。在下一部分,我们介绍核函数,它可以帮助我们高效的解决支持向量机算法,并且可以求解高维甚至无限维问题。
4. 核函数
回想我们在线性回归课程中的一个例子,我们用住房面积$x$估计房屋价格的时候,曾经用二次曲线$y=\theta_0+\theta_1x+\theta_2x^2$来做拟合。本来只有一个输入变量$x$的问题转化成了多个,这里是两个。某些场景下,我们需要做这种输入特征的映射,比如训练集合用三次方曲线建模时更好,我们就定义这样的映射为$\phi$,$\phi:\ \mathbb{R} \mapsto mathbb{R}^3 $:
\begin{equation*} \phi(x) = \begin{bmatrix} x \\ x^2 \\ x^3 \end{bmatrix} \end{equation*}
在这里,如果我们把回归问题改成分类问题,例如根据房屋面积判断房屋在六个月内是否能卖出去,那么我们可以用支持向量机算法来计算。之前我们讨论的支持向量机算法中,输入变量都是标量$x$,现在都替换成了三维向量$\phi(x)$,之前支持向量机算法中的内积$\langle x,z \rangle$也要替换成$\langle \phi(x), \phi(z) \rangle$。一般来讲,给定一个映射$\phi$,我们定义相应的核函数为$K(x,z) = \phi(x)^T \phi(x)$。因此,所有内积$\langle x,z \rangle$都可以替换成核函数$K(x,z)$。
此时,给定$\phi$,我们可以很容易的得到$\phi(x)$和$\phi(z)$,然后求内积从而计算出$K(x,z)$。神奇的是,有时候计算$K(x,z)$是很容易的,反而计算$\phi(x)$是很难的,比如映射的维数很高的时候。在这种情况下,我们可以用核函数$K(x,z)$很容易的计算出高维空间的支持向量机,而不用去计算映射$\phi(x)$。
来看一个具体的例子,假设$x, z \in \mathbb{R}^n$,核函数为$K(x,z)$ =(x^Tz)^2,即
\begin{eqnarray*}
K(x,z) & = & (\sum_{i=1}^n x_i z_i)(\sum_{j=1}^n x_j z_j) \\
& = & (\sum_{i=1}^n \sum_{j=1}^n x_i x_j z_i z_j \\
& = & (\sum_{i,j=1}^n (x_i x_j) (z_i z_j) \\
& = & \langle (\phi(x))^T,(\phi(x)) \rangle
\end{eqnarray*}
因此,$K(x,z)=\phi(x)^T \phi(z)$,其中,$n=3$时的映射$\phi$是:
\begin{equation*} \phi(x) = \begin{bmatrix} x_1 x_1 \\ x_1 x_2 \\ x_1 x_3 \\ x_2 x_1 \\ x_2 x_2 \\ x_2 x_3 \\ x_3 x_1 \\ x_3 x_2 \\ x_3 x_3 \end{bmatrix} \end{equation*}
我们注意到,计算高维的$\phi(x)$需要$O(n^2)$的时间复杂度,但是计算$K(x,z)$只需要$O(n)$的时间复杂度。
再来看另一个相关的核函数:
\begin{eqnarray*}
K(x,z) & = & (x^T z + c)^2 \\
& = & \sum_{i,j=1}^n(x_i x_j) (z_i z_j) + \sum_{i=1}^n (\sqrt{2c}x_i) (\sqrt{2c} z_i) + c^2
\end{eqnarray*}
$n=3$时的映射是:
\begin{equation*} \phi(x) = \begin{bmatrix} x_1 x_1 \\ x_1 x_2 \\ x_1 x_3 \\ x_2 x_1 \\ x_2 x_2 \\ x_2 x_3 \\ x_3 x_1 \\ x_3 x_2 \\ x_3 x_3 \\ \sqrt{2c}x_1 \\ \sqrt{2c}x_2 \\ \sqrt{2c}x_3 \\ c \end{bmatrix} \end{equation*}
这样可以用参数$c$控制着$x_i$和$x_i x_j$之间的相对权重。
一般来讲,核函数$K(x,z) = (x^T z + c)^d对应着$ \begin{pmatrix} n+d \\ d \end{pmatrix}$维的映射,计算它的时间复杂度是$O(n^d)$,而计算核函数$K(x,z)$的时间复杂度却仍然是$O(n)$,且完全不涉及高维向量的计算。
下面来讨论核函数的选择相关的直觉(不一定完全正确)。如果$\phi(x)$和$\phi(z)$是足够相近的,那么$K(x,z)=\phi(x)^T \phi(z)$的值应该很大。反之,如果$\phi(x)$和$\phi(z)$不相近,类似于正交关系,那么$K(x,z)=\phi(x)^T \phi(z)$应该接近于0。所以,我们可以认为$K(x,z)$是$\phi(x)$和$\phi(z)$相似程度的大致估计。
我们可以根据上述直觉提出一些靠谱的核函数:
\begin{equation*} K(x,z)=exp(\ \frac{{\Vert x-z \Vert}^2}{2\sigma^2}) \end{equation*}
很容易看出来,如果$x$和$z$比较接近的话,它的值为1;反之,则值为0。这个核函数叫高斯核函数,它对应的映射$\phi$是无限维的。
如何判断是一个核函数是合法的呢?
假设$K$的确是一个合法的核函数,它对应的映射是$\phi$。对于训练集合$\{ x^{(1)},\cdots, x^{(m)} \}$,定义一个$m \times m$的矩阵K,它的第$(i,j)$个元素的值$K_{i,j} = K(x^{(i)}, x^{(j)} )$。这个矩阵K称为核矩阵(表示方法有点混乱,都是用K表示,但一个是函数,一个是矩阵)。
根据假设,$K$是一个合法核函数,那么必有 $K_{ij} = K(x^{(i)}, x^{(j)}) = \phi(x^{(i)})^T \phi(x^{(j)}) = \phi(x^{(j)})^T \phi(x^{(i)}) = K(x^{(j)}, x^{(i)}) = K_{ji}$,即$K$是一个对称矩阵。
用$\phi_k(x)$表示向量$\phi(x)$的第$k$个坐标,对于任意向量$z$,都有:
\begin{eqnarray*}
z^T K z & = & \sum_i \sum_j z_i K_{ij} z_j \\
& = & \sum_i \sum_j z_i \phi(x^{(i)})^T \phi(x^{(j)}) z_j \\
& = & \sum_i \sum_j z_i \sum_k \phi_k(x^{(i)}) \phi_k(x^{(j)}) z_j \\
& = & \sum_k \sum_i \sum_j z_i \phi_k(x^{(i)}) \phi_k(x^{(j)}) z_j \\
& = & \sum_k (\sum_i z_i \phi_k(x^{(i)}))^2 \\
\geq 0
\end{eqnarray*}
也就是说,对于任意的$z$,都有$K \geq 0$。总结成以下结论:
Mercer定理:给定$K: \mathbb{R}^n \times \mathbb{R}^n \mapsto \mathbb{R}$. K是合法核函数的充要条件是对于任意的$\{ x^{(1)},\cdots, x^{(m)} \}, (m \le \infty)$,对应的核矩阵是对称半正定的。
5. 正则化和线性不可分
直到现在,在我们的假设中,训练集合都是线性可分的。支持向量机算法可以把特征映射到高维,将一些线性不可分的问题转换为线性可分的问题,但我们很难保证总是这样。此外,某些情况下,我们也不希望找出精确的分界平面,例如,下图中的左图展示了一个最优间隔分类器;但当训练集合中混入了一些离群点时,我们找到的最优间隔分类器其实很糟糕,它与样本点之间的间隔很小。
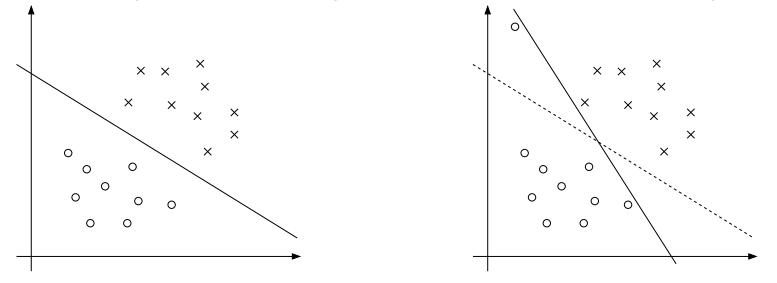
为了解决这类线性不可分问题,我们重构了算法:
\begin{equation*}
min_{\gamma,w,b} \ \ \frac{1}{2} {\Vert w \Vert}^2 + C \sum_{i=1}^m \xi_i
\end{equation*}
\begin{equation*}
s.t. \ \ y^{(i)}(w^T x^{(i)} + b ) \geq 1-\xi_i, \ i=1,\cdots,m
\end{equation*}
\begin{equation*}
\xi_i \geq 0,\ i=1,\cdots,m
\end{equation*}
在函数间隔相关的约束条件上增加了一个惩罚量$\xi_i$ ($L1$正则化),使得函数间隔有可能小于1了(回想,原版的支持向量机算法中,函数间隔最小只能等于1)。并且,如果惩罚项$\xi_i \ge 1$,函数间隔可能是负数。我们之前提过,如果函数间隔$y^{(i)}(w^T x^{(i)} + b ) \ge 0$则表示分类正确。可能出现小于0的函数间隔也就意味着,我们允许分类错误的样本点出现,这可以很好的应对上图中的情形。
这是一个凸优化问题,我们用之前讲过的对偶问题的方式来求解。写出拉格朗日算子:
\begin{equation*}
\mathcal{L} (w,b,\xi,\alpha,\gamma) = \frac{1}{2}w^Tw + C\sum_{i=1}^m \xi_i - \sum_{i=1}^m \alpha_i [y^{(i)} (x^Tw+b)-1 + \xi_i] - \sum_{i=1}^m r_i \xi_i
\end{equation*}
推导出它的对偶形式:
\begin{equation*}
max_\alpha W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle
\end{equation*}
\begin{equation*}
s.t. \ \ 0 \leq \alpha_i \leq C, \ i=1,\cdots,m
\end{equation*}
\begin{equation*}
\sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}
注意到,在做了$L1$正则化以后,对偶问题唯一的改变就是约束条件从$0 \leq \alpha$变成了 $0 \leq \alpha \leq C$。KKT对偶补充条件是:
\begin{equation*}
\alpha_i = 0 \Rightarrow y^{(i)} (w^T x^{(i)} + b) \geq 1
\end{equation*}
\begin{equation*}
\alpha_i = C \Rightarrow y^{(i)} (w^T x^{(i)} + b) \leq 1
\end{equation*}
\begin{equation*}
0 \le \alpha_i \le C \Rightarrow y^{(i)} (w^T x^{(i)} + b) = 1
\end{equation*}
6. 顺序最小优化算法
先介绍坐标上升法:
假设我们要优化一个无约束问题:
\begin{equation*}
\max_\alpha W(\alpha_i, \alpha_2, \cdots, \alpha_m)
\end{equation*}
方法是描述如下:
Loop until convergence: {
For $i=1,\cdots,m,${
$alpha_i := argmax_{\hat{alpha}_i}\ W(\alpha_i,\cdots,\alpha_{i-1}, \hat{\alpha}_i, \alpha_{i+1},\cdots, \alpha_m)$
}
}
解释:每次迭代,坐标上升法保持所有$\alpha$固定,除了$\alpha_i$。然后相对于这个参数使函数取最大值。结合下面的图再直观的理解一下:

假设只有两个$\alpha$,用横坐标表示$\alpha_1$,纵坐标表示$\alpha_2$,因为每次迭代都是只改变一个$\alpha$,故优化的轨迹方向都是与坐标轴平行的。
回到上节的优化问题,让我们来用坐标上升法计算:
\begin{equation*}
max_\alpha W(\alpha) = \sum_{i=1}^m \alpha_i - \frac{1}{2} \sum_{i,j=1}^m y^{(i)} y^{(j)} \alpha_i \alpha_j \langle x^{(i)}, x^{(j)} \rangle
\end{equation*}
\begin{equation*}
s.t. \ \ 0 \leq \alpha_i \leq C, \ i=1,\cdots,m
\end{equation*}
\begin{equation*}
\sum_{i=1}^m \alpha_i y^{(i)} = 0
\end{equation*}
注意约束 $\sum_{i=1}^m \alpha_i y^{(i)} = 0$,如果我们直接应用坐标上升法,固定所有的$\alpha$除了$\alpha_i$,只改变$\alpha_i$,那么... 我岂不是连$\alpha_i$都不能改变了?怎么优化啊?所以,要对初始的算法做一些调整,每次改变两个$\alpha$值。这个算法就称为序列最小优化算法(Sequential Minimal Optimizaiton, SMO),最小的意思是我们希望每次该表最小数目的$\alpha$。这个算法的效率非常高,与牛顿法比较的话,它收敛所需的迭代次数会比较多,但每次迭代的计算代价通常比较小。
Repeat till convergence {
1. Select some pair $\alpha_i$ and $\alpha_j$ to update next (using a heuristic that tries to pick the two that will allow us to make the biggest progress towards the global maximum).
2. Reoptimize $W(\alpha)$ with respect to $\alpha_i$ and $\alpha_j$, while holding all the other $\alpha_k’s (k \neq i, j) fixed.
}
我们只要一直运行算法,直到满足上一节的收敛条件即可。问题是,算法的第2步要求优化$W$,我们应该怎样做呢?下面以$\alpha_1$和$\alpha2$为例来讲解这个过程。
根据约束条件,有
\begin{equation*} \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = -\sum{i=3}^m \alpha_i y^{(i)} \end{equation*}
由于等式右边是固定的,我们就简单的把它记为一个常数$\zeta$,即
\begin{equation*}\alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta \end{equation*}
这是一个约束。还一个约束是
\begin{equation*}
0 \le \alpha_i \le C
\end{equation*}
把可选区域画成图,如下:
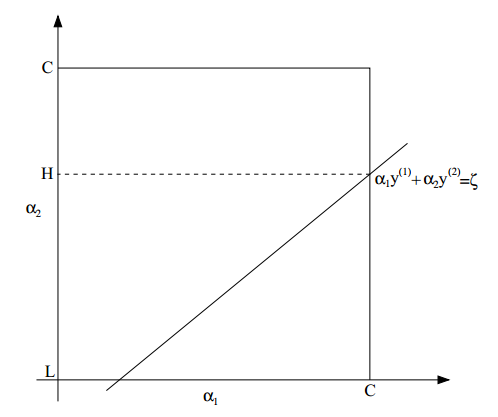
从图中可以看出,$\alpha_2$的取值范围是$[L, H]$,否则,$(\alpha_1, alpha_2)不可能同时满足上面两个约束$。
根据公式$ \alpha_1 y^{(1)} + \alpha_2 y^{(2)} = \zeta $,我们可以把$\alpha_1$写成$\alpha_2$的函数:
\begin{equation*} \alpha_1 = ( \zeta - \alpha_2 y^{(2)}) y^{(1)}. \end{equation*}
然后,有$W(\alpha_1, \alpha_2, \cdots, \alpha_m) = W((\zeta - \alpha_2 y^{(2)}) y^{(1)}, \alpha_2, \cdots, \alpha_m) $。把$\alpha_3,\cdots, \alpha_m$看做常数,可以看出这只是$\alpha_2$的二次函数。如果没有取值范围$[L, H]$的限制的话,只要求导数然后让它为0即可,定义得到的值为$\alpha_2^{new, unclipped}$。再结合取值范围$[L, H]$的限制,最终的优化结果为:
$$ \alpha_2^{new}=\left\{
\begin{array}{rcl}
H & & {\alpha_2^{new, unclipped} \ge H}\\
\alpha_2^{new, unclipped} & & {L \leq \alpha_2^{new, unclipped} \leq H} \\
L & & {\alpha_2^{new, unclipped} \le L}
\end{array} \right. $$



