版权声明:本系列文章为博主原创文章,转载请注明出处!谢谢!
本章索引:
本章将讨论监督学习中的第二个问题 - 分类问题。分类问题和回归问题相似,唯一不同的是分类问题中输出变量$y$的取值是离散值,本章只讨论其中的二值分类问题,即$y$只能取2个离散值:0或者1。例如,如果我们建立一个垃圾邮件分类器,$x^{(i)}$就是邮件的各种特征,$y$如果为1就意味着这是一封垃圾邮件,为0则意味着不是。0一般被称为否定类型,1被称为肯定类型。在分类问题中,给定了$x^{(i)}$,对应的$y^{(i)}也称为训练集合的标签(label).
1. Logistic回归
2. 牛顿法
1. Logistic回归:
第一个要尝试的方法,就是把分类问题看做特殊的回归问题,用之前的回归算法来预测$y$。如前所提,在分类问题中,$y$的取值只能是0或者1,那么得到大于1或者小于0的预测值$h_\theta(x)$将毫无意义。因此,我们不直接使用之前的线性模型$(h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2)$。我们将假设$h_\theta$定义为:
\begin{equation*} h_\theta(x) = g(\theta^Tx) = \frac{1}{1+e^{-\theta^Tx}} \end{equation*}
其中:
\begin{equation*} g(z) = \frac{1}{1+e^{-z}} \end{equation*}
$g(z)$称作Logistic函数或者sigmoid函数。下图是这个函数的曲线:
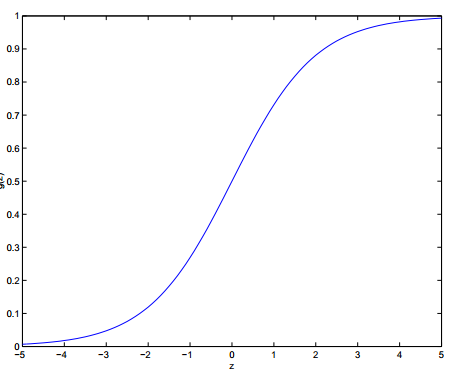
很容易发现,函数$g(z)$的值域在[0,1]上,因此选择这个函数作为$h_\theta(x)$是很自然的。这个函数的导数有一个很有用的性质:
\begin{eqnarray*} g'(z) & = & \frac{d}{dz}\ \frac{1}{1+e^{-z}} \\
& = & \frac{1}{(1+e^{-z})^2} (e^{-z}) \\
& = & \frac{1}{(1+e^{-z})}\cdot (1- \frac{1}{(1+e^{-z})} ) \\
& = & g(z)(1-g(z))
\end{eqnarray*}
问题同样编程如何来拟合$\theta$?在第1张第6节,我们介绍了如何用最大似然估计来进行最小均方回归,这里使用同样的方法。
首先明确分类模型中的一系列的假设。之前的例子中,我们把$y|x;\theta$假设成了高斯分布(随机噪声,中心极限定律),这里因为是二值的分类问题,因此我们假设$y|x;\theta$服从伯努利分布。(这里有一篇博客介绍概率论中的各种模型):
\begin{equation*} P(y=1|x;\theta) = h_\theta(x) \end{equation*}\begin{equation*} P(y=0|x;\theta) = 1 - h_\theta(x) \end{equation*}
我们可以用更紧凑的方式来写上述两个等式:
\begin{equation*} p(y|x;\theta) = (h_\theta(x))^y(1-h_\theta(x))^{1-y} \end{equation*}
假设m个训练样本是独立生成的,我们可以写出参数的似然:
\begin{eqnarray*}L(\theta) & = & p(\vec y| X; \theta) \\
& = & \prod_{i=1}^m p(y^{(i)} | x{(i)};\theta) \\
& = & \prod_{i=1}^m(h_\theta(x^{(i)})^{y^{(i)}} (1-h_\theta(x^{(i)}))^{1-y^{(i)}}
\end{eqnarray*}
转换成对数似然的最大化问题更容易解决:
\begin{eqnarray*} l(\theta) & = & logL(\theta) \\
& = & \sum_{i=1}^m y^{(i)}logh(x^{(i)}) + (1-y^{(i)})log(1-h(x^{(i)}))
\end{eqnarray*}
如何最大化似然呢?同之前线性回归中的方法类似,我们这里用梯度上升。还是先考虑只有一个训练样本的情况,求偏导数:
\begin{eqnarray*}
\frac{\partial}{\partial \theta_j} l(\theta)
& = & (y \frac{1}{g(\theta^Tx)} - (1-y)\frac{1}{1-g(\theta^Tx)}) \frac{\partial}{\partial \theta_j} g(\theta^T) \\
& = & (y \frac{1}{g(\theta^Tx)} - (1-y)\frac{1}{1-g(\theta^Tx)}) g(\theta^Tx)(1-g(\theta^Tx)) \frac{\partial}{\partial \theta_j}\theta^Tx \\
& = & (y(1-g(\theta^Tx)) - (1-y)g(\theta^Tx))x_j \\
& = & (y - h_\theta(x))x_j
\end{eqnarray*}
得到可以用在随机梯度上升的规则:
\begin{equation*} \theta_j := \theta_j + \alpha(y^{(i)} - h_\theta(x^{(i)}))x_j^{(i)} \end{equation*}
讨论:我们比较这个算法和上一章的最小均方误差算法。它们看起来是很类似的,但是因为在两个算法中,$h_\theta(x^{(i)})$的定义形式是不同的,一个是线性函数,另一个是sigmoid函数。即便如此,它们的更新规则居然是完全一样的,这其中有什么更深层次的原因吗?我们将在下一章--广义线性模型中讨论。
最后一点需要注意的:虽然名字是叫xxx回归,但它的的确确是一个分类算法,因为
2. 牛顿法
本章讨论另外一种可以估计对数似然函数$l(\theta)$最小值的方法--牛顿法。在第1章第4节的标准方程方法中,为了得到某个函数的最小值,通常是显式推导这个函数的导数,然后让它为0。同样,为了找出让一个函数的导数近似等于0的方法,我们还可以用迭代的方法运算,同样可以得到似然的最大值。
将上述需求用数学语言描述:
假设有一个函数$f: \mathbb{R} \mapsto \mathbb{R}$, 我们希望能找到一个$\theta$值,使得$f(\theta)=0$,其中$\theta \in \mathbb{R}$。牛顿法的迭代规则如下:
\begin{equation*} \theta := \theta - \frac{f(\theta)}{f'(\theta)} \end{equation*}
结合下图讲解一下它的原理:
最左边的图中,可以看到使得$f(\theta)=0$的$\theta$值大概是1.3。假设我们随机从$\theta=4.5$的初始值开始推导。牛顿法会在$\theta=4.5$的地方画一条切线,并找到使这条切线为零值时的$\theta$值(其实就是切线与y=0的交点),将这个$\theta$作为下一次迭代的值,如中间的图所示。图中可以看出此时的$\theta$值大约为2.8。再执行一次迭代,可以得到最右边的图,此时$\theta$的值大约为1.8。几次迭代之后,最终可以收敛在$\theta=1.3$。
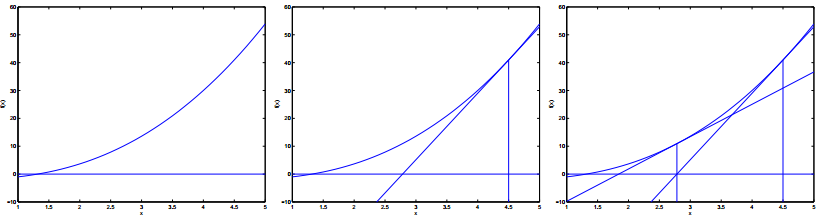
有了这个求解$f(\theta)=0$的方法,我们下面考虑如何把它用在最大似然估计中。前面提到过,使得对数似然函数$l$取到极值的点,就是它的一阶导数$l'(\theta)$为0的点,因此问题就转化成了如何求解$l'(\theta)=0$的问题,因此只要使$f(\theta)=l'(\theta)$即可。那么此时的最大对数似然估计问题的迭代规则可以表示成:
\begin{equation*} \theta := \theta - \frac{l'(\theta)}{l''(\theta)} \end{equation*}
上面只是针对只有一个$\theta$时的情况。一般情况下,$\theta$是一个向量,我们应该如何推广上述算法呢?推广后的更新规则如下(具体是如何推广过来的,本人并没有具体研究,老师也没有讲),该算法也被称为牛顿-拉夫逊方法(Newton-Raphson method):
\begin{equation*} \theta := \theta - H^{-1}\nabla_\theta l(\theta) \end{equation*}
其中,$\nabla_\theta l(\theta)$是标准方程组(第几章)中定义的函数相对于矩阵(向量)的偏导数。$H$是一个$n \times n$的矩阵,称为黑森矩阵(Hessian Matrix),定义如下:
\begin{equation*} H_{ij} = \frac{\partial^2 l(\theta)}{\partial \theta_i \partial \theta_j} \end{equation*}
通常来讲,牛顿法的收敛速度比批梯度下降要快,并且需要的迭代次数也很少,对于几十个甚至上百个特征的训练集合来说,只需要十几次迭代就可以收敛。但是,牛顿法每一次的迭代的代价都很高,因为要计算一个$n \times n$阶矩阵的逆矩阵。尽管如此,在$n$不是很大的时候,它还是很快的。当牛顿法用在Logistic回归中最大化对数似然函数$l(\theta)$时,这种方法也称为Fisher Scoring



