排序总结[3]_线性排序算法
标签(逗号分隔): 线性排序、算法
上一篇介绍了冒泡、直接插入和希尔排序,这一篇介绍几种常见的线性排序算法,需要注意的是这些线性排序算法是非基于比较的排序算法,都有很多使用限制才能达到线性排序的效果。
一、计数排序
基本思想:统计数据的出现次数,然后根据基值排序。
例子:比如统计字符串中字符(ASCII)出现的次数,我们知道ASCII字符只有256个,那么建立一个数组int[] arr=new int[256];然后遍历字符串每个字符(c)对应的位置arr[c]++即可统计出现次数,最后根据arr即可给出排序后的序列。
优势:如果已知数据的值范围,比如统计年龄,身高等问题非常好用。
注意:如果数据是1,0,3,1000000000,...这样的就不值得了
- 平均时间复杂度:O(N)
- 空间复杂度:O(N)
- 稳定性:稳定
- 优化:先求出输入的max和min,然后求出范围这样统计出现次数的数组可以小一点,统计:record[arr[i]-min]++即可。
代码:
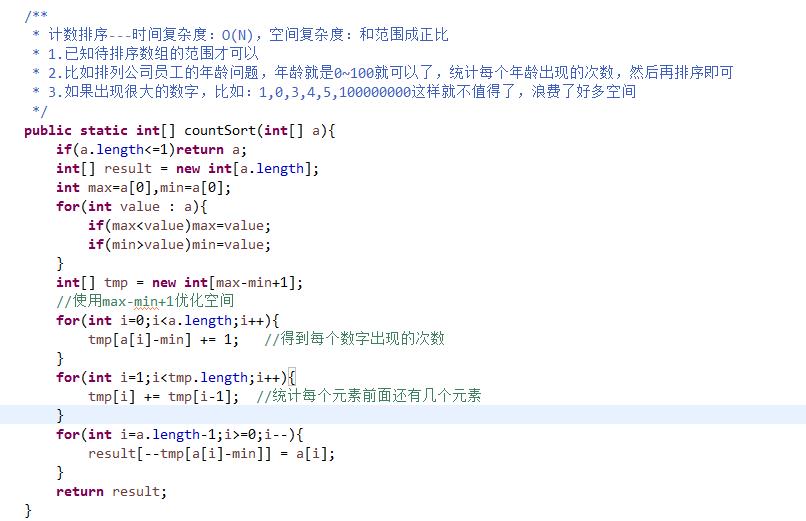
二、基数排序
基本思想:以整形10进制为例,按照每位差分,然后从低位到高位一次排序最后完成就是排序后的序列
基本流程:
第一步:分配,先从各位开始根据位值(0-9)分别放到0-9个桶中(比如53,各位是3,放入3号桶中);
第二步:收集,再将放到0-9号桶中的数据按顺序放到数组中,重复(1)(2)过程,从各位到最高位。
以【521 310 72 373 15 546 385 856 187 147】序列为例,具体细节如下图所示:



平均时间复杂度:O(dn),其中d是整形数据的位数
空间复杂度:O(10n)(10表示0-9,用于存储临时的序列)
稳定性:稳定
代码
/********************************************************
*函数名称:GetNumInPos
*参数说明:num 一个整形数据
* pos 表示要获得的整形的第pos位数据
*说明: 找到num的从低到高的第pos位的数据
*********************************************************/
int GetNumInPos(int num,int pos)
{
int temp = 1;
for (int i = 0; i < pos - 1; i++)
temp *= 10;
return (num / temp) % 10;
}
/********************************************************
*函数名称:RadixSort
*参数说明:pDataArray 无序数组;
* iDataNum为无序数据个数
*说明: 基数排序
*********************************************************/
#define RADIX_10 10 //整形排序
#define KEYNUM_31 10 //关键字个数,这里为整形位数
void RadixSort(int* pDataArray, int iDataNum)
{
int *radixArrays[RADIX_10]; //分别为0~9的序列空间
for (int i = 0; i < 10; i++)
{
radixArrays[i] = (int *)malloc(sizeof(int) * (iDataNum + 1));
radixArrays[i][0] = 0; //index为0处记录这组数据的个数
}
for (int pos = 1; pos <= KEYNUM_31; pos++) //从个位开始到31位
{
for (int i = 0; i < iDataNum; i++) //分配过程
{
int num = GetNumInPos(pDataArray[i], pos);
int index = ++radixArrays[num][0];
radixArrays[num][index] = pDataArray[i];
}
for (int i = 0, j =0; i < RADIX_10; i++) //收集
{
for (int k = 1; k <= radixArrays[i][0]; k++)
pDataArray[j++] = radixArrays[i][k];
radixArrays[i][0] = 0; //复位
}
}
}
三、桶排序
假设输入是一个随机过程产生的[0,1)区间上均匀分布的实数。将区间[0,1)划分成n个大小相等的子区间(桶),每个桶大小1/n:[0,1/n),[1/n,1/2n),[1/2n,1/3n),...将n个元素随机的分配到这些桶中,对桶中的元素进行排序(快排等),然后依次连接桶即可。
对N个数据,M个桶分析:
平均时间复杂度:O(N+C)(假设输入是均匀的才行),C=N*(logN-logM);
最佳时间复杂度:O(N),M=C时候
空间复杂度:O(N+M)
稳定性:稳定
参考代码(百度百科)
public static void basket(int data[])//data为待排序数组
{
int n=data.length;
int bask[][]=new int[10][n];
int index[]=new int[10];
int max=Integer.MIN_VALUE;
for(int i=0;i<n;i++){
max=max>(Integer.toString(data[i]).length())?max:(Integer.toString(data[i]).length());
}
String str;
for(int i=max-1;i>=0;i--){
for(int j=0;j<n;j++){
str="";
if(Integer.toString(data[j]).length()<max){
for(int k=0;k<max-Integer.toString(data[j]).length();k++)
str+="0";
}
str+=Integer.toString(data[j]);
bask[str.charAt(i)-'0'][index[str.charAt(i)-'0']++]=data[j];
}
int pos=0;
for(int j=0;j<10;j++){
for(int k=0;k<index[j];k++){
data[pos++]=bask[j][k];
}
}
for(intx=0;x<10;x++)index[x]=0;
}
}



