排序模拟枚举

1.排序模拟枚举

复杂度

• 一般（最坏）复杂度 ：记号为 O(……)
  均摊复杂度 \(\qquad\quad\,\) ：记号为 Θ(……),但一般写成O(……)
• 约定
  1. 省略系数O(100n)=O(10n)=O(\(\frac{1}{2}\)n)=O(n).
  2. log底数省略

排序

• 选择排序
  这个大家都会，就不详细解释了 （逃

• 插入排序

• 冒泡排序

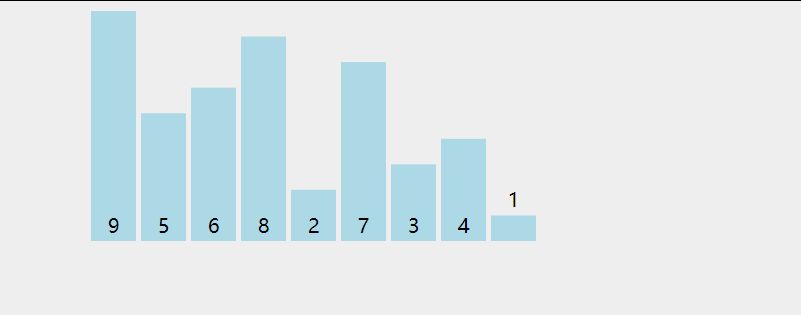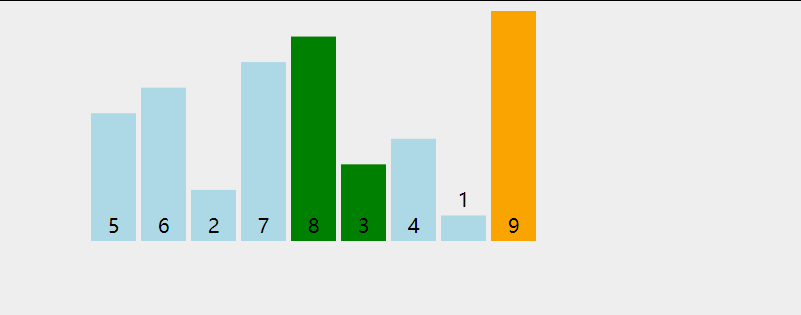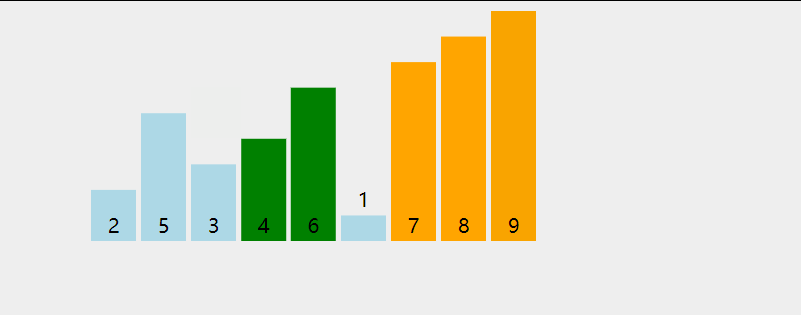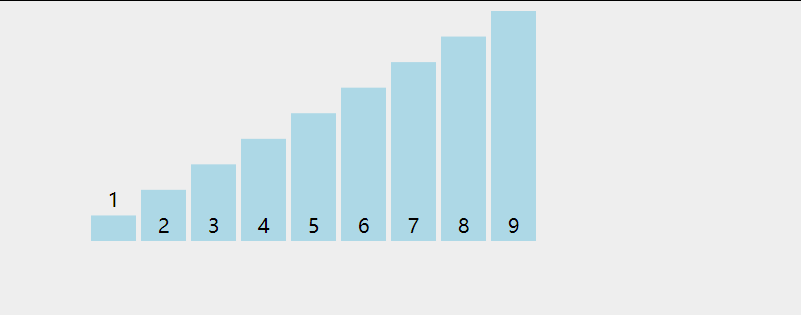
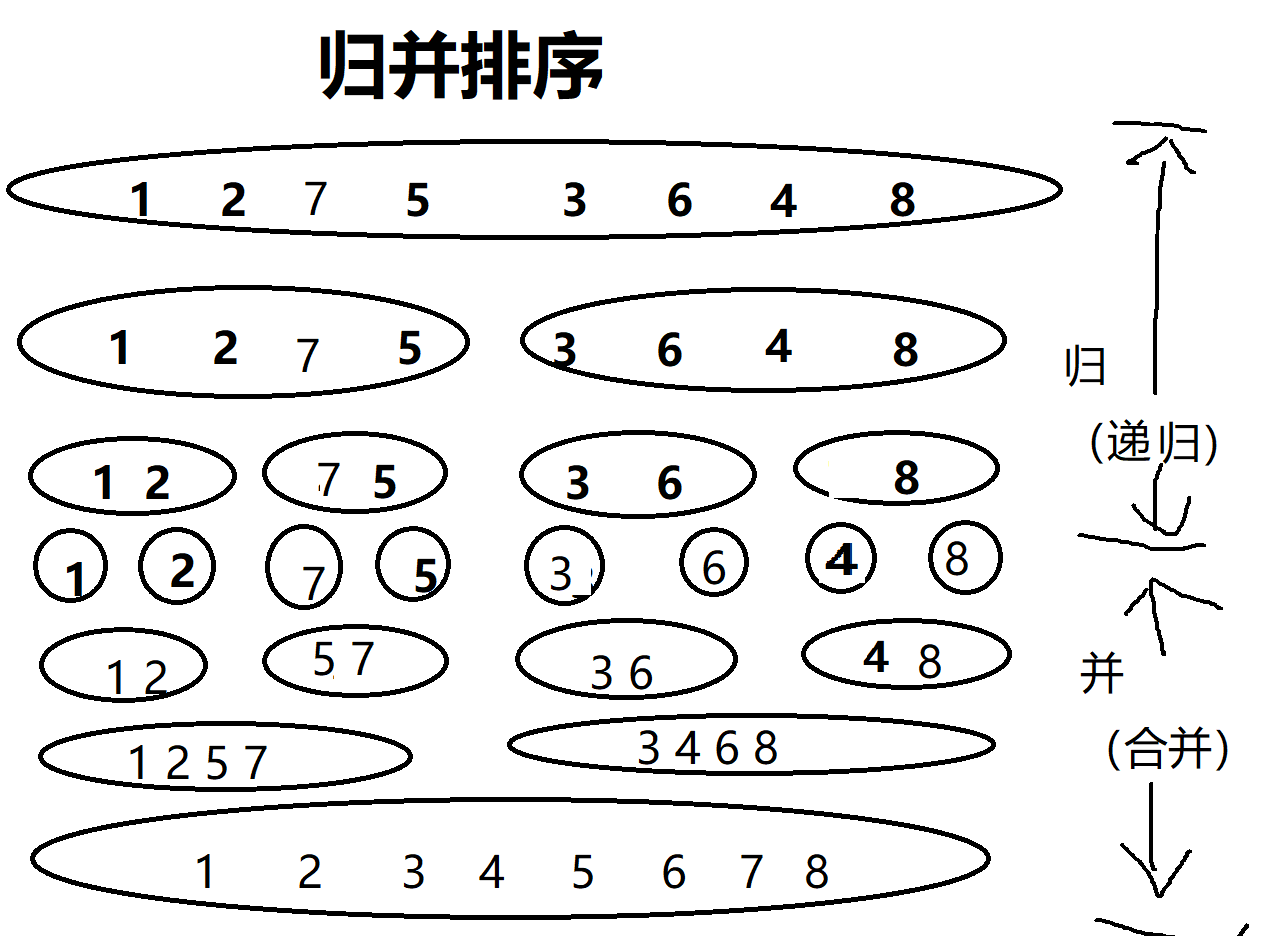
• 归并排序

  详情请见点我

void ms(int b, int e)
{
	if(e-b <= 0) return ;
	int m = (b + e) / 2, p1 = b, p2 = m+1,   i = b;
	ms(b, m); ms(m+1, e);
	while(p1 <= m || p2 <= e)
		if(p2 > e || (p1 <= m && a[p1] <= a [p2]))
			t[i++] = a[p1++];
			else t[i++] = a[p2++];
	for(i = b; i <= e; ++i) a[i] = t[i];
}

• 快速排序

 void Sort(int l, int r)
{
	int i  = l, j = r, x = a[(l + r)/ 2];
	do{
		while(a[i] < x) ++i; while(a[j] > x) --j;
		if(i <= j) swap(a[i++], a[j--]);
	}while(i < j);
	if(i < r) Sort(i, r); if(j > l) Sort(l, j);
}

模拟

模拟，顾名思义，就是题目让你干嘛你就干嘛。

例题 校门外的树

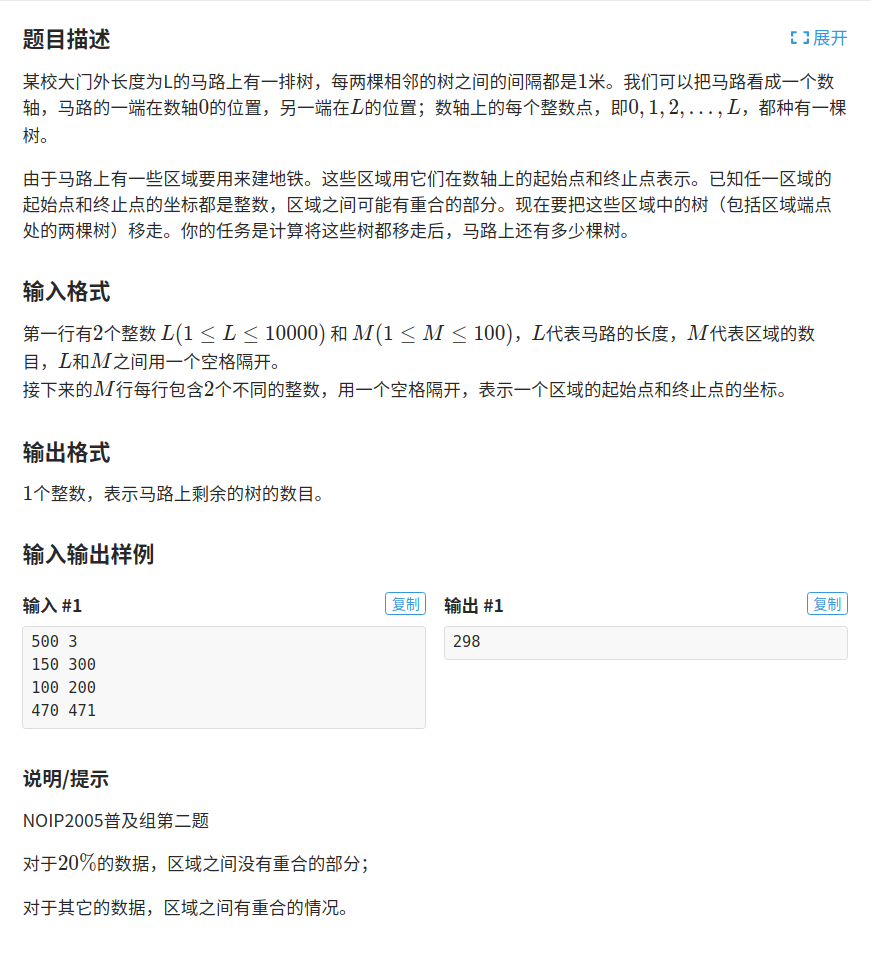
思路：可以建一个数组，保存地铁每一个位置的情况，每次输入l,r，就把这个数组[l,r]部分都变成1，最后再统计有多少0即可

代码如下（勿喷）

#include <iostream>
using namespace std;
const int maxn = 10010;
int tree[maxn];
int main(void)
{
	int l,m,b,e,ans = 0;
	cin>>l>>m;
	for(int i = 0;i < m;i++)
	{
		cin>>b>>e;
		for(int j = b;j <= e;j++)
			tree[j] = 1;
	}
	for(int i = 0;i <= l;i++)
		ans+=!tree[i];
	cout<<ans;
}

枚举

枚举，顾名思义，就是把所有可能的情况都试一遍直到找到正确的答案。

例题 P1219 八皇后

【题目描述】

一个如下的 \(6×6\) 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

上面的布局可以用序列\(2\ 4\ 6\ 1\ 3\ 5\)来描述，第 \(i\) 个数字表示在第 \(i\) 行的相应位置有一个棋子，如下：

行号 \(1\ 2\ 3\ 4\ 5\ 6\)

列号 \(2\ 4\ 6\ 1\ 3\ 5\)

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 \(3\) 个解。最后一行是解的总个数。
【输入格式】
一行一个正整数 \(n\)，表示棋盘是 \(n \times n\) 大小的。
【输出格式】
前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。
输入输出样例

输入 #1 \(\qquad\qquad\qquad\) 输出 #1

6 \(\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 2 4 6 1 3 5
\(\quad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 3 6 2 5 1 4
\(\quad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 4 1 5 2 6 3
\(\quad\qquad\qquad\qquad\qquad\qquad\qquad\quad\) 4

【数据范围】
对于 \(100\%\) 的数据，\(6 \leq n \leq 136\)

USACO Training Section 1.5

代码

#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int tot = 0,n;
int C[10000] = { 0 };
int vis[10000][10000] = { 0 };
vector<vector<int> >ans;
void search(int cur)
{
	if (cur == n)
	{
		tot++;
		vector<int> v;
		for (int i = 0; i < n; ++i)
		{
			v.push_back(C[i]);
		}
		ans.push_back(v);
	}
	else for (int i = 0; i < n; ++i)
	{
		if (!vis[0][i] && !vis[1][cur + i] && !vis[2][cur - i + n])
		{
			C[cur] = i;
			vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 1;
			search(cur + 1);
			vis[0][i] = vis[1][cur + i] = vis[2][cur - i + n] = 0;
		}
	}
}
bool cmp(vector<int>& a, vector<int>& b)
{
	for (int i = 0; i < a.size() && i < b.size(); ++i)
	{
		if (a[i] != b[i])return a[i] < b[i];
	}
	return a.size() < b.size();
}
int main()
{
	cin >> n;
	search(0);
	sort(ans.begin(), ans.end(), cmp);
	int i = 0;
	for (vector<vector<int> >::iterator it1 = ans.begin(); it1 != ans.end(); it1++,i++)
	{
		if (!(i < 3))break;
		for (vector<int>::iterator it2 = it1->begin(); it2 != it1->end(); it2++)
		{
			cout << (*it2)+1 << " ";
		}
		cout << endl;
	}
	cout << tot;
}