TG1 基础数据结构 & P2070题解 & P3372题解
TG1 基础数据结构 & P2070题解 & P3372题解
约定：本文的下标从1开始，代码尽量从1开始（我在努力习惯），一般使用\(\LaTeX\)美化
这一节主要介绍了一些基础的数据结构 （废话），前缀和，差分，二分查找，离散化，ST表，线段树等。
来给大家一一介绍一下
前缀和
求解问题:
给你一个数组\(a\)，\(n\)次询问，每次输入\(l,r\),求\(\sum\limits_{i=l}^ra[i]\) (就是a[l...r]的和)。
基本思想:
计算数组\(b\)，对于每一个\(b[i]\),值就是\(\sum\limits_{j=1}^ia[j]\).
对于每次的l,r询问，答案就是\(b[r]-b[l-1]\).
问题来了：如何快速计算\(b?\)
for(int i = 1;i <= n;i++)
b[i] = a[i] + b[i-1];
我们只需要将前缀和累加即可。
如果我们不需要原来的\(a\)了，这样写代码可以减少内存的浪费 （别和我扯空间复杂度）,
\(\ \ \ \text{\color{red}注意,a[0]一定要=0！}\)
for(int i = 1;i <= n;i++)
a[i] += a[i-1];
差分
求解问题:
给定一个数组\(a\)，\(n\)次操作,每次给定\(l,r,v\),使区间a[l,r]都加上v.输出最后的数组
差分其实就是前缀和的逆运算（可以这样理解），计算差分和计算前缀和一样简单：
\[\\ \color{red}{\text{注意，像有损前缀和一样的，for语句要倒着写！}}\\
\color{black}
\text{为啥呢？请看下面这个：}\\
a={1,9,2,6,1,8,1,7}\\
\text{我们手玩是这样的（也就是无损的）}
b={1,8,-7,4,-5,7,-7,6}\\
\text{但是如果正着减的话，就会变成这样：}\\
a={1,8,-6,12,-12,20,-19,26}\\
\]
- 无损
for(int i = 1;i <= n;i++)
b[i] = a[i] - a[i-1];
- 有损
for(int i = n;i;i--)
b[i] -= b[i - 1];
二分查找
求解问题
求函数零点。
实现
upper_bound和lower_bound
非常的简单
离散化
求解问题
当数很大的时候，我们往往不能直接拿来存数组，这就是离散化的思想了。
实现
三部曲
- sort
- unique
- lower_bound 或者 upper_bound
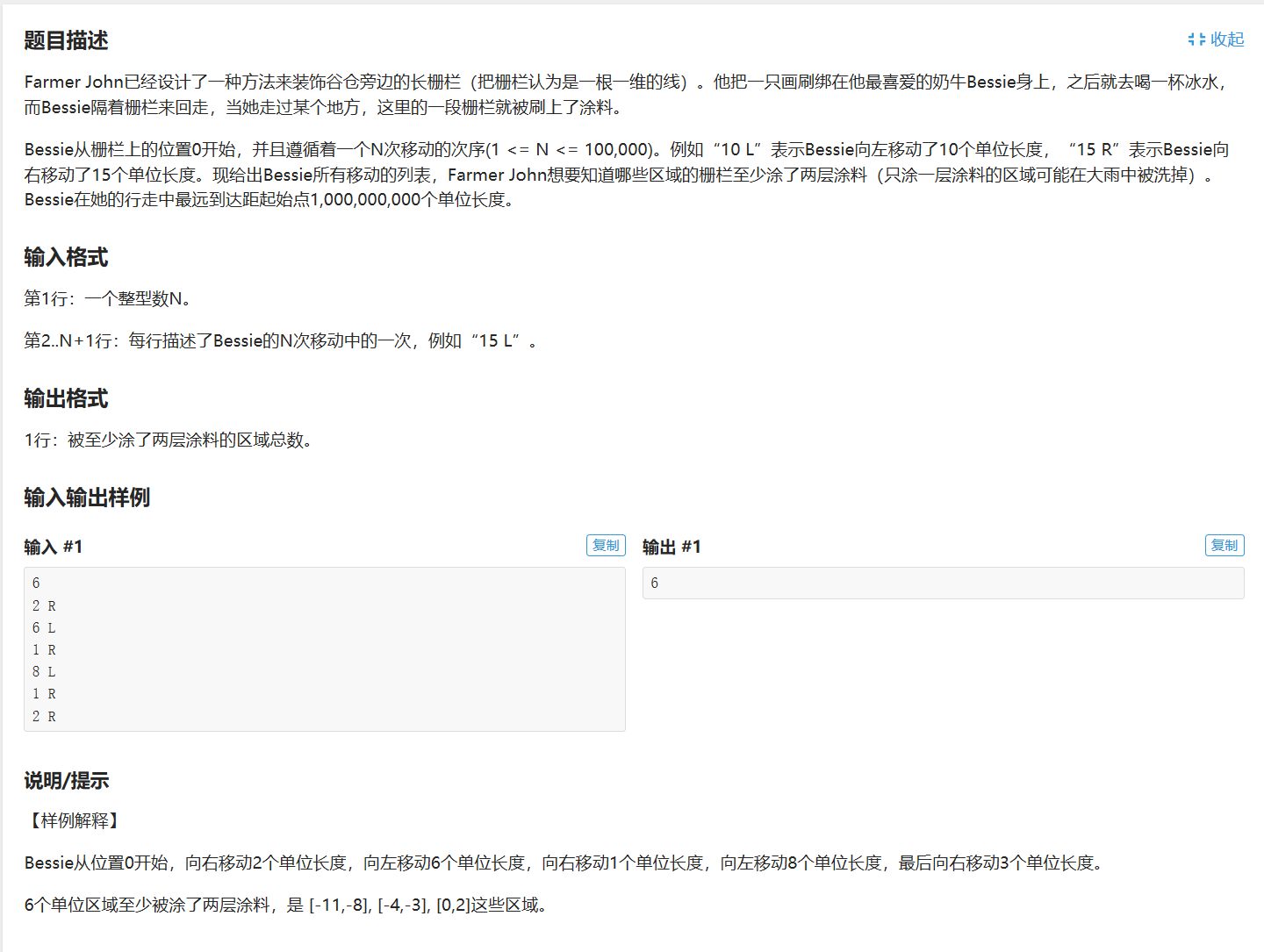
例题：
其实道理是非常简单的，唯一的问题就是数据范围非常的大，导致无法直接计算。怎么办？
这时就可以运用离散化的思想了。
但是，当我们再细细看题的时候： Bessie在她的行走中最远到达距起始点1,000,000,000个单位长度。
我的天！！！这个天才Bessie走这么远，我们要是乖乖开数组的话空间会不够的！！！这时我们又可以从什么方向入手呢？
我们回到我们一开始进行模拟的步骤，如果我们进行以下的移动的话会很简单： 3 R 2 L 3 R
0 1 2 3 4 1 2 2 2 1 （第一行是位置，第二行是经过次数）但如果变成这样会很麻烦： 1000000 R 500000 L 1000000 R More Actions。。。这个要是要写表格的话会死人的吧；但是这简单来写的话是不是这样呢？ 。。。这个要是要写表格的话会死人的吧；但是这简单来写的话是不是这样呢？ 0 1 2 3 -----------------------------------------------------------: ---: ---: ---: ---: 1 1 3 3
要是再简单点呢? 0 1 2 3 1 3 3 1
为了锻炼读者的代码阅读能力 （懒）,这个代码不添加任何注释。
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 2000010;
int a[maxn],b[maxn],c[maxn],n,sum,ans;
int o;char p;
void Paint(int ll,int rr)
{
int l = lower_bound(b,b+n+1,ll)-b;
int r = lower_bound(b,b+n+1,rr)-b;
if(l>r)swap(l,r);
c[l]++;c[r]--;
}
int main(void)
{
scanf("%d",&n);
for(int i = 1;i <= n;i++)
{
cin>>a[i]>>p;
if(p == 'L')a[i]=-a[i];
b[i] = b[i-1] + a[i];
}
sort(b,b+n+1);
int m = unique(b,b+n+1) - b;
for(int i = 1;i <= n;i++)
{
Paint(sum,sum+a[i]);
sum+=a[i];
}
sum = c[0];
for(int i = 1;i<m;i++)
{
if(sum > 1)ans+=b[i]-b[i-1];
sum+=c[i];
}
cout<<ans<<endl;
}
总结
离散化，说白了，就是把大数化小数的过程。
树状数组
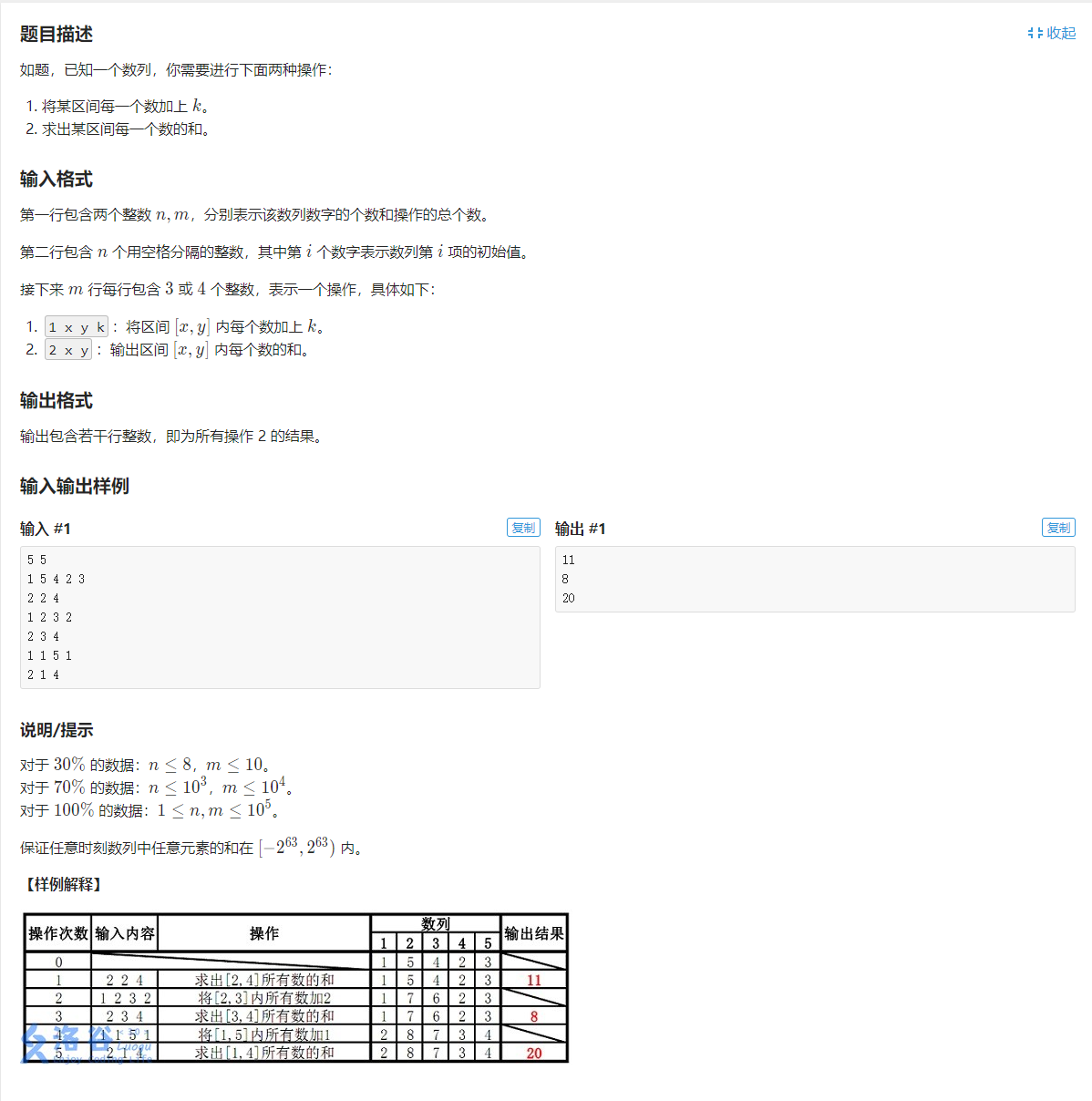
先看一道题:
\(\mathrm{Quz1:何为树状数组}\)？
就是没有右儿子的线段树。
处理的问题：
- 单点修改，区间查询（比较特殊，最小值：（只能查找左端点在1或者右端点在n的），和：无限制）
- 区间修改，单点查询（
基础差分技巧）
保存差分数组，利用差分技巧加减区间，单点查询就是查前缀和。 - 区间修改，区间查询（
高级差分技巧）
维护两个数组，一个\(tree1\)保存\(tree[i]\times (i-1)\)，一个正常保存差分。
答案就是：\((y \times ask(tree,y)-(x-1)\times ask(tree,x-1))-(ask(tree1,y)-ask(tree1,x-1))\)
具体的过程建议自己手推一下，加强记忆哦！
实现:
- lowbit
#define lowbit(n) (n&-n)
- 单点修改
void add(int pos,int val)
{
for(int i = pos;i <= n;i+=i&(-i))
tr[i]+=val;
}
int ask(int *tr,int m)
{
int ans=0;
for(int i = m;i>0;i-=i&(-i))
ans+=tr[i];
return ans;
}
- 区间
void add(int *tr,int pos,int val)
{
for(int i = pos;i <= n;i+=i&(-i))
tr[i]+=val;
}
void add_ran(int l,int r,int val)
{
add(t1,l,val);
add(t1,r+1,-val);
add(t2,l,val*(l-1));
add(t2,r+1,-val*r);
}
int ask(int *tr,int m)
{
int ans=0;
for(int i = m;i>0;i-=i&(-i))
ans+=tr[i];
return ans;
}
int sum(int r)
{
return r*ask(t1,r)-ask(t2,r);
}
int get_ran(int l,int r)
{
return sum(r)-sum(l-1);
}
这时候我们已经可以完美的解决问题了，就是：
//注意要开ll哦！
#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
const long long maxn = 100010;
long long n,m,t,l,r,val;//n个元素,m个询问.
long long a,b;
long long t1[maxn],t2[maxn];
void add(long long *tr,long long pos,long long val)
{
for(long long i = pos;i <= n;i+=i&(-i))
tr[i]+=val;
}
void add_ran(long long l,long long r,long long val)
{
add(t1,l,val);
add(t1,r+1,-val);
add(t2,l,val*(l-1));
add(t2,r+1,-val*r);
}
long long ask(long long *tr,long long m)
{
long long ans=0;
for(long long i = m;i>0;i-=i&(-i))
ans+=tr[i];
return ans;
}
long long sum(long long r)
{
return r*ask(t1,r)-ask(t2,r);
}
long long get_ran(long long l,long long r)
{
return sum(r)-sum(l-1);
}
int main(void)
{
scanf("%lld%lld",&n,&m);
for(long long i=1;i<=n;i++)
{
scanf("%lld",&a);
b=a-b;//差分.
add(t1,i,b);
add(t2,i,b*(i-1));
b=a;
}
for(long long i=1;i<=m;i++)
{
scanf("%lld",&t);
if(t == 1)
{
scanf("%lld%lld%lld",&l,&r,&val);
add_ran(l,r,val);
}
else
{
scanf("%lld%lld",&l,&r);
printf("%lld\n",get_ran(l,r));
}
}
return 0;
}
