LLM相关损失函数

信息熵：

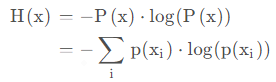
信息熵torch代码

event = {'a':2 , 'b':2, 'c':4}      # 信息熵分：1.5
event2 = {'a':1 , 'b':1, 'c':1}     # 信息熵分：1.585
p_e = [ v/sum(event.values()) for v in event.values() ]
en_e = [ item*torch.log2(torch.tensor(item)) for item in p_e ]
print(en_e)
info_entropy = -torch.sum(torch.tensor(en_e))

相对熵：KL散度

• KL：衡量两个分布的差异
• KL越大：分布差异大 / 拟合损失大 / 模型优化难度大
• KL(P||Q)通常不等于KL(Q||P)，概率分布一样，两者才会相等且为0。分别表示用分布 Q 拟合 P
• KL（ASR-wenet端到端识别中）：模型生成分布为（T,D,P）真实标签(T,D,1/n)
  

1维tensor计算

import torch.nn.functional as F
x = torch.tensor([0.5, 0.5])
y = torch.tensor([0.2, 0.8])
logp_x = torch.softmax(x, dim=-1)
p_y = torch.softmax(y, dim=-1)
kl_mean = F.kl_div(logp_x, p_y, reduction='mean')
kl_sum = F.kl_div(logp_x, p_y, reduction='sum')
kl_default = F.kl_div(logp_x, p_y )

d1 = [0.5, 0.5]
d2 = [0.2, 0.8]
d1 = torch.softmax( torch.tensor(d1), dim=-1 )
d2 = torch.softmax( torch.tensor(d2), dim=-1 )
def kl_self(d1, d2):
    return torch.tensor( [ d2[id]*(torch.log(d2[id])-v) for id, v in enumerate(d1) ] )
kl_self(logp_x, p_y).sum()

KL多维tensor计算（摘自wenet，与手写不一致可能是softmax部分）

d1 = [0.5, 0.5]
d2 = [0.2, 0.8]
kl = torch.nn.KLDivLoss(reduction="none")
kl( torch.tensor(d2) , torch.tensor(d1) )
# 手写
d1 = torch.softmax( torch.tensor(d1), dim=-1 )
d2 = torch.softmax( torch.tensor(d2), dim=-1 )
torch.tensor( [ d2[id]*(torch.log(d2[id])-v) for id, v in enumerate(d1) ] )

交叉熵：

def cross_entropy(t1, t2):
    return -[ t1[id]*torch.log(v) for id, v in enumerate(t2) ].sum()

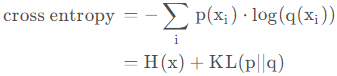
H(X)表示信息熵

可以坐下类似的下梯度推导工作
https://www.zhihu.com/tardis/zm/art/35709485?source_id=1003

为什么使用交叉熵而不是相对熵
计算简便性
交叉熵的计算公式相对简单,只需要目标值和预测值,而相对熵需要计算两个概率分布之间的距离,计算相对复杂。
监督学习场景
在监督学习中,我们有真实的目标值(标签),希望模型的预测值尽可能接近这个目标值。交叉熵可以很好地衡量预测值与目标值之间的差异,而相对熵主要用于衡量两个概率分布之间的差异。
优化目标
交叉熵的优化目标是最小化预测值与目标值之间的差异,这符合监督学习的目标。而相对熵的优化目标是使模型的概率分布尽可能逼近真实分布,在一些无监督学习场景下更有用。
梯度计算
在训练过程中,需要计算损失函数对模型参数的梯度。交叉熵损失函数的梯度计算相对简单,而相对熵涉及到复杂的对数运算,梯度计算更加复杂。
数值稳定性
相对熵的计算可能会遇到除以0或对数运算的数值不稳定的问题,而交叉熵损失函数通常数值更加稳定。